
высшая математика
.pdf
|
|
|
π |
|
|
|
π |
|
|
|
|
|
1 |
x |
2 |
|
sin t |
|
2 |
|
|
π |
|||
∫ |
dx = ∫ |
cos t dt = |
∫sin t dt = |
− cos t |
|
|
||||||
02 = 1 . |
||||||||||||
1− x 2 |
1− sin 2 t |
|||||||||||
0 |
0 |
|
|
0 |
|
|
|
|
||||
Подчеркнем два важных момента. Во-первых, при использовании формулы замены переменной (5) в интеграле справа следует найти и поставить новые пределы интегрирования. Во-вторых, в отличие от неопределенного интеграла, здесь нет необходимости возвращаться к старой переменной.
1
Пример 3. Найти интеграл ∫xe x dx .
0
Решение. Воспользуемся формулой интегрирования по частям:
1 |
1 |
|
|
10 |
1 |
1 |
∫xe x dx = ∫x dex = xe x |
− ∫ex dx = e − ∫ex dx = |
|||||
0 |
0 |
|
|
|
0 |
0 |
|
= e − ex |
|
1 = e − (e − 1) = 1 . |
|
||
|
|
|
||||
|
|
|
0 |
|
|
|
|
|
|
|
|
||
!Задания для самостоятельной работы
1.Вычислить интегралы:
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
1 |
|
|
8 |
|
|
|
|
|
4 |
|
|
|
|
|
а) |
∫(x 2 + |
2x − |
3) dx ; б) ∫( |
2x + 3 |
x ) dx ; |
в) |
|
∫sin |
2 |
ϕ dϕ . |
|||||
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
2. |
Вычислить интегралы: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
ln 2 |
|
|
π |
|
|
1 |
|
|
|
|
|
|
|
|
а) |
∫xe |
− x dx ; |
б) ∫x 2 sin x dx ; |
в) |
∫arcsin x dx . |
|
|
|
|||||||
|
0 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
3. |
Вычислить интегралы: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
x |
|
3 4 |
dx |
|
|
π |
|
|
dx |
|
|
|
|
а) ∫ |
dx ; б) ∫ |
|
; в) |
∫ |
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
− 1 5 |
− |
4x |
0 (x + |
1) |
x 2 |
+ 1 |
0 3 |
+ 2 cos x |
||||||
2 4 1
|
Лекция 39 |
|
|
|
|
|
|
|
Приложения |
определенного интеграла |
|
в геометрии |
и экономике |
|
Приведены формулы для вычисления площади некоторых фигур, длины дуги кривой, объема тела вращения. Рассматриваются некоторые применения определенного интеграла в экономике.
10. Площадь криволинейной трапеции. В |
лекции 37 |
b |
|
уже отмечалось, что определенный интеграл ∫ f (x ) dx |
от неотрица- |
a
тельной функции f численно равен площади криволинейной трапеции, ограниченной графиком функции у = f (x), прямыми х = а, х = b и у = 0.
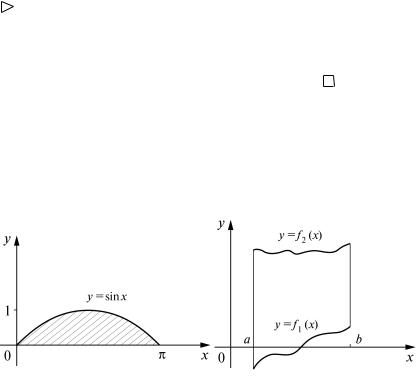
Пример 1. Вычислить площадь фигуры, заключенной между
осью Ox и синусоидой y = sin x, |
x |
[0; π ] (рис. 1). |
||
Решение. Имеем |
|
|
||
π |
|
|
||
S = ∫sin x dx = − cos x |
|
0π |
= |
− (cos π − cos 0) = 2 . |
|
||||
0 |
|
|
|
|
Если фигура не является криволинейной трапецией, то ее площадь стараются представить в виде суммы или разности площадей фигур, являющихся криволинейными трапециями. В частности, если фигура ограничена снизу и сверху графиками непрерывных функций у = f1(x), у = f2(x) (не обязательно неотрицательных, рис. 2), то
Рис. 1 |
Рис. 2 |
2 4 2

b |
b |
S = ∫ f2 (x ) dx − ∫ f1 (x ) dx . |
|
a |
a |
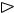 Пример 2. Вычислить площадь фигуры, ограниченной кривой ху = 4 и прямыми у = х и х = 4.
Пример 2. Вычислить площадь фигуры, ограниченной кривой ху = 4 и прямыми у = х и х = 4.
Решение. Построим фигуру на плоскости (рис. 3). Очевидно,
f |
1 |
(x) |
= |
|
4 |
, f (x) = x, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||||
|
|
|
|
x |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4 |
|
|
|
4 |
|
|
x 2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||
S = ∫ |
x − |
|
dx = |
|
|
− |
|
|
= |
|||||
x |
|
2 |
4 ln x |
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|
|||||
|
= 8 – 4 ln 4 – (2 – 4 ln 2) = |
Рис. 3 |
= 2 (3 – 2 ln 2). |
|
20. Длина дуги кривой. Вычисление длин кривых также приводит к интегралам. Пусть функция у = f (x) непрерывна на отрезке [a; b] и дифференцируема на интервале (a; b). Ее график представляет некоторую кривую АВ, A(a; f (a)), B(b; f (b)) (рис. 4). Кривую АВ разобьем точками C0 = A, C1, C2 , ..., Cn = B на n произвольных частей. Соединим две соседние точки Ck-1 и Ck хордами, k = 1, 2, ..., n. Получим n-звенную ломаную, вписанную в кривую АВ. Пусть lk есть длина хорды Ck-1Ck ,
k = 1, 2, ..., n, |
ω = max lk . Длина ломаной будет выражаться формулой |
||||
|
1≤ k ≤ n |
|
|
|
|
|
|
Ln = ∑n |
lk . |
|
|
|
|
k = 1 |
|
|
|
Естественно определить длину L кривой АВ как предельное зна- |
|||||
чение длин ломаных Ln, |
когда ω → |
0, т.е. |
|
||
|
L |
= lim Ln = |
lim ∑n |
lk . |
(1) |
|
|
ω → 0 |
ω → 0 k = 1 |
|
|
Пусть xk |
есть абсциссы точек Ck , k = 1, |
2, ... , n, |
|||
|
a = x0 < x1 < x2 < ... < xk-1 < xk < ... < xn = b. |
||||
Тогда координаты точек Ck есть (xk ; f (xk)), и, пользуясь формулой для расстояния между двумя точками (см. Л. 2), найдем
lk = (x k − x k − 1 )2 + ( f (x k ) − f (x k − 1 ))2 . |
(2) |
2 4 3
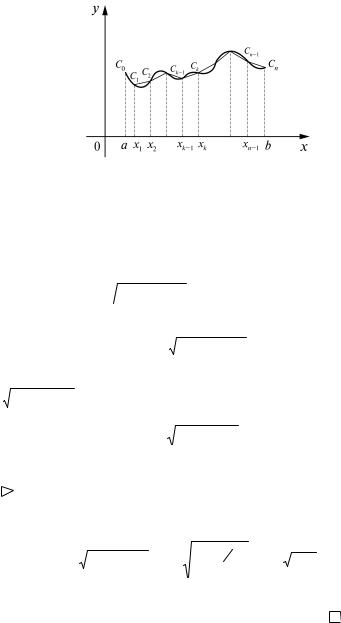
Рис. 4
По формуле конечных приращений имеем:
f (x k ) − f (x k − 1 ) = f ′(ξ k )(x k − x k − 1 ), ξ k (x k − 1; x k ) .
Подставляя полученное выражение в (2), найдем:
lk =  1+ ( f ′(ξ k ))2 ∆x k , ∆x k = x k − x k − 1 ,
1+ ( f ′(ξ k ))2 ∆x k , ∆x k = x k − x k − 1 ,
и
Ln = ∑n |
1 + ( f ′(ξ k )) 2 ∆ xk . |
k = |
1 |
Следовательно, Ln есть |
интегральная сумма для функции |
1+ ( f ′(x ))2 на отрезке [a; b]. |
Тогда на основании равенств (1) имеем: |
|
|
|
|
|
|
b |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
L = ∫ |
1+ ( f |
|
2 |
dx . |
|
|
|
|
(3) |
||||||||||||||
|
|
|
|
(x )) |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
Пример 3. Найти длину графика |
|
y = |
|
x |
2 |
|
|
между х = 0 и х = 3. |
|||||||||||||||||||
|
3 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. По формуле (3) находим: |
|
|
|
|
|
|
|
||||||||||||||||||||
3 |
1+ |
( y′(x )) |
2 |
dx |
= |
3 |
|
12 |
|
2 |
|
|
|
3 |
|
|
|
|
|
||||||||
L = ∫ |
|
∫ 1+ |
x |
|
|
|
dx = |
∫ 1+ x dx = |
|||||||||||||||||||
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||
3 |
|
1 |
|
|
|
|
2 |
|
3 |
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
14 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= ∫(x + 1) |
|
d(x + 1) = |
|
(x + |
1) |
|
|
|
= |
|
(8 − 1) |
= |
|
. |
|||||||||||||
2 |
|
2 |
|
|
|||||||||||||||||||||||
|
3 |
|
|
3 |
3 |
||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 4 4
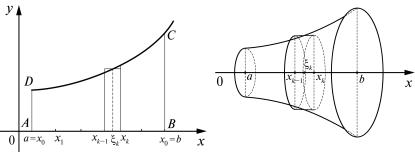
а) |
б) |
Рис. 5
30. Объем тела вращения. Пусть функция f непрерывна и неотрицательна на отрезке [a; b]. Построим соответствующую криволинейную трапецию АВСD (рис. 5а).
Если криволинейную трапецию АВСD вращать вокруг оси Ox, то образуется тело, называемое телом вращения (рис. 5б). Поставим задачу определения и вычисления объема V этого тела.
С этой целью разобьем отрезок [a; b] точками:
a = x0 < x1 < ... < xn = b, ∆ xk = xk – xk-1 |
, λ = max ∆x k . |
|
1≤ k ≤ n |
Произвольно выберем по точке ξ k [xk–1; x k] , вычислим f (ξ k), k = 1, |
|
2, ... , n. Теперь построим плоскости, проходящие через каждую точку
xk и перпендикулярные оси Ox. Они разобьют тело на n частей (элементарных тел). Каждое элементарное тело заменим цилиндром с радиусом f (ξ k) и высотой ∆ xk. Объем такого цилиндра равен π (f (ξ k))2 ∆xk, и естественно полагать, что объем тела
V = ∑n π ( f (ξ k ))2 ∆x k .
k = 1
В правой части этого равенства стоит интегральная сумма для функции π f 2(x) на отрезке [a; b]. Поэтому, переходя к пределу при λ → 0, найдем
b |
|
V = π ∫ f 2 (x ) dx . |
(4) |
a
Таким образом, формула (4) есть формула для вычисления объемов тел вращения вокруг оси Ox криволинейной трапеции, ограниченной графиком функции у = f (x) и прямыми х = а, х = b, у = 0.
2 4 5

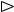 Пример 4. Найти объем тела, полученного вращением вокруг оси Ox области под параболой y = x2 от x = 0 до x = 2.
Пример 4. Найти объем тела, полученного вращением вокруг оси Ox области под параболой y = x2 от x = 0 до x = 2.
Решение. По формуле (4) имеем
|
2 |
x |
5 |
|
|
2 |
32 |
|
|
|
|
|
|
|
|
||||||
|
V = π ∫x 4 dx = π |
|
|
|
= |
|
π . |
|
||
|
5 |
5 |
|
|
||||||
|
0 |
|
|
0 |
|
|
|
|||
40. |
|
|
|
|
|
|
|
|||
Использование |
|
|
|
|
понятия |
определенного |
||||
интеграла в экономике. Рассмотрим |
сначала экономичес- |
|||||||||
кий смысл определенного интеграла. |
|
|
||||||||
Пусть функция u = f (t) описывает изменение производительности некоторого завода с течением времени. Найдем объем продукции u, произведенной за промежуток времени [0; T].
Если предположить, что производительность не изменяется с течением времени (т.е. f (t) = const), то объем продукции ∆u, произведенной за некоторый промежуток времени [t; t+∆t], задается формулой ∆ u = f (t)∆t . Если f (t) не является постоянной функцией, то справедливо приближенное равенство ∆u ≈ f (ξ )∆t, где ξ [t; t+∆t], которое оказывается тем точнее, чем меньше ∆t.
Поэтому для решения задачи о нахождении объема продукции поступим так же, как при нахождении площади криволинейной трапеции. Разобъем отрезок [0; T ] на промежутки времени точками:
0 = t0 < t1 < t2 < ... < tn = T.
Для величины объема продукции ∆ui , произведенной за проме-
жуток времени |
[ti − 1; ti ], i = |
|
1, n |
, имеем: |
|
∆ui ≈ |
f (ξ i )∆ti , |
где |
ξ i |
[ti − 1; ti ], ∆ti = ti − ti− 1 . |
|
Тогда |
|
|
|
|
|
|
u ≈ ∑n ∆ui = ∑n |
f (ξ i )∆ti . |
|||
|
i = |
1 |
|
i= |
1 |
При стремлении max ∆ ti к нулю каждое из использованных при- |
|||||||
i |
|
|
|
|
|
|
|
ближенных равенств становится все более точным, поэтому |
|||||||
u = |
lim |
n |
f (ξ |
|
)∆t |
|
|
0 ∑ |
i |
i . |
|||||
max ∆ ti → |
|
|
|||||
i |
|
i = 1 |
|
|
|
|
|
Учитывая определение определенного интеграла, окончательно |
|||||||
T |
|
|
|
|
|
|
|
получаем u = ∫ f (t)dt , т.е. |
если f (t) |
– |
производительность труда в |
||||
0 |
|
|
|
|
|
|
|
2 4 6

T
момент времени t, то ∫ f (t)dt есть объем выпускаемой продукции за
0
промежуток [0; T ].
Сравнивая данную задачу с задачей нахождения площади криволинейной трапеции, получаем, что величина объема продукции, произведенной за промежуток времени [0; T ], численно равна площади фигуры, ограниченной графиком функции u = f (t), описывающей изменения производительности труда с течением времени, отрезком [0; T ] и прямыми t = 0, t = T.
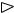 Пример 5. Определить объем продукции, произведенной рабочим за второй час рабочего дня, если производительность труда ха-
Пример 5. Определить объем продукции, произведенной рабочим за второй час рабочего дня, если производительность труда ха-
рактеризуется функцией f (t) = 2 + 3 . 3t + 4
Решение:
|
2 |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
V = ∫ |
|
|
|
+ |
3 dt = |
|
|
ln |
3t + |
4 |
+ |
3t |
|
= |
||||||||
3t + |
4 |
3 |
||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
2 |
ln10 − |
|
2 |
ln 7 + |
6 − |
|
3 = |
2 |
ln |
10 |
+ |
3 . |
|
|
|||||||
|
3 |
|
3 |
|
|
|
||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|||||||
В экономических исследованиях часто используется производ- |
||||||||||||||||||||||
ственная функция Кобба-Дугласа |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
y = |
a x a1 x a2 |
, |
|
|
|
|
|
(5) |
||||||
|
|
|
|
|
|
|
|
|
0 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
где y – величина общественного продукта; x1 – затраты труда, x2 – объем производственных фондов.
Если в (5) затраты труда есть линейная зависимость от времени, а затраты капитала неизменны, то функцию Кобба-Дугласа можно преобразовать к виду
g(t) = (αt + β) eγt.
Тогда объем выпускаемой продукции за Т лет составит:
T |
|
Q = ∫(αt + β) eγt dt . |
(6) |
0 |
|
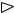 Пример 6. Найти объем продукции, произведенной за 4 года, если функция Кобба-Дугласа имеет вид g(t) = (1+t) e3t.
Пример 6. Найти объем продукции, произведенной за 4 года, если функция Кобба-Дугласа имеет вид g(t) = (1+t) e3t.
2 4 7

Решение. По формуле (6) объем Q произведенной продукции равен
|
|
4 |
|
|
|
e |
3t |
|
|
4 |
4 |
1 e3t dt = |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||
|
|
Q = ∫(1+ t) e3t dt = |
|
(t + 1) |
|
− ∫ |
||||||
|
|
3 |
||||||||||
|
|
0 |
|
|
|
|
|
0 |
0 |
3 |
||
|
1 |
(5e12 − 1) − |
1 e3t |
|
4 |
1 (14e12 − 2) ≈ |
2,53 105 . |
|||||
|
|
|||||||||||
= |
|
= |
||||||||||
|
3 |
|
9 |
|
0 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для вычисления интеграла здесь использован метод интегрирования по частям, т.е. u = t + 1, dv = e3tdt , тогда
|
|
|
du = dt, |
v = |
1 e3t . |
|
|
|
|
|
3 |
Часто для решения экономических задач применяют теорему о |
|||||
среднем значении и формулу |
|
|
|||
b |
|
|
|
|
|
∫ f (x ) dx = f (ξ )(b − |
a), |
где ξ [a; b] . |
|||
a |
|
|
|
|
|
|
1 |
|
b |
|
|
Число f (ξ ) = |
|
∫ f (x ) dx |
называют средним значением функ- |
||
b − |
|
||||
|
a a |
|
|
||
ции f (x) на отрезке [a; b].
На практике нередко вычисляют такого рода средние значения, например, средняя производительность труда, средняя мощность электродвигателей и т.д.
Пусть известна функция t = t (x), описывающая изменение затрат времени t на изготовление изделия в зависимости от степени освоения производства, где x – порядковый номер изделия в партии. Тогда среднее время tср, затраченное на изготовление одного изделия в период освоения от x1 до x2 изделий, вычисляется по теореме о среднем
|
|
|
1 |
|
x 2 |
tср |
= |
|
|
∫t(x ) dx . |
|
x2 |
− |
|
|||
|
|
x1 x1 |
|||
Что касается функции изменения затрат времени на изготовление изделий t = t(x), то она часто имеет вид:
t = Ax–B, |
(7) |
где А – затраты времени на первое изделие, В – показатель производственного процесса.
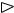 Пример 7. Найти среднее значение издержек K (x) = 3x2 + 4x + 1, выраженных в денежных единицах, если объем продукции x меняется
Пример 7. Найти среднее значение издержек K (x) = 3x2 + 4x + 1, выраженных в денежных единицах, если объем продукции x меняется
2 4 8

от 0 до 3 единиц. Указать объем продукции, при котором издержки принимают среднее значение.
Решение. Применяя теорему о среднем значении, имеем:
|
1 |
3 |
|
2 |
|
|
|
1 |
|
x 3 |
|
|
x 2 |
|
|
|
3 |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
f (ξ ) = |
|
∫(3x |
|
|
+ 4x + 1) dx |
= |
|
|
|
3 |
|
+ |
4 |
|
+ |
x |
|
= |
|
3 |
|
|
|
3 |
2 |
||||||||||||||
|
0 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
0 |
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= |
(27 + 18 + 3) = |
|
16 (ден. ед.) , |
|
|
|
|
||||||||||
|
|
3 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.е. среднее значение издержек равно 16.
Определим, при каком объеме продукции издержки принимают это среднее значение, т.е. решим уравнение
3x2 + 4x + 1 = 16.
Учитывая, что объем продукции не может быть отрицательным,
из последнего уравнения имеем x = 53 (ед. продукции). 
Определение начальной суммы по ее конечной величине, полученной через время t (лет) при годовом проценте (процентной ставке) p, называется дисконтированием. Задачи такого рода встречаются при определении экономической эффективности капитальных вложений.
Пусть Kt – конечная сумма, полученная за t лет, и К – дисконтируемая (начальная) сумма, которую в финансовом анализе называют также современной суммой. Если проценты простые, то Kt = K (1 + i t),
где i = |
|
p |
– удельная процентная ставка. Тогда |
K |
= |
|
Kt |
|
. В случае |
||
100 |
|
|
|
|
|||||||
|
|
|
|
|
|
1+ it |
|||||
сложных процентов Kt = K (1+ it)t и поэтому K = |
|
|
Kt |
|
. |
|
|||||
(1 |
+ |
it)t |
|
||||||||
|
|
|
|
|
|
||||||
Пусть поступающий ежегодно доход изменяется во времени и описывается функцией f (t), и при удельной норме процента, равной i, процент начисляется непрерывно. В этом случае дисконтированный доход К за время Т вычисляется по формуле:
T |
|
K = ∫ f (t) e− i t dt . |
(8) |
0 |
|
 Пример 8. Определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10 тыс. условных единиц и намечается ежегодное увеличение капиталовложения на 1 тыс. у.е.
Пример 8. Определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10 тыс. условных единиц и намечается ежегодное увеличение капиталовложения на 1 тыс. у.е.
2 4 9
Решение. Очевидно, что капиталовложения задаются функцией f (t) = 10 + 1 t = 10 + t. Тогда по формуле (8) дисконтируемая сумма
3
капиталовложений K = ∫(10 + t) e− 0,08t dt .
0
Применяя формулу интегрирования по частям, получим К = 30,5 тыс. усл. единиц.
Это означает, что для получения одинаковой наращиваемой суммы через три года ежегодные капиталовложения от 10 до 13 тыс. у. е. равносильны одновременным первоначальным вложениям 30,5 тыс. у. е. при той же начисляемой непрерывно процентной ставке.
!Задания для самостоятельной работы
1.Вычислить площадь фигуры, ограниченной графиком функ-
ции y = 3 x и прямыми х = 0, у = 1.
2. |
Вычислить площадь фигуры, ограниченной графиками сле- |
||||||||||||
дующих функций: |
|
|
|
|
|
|
|
|
|||||
a) y = x2 |
, y = x + 2; |
|
б) y = – x2 , y = x4 – 20; |
||||||||||
в) |
y = |
|
1 |
, y = |
x 2 |
. |
|
|
|
|
|
|
|
|
1 |
+ x 2 |
|
2 |
|
|
|
|
|
|
|
||
3. |
Вычислить длину параболы y = |
2 x от x = 0 до x = 1. |
|||||||||||
4. |
Вычислить длину дуги кривой y = ln cos x, 0 ≤ x ≤ |
π |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
||
5. |
Найти объем тела, образованного вращением вокруг оси Ox |
||||||||||||
области под графиком функции |
y = |
1 |
|
от x = 1 до x = e. |
|||||||||
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
6. |
Найти объем тела, образованного вращением вокруг оси Ox |
||||||||||||
области, ограниченной кривыми |
y = |
x , x = 0 и y = 1. |
|||||||||||
7. |
Найти объем тела, образованного вращением вокруг оси Oy |
||||||||||||
области под графиком y = 1 – x2 |
от х = 0 до х = 1. |
||||||||||||
8. Найти полные издержки производства, если объем продукции равен 42 единицам, а зависимость издержек от объема имеет вид:
K(x) = x3 – 2x2 + x.
2 5 0
