высшая математика

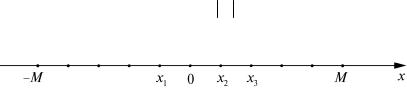
тельность xn

называется ограниченной, если M > 0 такое, что

Рис. 1

Например:

а)

последовательность 1, −

1

,

1

,$,

(− 1)n− 1

,$

ограничена,

2

3

n

так как

n

N :

x n

=

1

≤

1 ;

n

б) последовательность 1, 22, 32,..., n2,.. является неограниченной,

так как каково бы ни было число M > 0

xn = n2 такое, что xn > M.

20.

Бесконечно

малые

и

бесконечно

большие

сколько угодно малое оно ни было, N0

N такое, что все члены последо-

вательности,

начиная

c

(N0 + 1)-го,

принадлежат

Доказательство. Достаточно получить свойство для суммы

двух БМП. Пусть xn

и yn

есть БМП. Зададим произвольное число

ε> 0. В соответствии с определением БМП для числа

ε

существуют

2

ε

ε

номера N1

и N2 такие,

что

n > N1 : xn

<

и

n > N2 : yn <

.

N0 = max N1,N2 .Тогда

2

2

Полагаем

n > N0

будем иметь, что

x

+ y

≤ x + y <

ε

+

ε

= ε. Таким образом,

ε> 0 N

N, т.е.

2

n

n

n

n

2

0

такой, что

n > N0 : xn + yn < ε. По определению это означает, что

последовательность

xn + yn

есть БМП.

Приведем другие свойства БМП.

5. Если БМП xn имеет постоянное значение a, т.е. n

N : xn = a,

то a = 0.

Последовательность xn называется бесконечно

большой

(ББП), если A > 0 N0 N такой, что n > N0 : xn > A.

Теорема.

30. Сходящиеся

последовательности.

Число а называется пределом последовательности xn , если

ε> 0 N0 N такой, что

n > N0 : xn – a < ε.

xn

, a = 0.

=

∞ .

Если последовательность x

есть ББП,

то пишут lim x

n

n→

∞

n

Приведем основные свойства сходящихся последовательностей.

1. Для того, чтобы последовательность xn

имела своим преде-

лом число а, необходимо и достаточно, чтобы последовательность

xn

– a

была БМП.

Доказательство. Необходимость.

Пусть a = lim xn . Тогда

ε> 0 N0 N, т.е. такой, что n > N0 : xn – a <

n→

∞

ε. Это означает, что

последовательность xn

– a

есть БМП.

Достаточность. Пусть последовательность xn – a

есть БМП.

Тогда

ε> 0 N0 N,

т.е. такой,

что n > N0 : xn – a < ε. Это озна-

чает, что последовательность xn

сходится к а.

2. Сходящаяся последовательность имеет только один предел.

Доказательство.

Предположим противное. Пусть

a = lim xn ,

b =

, a ≠ b. Тогда последовательности

– a и

x

n→

∞

lim x

n

x

n

n

– b

есть

n→ ∞

n и

БМП.

Обозначим xn – a = α n,

xn – b = β n. Последовательности α

β n –

БМП. Имеем

xn = a +α n,

xn = b + β n. Отсюда получим,

что

a + α

n = b + β n и a – b = β n–α n. Так как β n – α n

есть БМП, то в соответ-

ствии со свойством 5 БМП имеем b – a = 0,

т.е. b = a.

3. Сходящаяся последовательность ограничена.

Действительно, пусть

{xn }–

сходящаяся последовательность,

a =

lim x

n

. Зададим произвольное число ε> 0.

Пусть N

0

– номер, на-

n→ ∞

чиная

с

которого выполняется

неравенство

xn – a < ε. Тогда

n > N0 : xn = (xn – a) + a ≤ xn – a + a < a + ε.

Пусть M = max {

a

+ ε,

x1

, $,

x N 0

}. Тогда

n N : xn≤ M.

Значит, последовательность

{x

n } ограничена.

Свойство 3

4. Пусть

lim xn =

a

и lim yn =

b .

n→ ∞

n→ ∞

Тогда:

a)

lim(xn ± yn ) =

a ± b ;

n→ ∞

б)

lim xn yn = ab ;

n→

∞

в)

lim

xn

=

a

( при условии, что b ≠ 0).

yn

b

Докажем,

n→ ∞

что

lim(x n + yn ) =

a + b . Действительно,

из

например,

того, что lim xn =

и

lim yn =

n→ ∞

следует:

xn – a = α n, yn – b = β n,

где

a

b

n→ ∞

n→

∞

тельности, доказать, что

lim

n

=

1

.

2n − 1

2

n→ ∞

Решение. Зададим произвольное

ε> 0 и рассмотрим модуль

разности между n-ым членом последовательности и числом

1

:

2

2n − (2n − 1)

n

1

=

1

−

=

.

2n − 1

2

2(2n − 1)

2(2n − 1)

ство

1

< ε .

2(2n − 1)

2 (2n −

1) >

1

1

1

n >

+

1 .

ε

2

2ε

1

1

1

1

числа

+

1 , т.е.

N 0 =

+

1 .

2

2ε

2ε

2

1

1

1

1

2n

2

+ n +

2

+

+

lim

2 +

+

1

n

n

2

n

n2

lim

= lim

=

n→

∞

=

n2 − 1

1

1

n→ ∞

n→

∞

1−

lim 1

−

n2

n→

∞

n2

lim 2 +

lim

1

+

lim

1

2 + 0 + 0

n2

=

n→

∞

n→

∞

n

n

→ ∞

=

=

2 .

lim1−

lim

1

1−

0

n2

n→

∞

n→

∞

! Задания для самостоятельной работы

1. Ограничены ли последовательности:

а)

x n =

2 +

(− 1)n

; б)

xn

=

sin(n) ;

в)

xn =

n ; г)

xn

=

ln(n) ?

n

2. Пользуясь определением предела последовательности,

докажите, что:

а)

lim

1

=

0 ; б)

lim

n

=

1 ; в)

lim

cos n

=

0 .

n→ ∞

n2

n→

∞

n

+

2

n

→

∞

n

3.

Найти пределы:

а)

lim

(2n − 1)( n + 2)

;

б)

lim

(n + 1)

2

;

в)

lim

n +

(− 1)n

.

n2 + n +

1

n2 +

n

−

(−

1)n

n→ ∞

n→

∞

n

n→

∞

г)

lim

2n+ 1 +

3n+ 1

;

д)

lim(

n +

1 −

n);

2n + 3n

n→ ∞

n→

∞

4.

Пусть

последовательность

xn

+ yn

сходится. Следует ли

отсюда, что последовательности

xn ,

yn сходятся?

10. Предельный переход в неравенствах.

Теорема

1.

Если

lim xn = a и, начиная с некоторого номера, xn ≥ b, то а ≥ b.

n→ ∞

Доказательство. Предположим противное, пусть a < b. Тогда

возьмем ε= b – a.

По определению предела последовательности для

данного числа

ε > 0

N0 N такой, что

n > N0 : |xn – a| < ε,

т.е.

|xn – a| < b – a или – (b – a) < xn

– a < b – a. Из

правого неравенства

получаем:

n > N0 : xn < b, что противоречит условию теоремы.

{xn }

Следствие. Если элементы сходящихся последовательностей

и {yn },

начиная с некоторого номера, удовлетворяют неравенству

xn ≤

yn, то и их пределы удовлетворяют неравенству

lim xn

= lim yn .

n→ ∞

n→ ∞

Действительно, начиная с некоторого номера, будем иметь, что

yn −

xn ≥

0 .

Следовательно,

по

теореме

1

lim(yn − xn ) ≥

0

и

lim yn −

lim xn ≥ 0

. Теорема доказана.

n→ ∞

n→ ∞

n→ ∞

С помощью настоящего следствия можно доказать следующую

теорему.

Теорема 2 (о сжатой последовательности).

Пусть даны три

последовательности

{xn }, {yn }, {zn } и,

начи-

ная с некоторого номера xn ≤ yn ≤ zn,

пусть последовательности

{xn }

и {yn } имеют один и тот же предел а. Тогда последовательность

{yn} также имеет предел а.

2

0. Монотонные последовательности. Последователь-

ность

{xn }

называется неубывающей, если

n

N : xn ≤ xn+1, невозрас-

тающей, если

n N : xn+1 ≤ xn.

ся монотонными.

, то последовательность {xn } называется

Если

n N : xn < xn+1

возрастающей,

если же n

N : xn+1 < xn, то убывающей. Возрастающие

а)

0,

1

,

2

,$,

n − 1

,$ –

возрастающая

ограниченная после-

2

3

n

n − 1

довательность.

Очевидно, она сходится,

lim

= 1.

n

n→ ∞

б)

2, 4, 8,..., 2n,...

– возрастающая неограниченная последо-

вательность. Эта последовательность является ББП.

в)

1,

3

,$,sin

n

1

π ,$ – убывающая ограниченная последо-

2

n +

вательность,

n

π

π

lim sin

π

= lim sin π −

= lim sin

= 0 .

n

+

1

n + 1

n +

1

n→

∞

n→ ∞

n→

∞

довательности является последовательность {xn }, где

1

n

x n =

1

+

. По-

n

xn

= 1+ n

1

+

n(n − 1) 1

+

n(n − 1)( n − 2) 1

+

n

2! n2

3!

n3

+ $+

n(n − 1)( n − 2) $(n −( n − )1 )

1

.

n!

nn

Преобразуем полученное выражение следующим образом:

x n =

+

1

−

1

+

1

1−

1

2

1

1

2

n −

1

2

1

1−

+ … +

1−

1

−

$

1

−

.

(1)

2!

3!

n

n

n

n

n!

n

n

1

1

1

1

2

xn+ 1 = 2 +

1

−

+

1

−

1−

+

3!

n +

2!

n + 1

n + 1

1

1

1

2

n

− 1

+ $+

1−

1

−

$ 1−

+

n +

n +

1

n!

1

n + 1

1

1

2

n

+

1−

1

−

$ 1−

.

(n +

n +

n + 1

n + 1

1)!

1

Сравним члены последовательности xn и xn+1. Очевидно, что

1−

k

< 1−

k

, k = 1,2,$, n − 1 . Поэтому первые n

слагаемых x

не

n +

n+1

n

1

n N : xn

< xn+1.

что

рассматриваемая

последовательность

Далее

докажем,

1

n

+

1

ограничена.

Снова воспользуемся формулой (1).

Очевид-

n

но,

имеет место неравенство 2n–1 < n!, n = 3, 4,... .

Поэтому из соотношения (1) будем иметь:

1

1

1

1

1

1

xn < 2 +

+

+ $+

< 1

+ 1+

2 +

+

$+

.

2!

3!

n!

22

2n− 1

Применим формулу суммы геометрической прогрессии

1−

1

1

xn <

1+

2n

= 3 −

< 3,

n

N .

(2)

2n− 1

1−

1

2

1

n

+

Следовательно, последовательность

1

возрастающая и

n

буквой е, e =

+

1

n

lim 1

.

n→ ∞

n

20. Теорема о вложенных отрезках.