Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

высшая математика

.pdf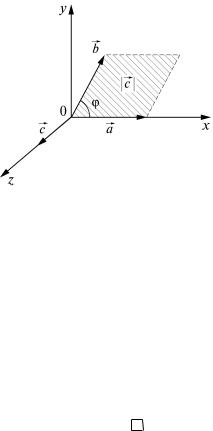

Скачиваний:

Добавлен:

18.02.2016

Размер:

5.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 418 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Рис. 1

Пример 2. Выразить модуль векторного произведения ненулевых векторов через угол между векторами.

	Решение. Выберем
!	= col (a; 0; 0), a =	!	,
a		a

(рис. 1).

Используя формулу

систему координат таким образом, чтобы
!	col (b cos ϕ ; b sin ϕ ; 0), b =	!	, 0	≤ ϕ ≤ π
b =		b
(2),	получаем:

×b

b cos ϕ

bsin ϕ

kabsin ϕ .

b cos ϕ

b sin ϕ

Отсюда

= absin ϕ

S .

×b

Итак, имеет место свойство, раскрывающее геометрический смысл векторного произведения:

d) Модуль векторного произведения равен площади параллелограмма, построенного на этих векторах.

30. Смешанное произведение векторов.

Смешанным произведением трех упорядоченных векторов называется скалярное произведение одного из векторов на векторное произведение двух других.

Представим смешанное произведение векторов a = col (ax ;ay ; az ),

= col (b

;b )

c! = col (c

)

в виде определителя. Имеем

! !

a ×b

= i (a

×b)x +

j(a

×b) y +

×b) z , следовательно:

7 1

cy(

y +

, a

×b) =

cx(a ×b) x

×b)

c(z a

×)b z =

−

(3)

40. Свойства смешанного произведения.

Компланарными называют векторы, лежащие в одной плоскости.

а )

Смешанное произведение компланарных векторов равно нулю.

лежит в той же плоскости, что и

Действительно, если c

, и b ,

то

= λ

1a + λ 2b .

(c, a ×b) =

λ 1ax + λ 2bx

λ 1ay + λ 2by

λ 1az + λ 2bz

= 0

Тогда

по свойству определителя. b1) Четная перестановка

его не меняет, т.е.

(! [! !)]= (! c, a,b a,

Соотношение (4) вытекает

векторов в смешанном произведении

! !	! ! !	(4)
[b,c )]=	(b,[c, a )].	(4)

из известного свойства определителя:

cx	cy	cz		ax	ay	az		bx	by	bz
ax	ay	az	=	bx	by	bz	=	cx	cy	cz
bx	by	bz		cx	cy	cz		ax	ay	az

(четная перестановка строк определитель не меняет).

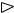Пример 3. Выразить модуль смешанного произведения трех векторов через объем параллелепипеда, построенного на этих векторах (рис. 2).

Решение. Имеем

! !

cos ϕ

Sh = Vпараллелеп ипеда .

(c, a

×b)

×b

Действительно, в силу примера 2

S =

, а h =

cosϕ .

×b

Итак, модуль смешанного произведения равен объему параллелепипеда, построенного на этих векторах. В этом геометрический смысл смешанного произведения.

Пример 4. Найти смешанное произведение векторов:

!	=	!	=	!	= col( 7;8;9) .
a		col (1;2;3), b		col( 4;5;6) , c

7 2

Рис. 2
!	!	!	1	2	3	=
!	!	!	1	2	3
Решение. По формуле (3) получаем (c, a		b) =	4	5	6
			7	8	9
= 1 5 9 + 4 8 3 + 2 6 7 − 7 5 3 − 2 4 9 − 6 8 1			=
= 45 + 96 + 84 − 105 − 72 − 48 = 225 −	225 = 0 ,

т.е. данные векторы компланарны.

! Задания для самостоятельной работы

1. Найти векторное произведение двух векторов:

− 1

−

− 1

а)

; б)

−

; в)

−

2. Найти смешанное произведение трех векторов:

− 1

а)

−

; в)

−

2 ; б)

2 .

−

3. Вычислить площадь параллелограмма, построенного на век-

торах

a =

3 j − 2k

и b

3i −

2 j

6k .

4. Показать, что векторы

! !

2i +

5 j

7k, b =

i +

j −

k , c

= i + 2 j

+ 2k

i +

2 j

+ 2k

компланарны.

5. Найти объем треугольной пирамиды с вершинами А (2; 2; 2), B (4; 3; 3), C (4; 5; 4), D (5; 5; 6).

7 3

Лекция 13

Простейшие задачи аналитической геометрии в пространстве. Плоскость в пространстве

Рассмотрены простейшие задачи аналитической геометрии в пространстве, изучены различные формы уравнения плоскости в пространстве.

10. Простейшие задачи аналитической геометрии в пространстве. Напомним, что декартову систему координат Oxyz в пространстве образуют три взаимно перпендикулярные оси Oz, Oy, Ox, имеющие общее начало и одинаковую единицу масштаба. Точка М пространства, имеющая координаты х (абсциссу), y (ординату) и z (аппликату), обозначается М (x; y; z).

По аналогии с Л.2 расстояние между двумя точками A (x1; y1; z1) и B (x2; y2; z2) определяется по формуле:

d =

− x )2 + (

−

2 +( z

−

z) 2 .

(1)

Если отрезок, концами которого

служат

точки

A (x1; y1; z1) и

B (x2; y2; z2), разделен точкой М (x; y; z)

в отношении λ

, то координаты

точки М определяются по формулам:

x =

x1 +

y =

y1 +

λ y2

, z =

z1 +

λ z2

(2)

Пример 1. Дан треугольник A (1; 1;1),

B (5; 1; –2),

C (7; 9; 1). Найти

координаты точки D

пересечения биссектрисы угла А со стороной СВ.

Решение. По формуле (1) найдем длины стороны треугольни-

ка, образующих угол

А:

(7 − 1)2 + ( 9 − 1) 2 + ( 1− )1 2 = 10 ;

(5 − 1)2 + (1− 1) 2 +( − 2 − )1 2 = 5 .

Следовательно, CD : DB = 10 : 5 = 2 , т.к. биссектриса делит сто-

рону СВ на части, пропорциональные прилежащим сторонам. Таким образом, по формуле (2)

7 4

xD =

xC + λ xB

7 + 2 5

yD =

yC + λ yB

9 + 2 1

1+ λ

1+ 2

1+ λ

1+ 2

zC + λ zB

1+ 2 (− 2)

= − 1 .

Итак, искомая точка

;

− 1 .

20. Общее уравнение плоскости. Пусть плоскость задана

тремя точками A (x1; y1; z1), B (x2; y2; z2) и C (x3; y3; z3). Найдем условие принадлежности произвольной точки М (x; y; z) этой плоскости (рис. 1).

Используем свойство a1) Л.12 смешанного произведения для компланарных векторов:

	AM (AB ×AC )= 0 .				(3)
AM	= col (x −	x1; y −	y1;z − z1) ,
Так как AB =	col (x2 −	x1; y2 −	y1;z2 −	z1) ,
AC =	col (x3 −	x1; y3 −	y1;z3 −	z1) ,
то из (3) получаем	x − x1	y − y1	z − z1	= 0 или
	x − x1	y − y1	z − z1
	x2 − x1	y2 − y1	z2 − z1
	x3 − x1	y3 − y1	z3 − z1
A (x – x1) + B (y – y1) + C (z – z1) = 0,					(4)

Рис. 1

7 5

где A =

y2 − y1

z2 −

, B

z2 −

x2 −

C =

x2 −

y2 −

− y

− z

− x

− y

Обозначая D = – Ax1 – By1 – Cz1

из (4), получаем общее уравнение

плоскости:

Ax + By + Cz + D = 0.

(5)

30. Другие формы

уравнения

плоскости.

а) Уравнение плоскости,

проходящей через точку М (x0; y0; z0)

и перпендикулярной к вектору

col(A; B;C) :

A (x – x0) + B (y – y0) + C (z – z0) = 0.

(6)

col(A; B; C)

называют нормальным вектором плоскости. Из (6)

Вектор n =

видно, что вместо n!

можно взять любой ему коллинеарный вектор.

б) Уравнение плоскости в отрезках на осях:

1 ,

(7)

где a, b, с – длины отрезков, отсекаемых на координатных осях, взятые с соответствующими знаками.

в) Нормальное уравнение плоскости:

x cos α + y cos β + z cos γ– p = 0,

(8)

где cos α , cos β , cos γ – направляющие косинусы нормального вектора, проведенного из начала координат к данной плоскости, а р – его длина.

Для приведения общего уравнения плоскости (5) к нормальному виду (8) следует умножить (5) на нормирующий множитель

v =	1	, где знак перед радикалом противоположен зна-
	A2 + B2 + C 2
±

ку свободного члена D в общем уравнении плоскости.

Пример 2. Составить уравнение плоскости, проходящей через

! ! ! !

точку М (2; 3; 5) и перпендикулярной вектору n = 4i + 3 j + 2k .

Решение. Используем уравнение (6) плоскости, проходящей через данную точку и перпендикулярной данному вектору:

4 (x – 2) + 3 (y – 3) + 2 (z – 5) = 0, т.e. 4x + 3y + 2z – 27 = 0.

Пример 3. Найти уравнение плоскости, проходящей через точку М (2; 3; –1) параллельной плоскости 5x – 3y + 2z – 10 = 0.

7 6

Решение. Запишем уравнение (6) связки плоскостей, проходящих через данную точку:

A (x – 2) + B (y – 3) + C (z + 1) = 0.

Нормальный вектор искомой плоскости совпадает с нормальным

! = ( − )

вектором n col 5; 3;2 данной плоскости. Значит, A = 5, B = –3, C = 2, и уравнение искомой плоскости имеет вид

5 (x – 2) – 3 (y – 3) + 2 (z + 1) = 0 или 5x – 3y + 2z + 1 = 0.

40. Угол ϕ между плоскостями. Угол ϕ между плоскостя-

ми A1x + B1y + C1 z + D1 = 0 и A2x + B2y + C2z + D2 = 0 определяется по формуле:

cos ϕ =

A1 A2 + B1B2 + C1C2

(9)

+ C 2

A2 +

B2 +

C 2

Условие параллельности плоскостей:

(10)

Условие перпендикулярности плоскостей:

A1A2 + B1B2 + C1C2 = 0.

(11)

Пример 4. Составить уравнение плоскости, проходящей

через точки М1 (2; 1; 3), М2 (6; 2; 1)

и перпендикулярной к плоско-

сти 4x + 2y – z + 4 = 0.

Решение. Уравнение плоскости, проходящей через точку

М (2; 1; 3), можно записать в виде (6):

A (x – 2) + B (y – 1) + C (z – 3) = 0.

(12)

Так как плоскость проходит и через точку М2 (6; 2; 1), то ее координаты удовлетворяют уравнению (12), т.е. 4A + B – 2C = 0.

Искомая плоскость перпендикулярна к данной плоскости, поэтому на основании условия (11) 4A + 2B – C = 0. Итак, для определения коэффициентов А, В, С получена система уравнений

4A +		B − 2C =	0,
	4A +	2B − C =	0,

7 7

решение которой имеет вид B = − C, A = 34 C . Подставляя его в уравне-

ние (12), получим нужное уравнение плоскости

3x – 4y + 4z – 14 = 0.

50. Расстояние от точки до плоскости. Расстояние от точки М0 (x0; y0; z0) до плоскости Ax + By + Cz + D = 0 находится по формуле

d =	Ax 0 + By 0 + Cz 0 +	D	(13)
	A2 + B 2 + C 2	.

Пример 5. Определить расстояние от точки M0 (1; 3; –5) до плос-
кости 2x – 3y + 5z – 24 = 0.
Решение. Используя формулу (13), находим:
d = 2 1+ (− 3) 3 + 5 ( − 5) =		32 .
	22 + 32 + 52	38

! Задания для самостоятельной работы

1. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + y + 5z – 1 = 0, 2x + 3y – z + 2 = 0 и через точку

М (3; 2; 1).

2. Составить уравнение плоскости, проходящей через точку М (2; 3; 4) и перпендикулярной к оси Ox.

3.Написать уравнение плоскости, проходящей через ось Oy и

точку М (1; 2; 3).

4.Найти расстояние между параллельными плоскостями:

x – 3y + 6z – 12 = 0 и 2x – 6y + 12z + 36 =0.

5.Найти угол между двумя плоскостями:

а) 4x – 5y + 3z – 1 = 0, x – 4y – z + 9 = 0;

б) x – 3y + z + 5 = 0, 5x – 3y + z – 1 = 0.

6. Найти угол между плоскостями, проходящими через точку М (1; 3; 4), одна из которых содержит ось Oy , другая – ось Oz .

7. Две грани куба лежат соответственно на плоскостях 3x – 2y + 6z – 7 = 0, 3x – 2y + 6z – 35 = 0. Вычислить объем этого куба.

7 8

Лекция 14

Прямая в пространстве

Рассмотрены различные формы уравнения прямой, расположение двух прямых в пространстве.

10. Общее уравнение прямой в пространстве. Прямая может быть задана пересечением двух плоскостей:

A1x +		B1 y + C1z + D1 = 0,		(1)
	A2 x +	B2 y + C2 z + D2 =	0.

Исследуем систему уравнений (1). Пусть

A =

B =

− D1

−

B2 C2

col (A1; B1;C1) =

λ col( A2

;B2 ;C2) =

1. Если n1

λ n2 , т.е. нормальные

векторы к плоскостям коллинеарны, то

−

0 0 0

− D1

+ λ D2

В случае

D1 ≠ λ

имеем

= 1 ≠ rB =2, и система (1) несовме-

стна, т.е. плоскости не пересекаются; если

D1 = λ D2 ,

то плоскости

совпадают.

2. Если

≠

λ n2

, т.е.

нормальные векторы к плоскостям некол-

линеарны,

то

= rB = r = 2,

система

(1)

совместна;

n – r = 3 – 2 = 1,

и плоскости пересекаются, т.е. система уравнений (1)

определяет некоторую прямую. Исключив поочередно х и y из систе-

мы уравнений (1) (если это		возможно),	получим	уравнение
x = k1 z + l1,	y = k2 z + l2. Здесь прямая определена двумя плоскостями,
проектирующими ее на плоскости		Oxz и Oyz .
20.	Параметрическое	и каноническое		уравнение
прямой.	Пусть прямая задана	!	col (l; m;n) и точкой
		вектором a =

M0 (x0; y0; z0). Найдем условие принадлежности точки M (x; y; z) за-
данной прямой (рис. 1). Имеем	*	!	−	!	=	λ	!	, или в координат-
	M 0 M =	r		r0			a

ной форме:

7 9

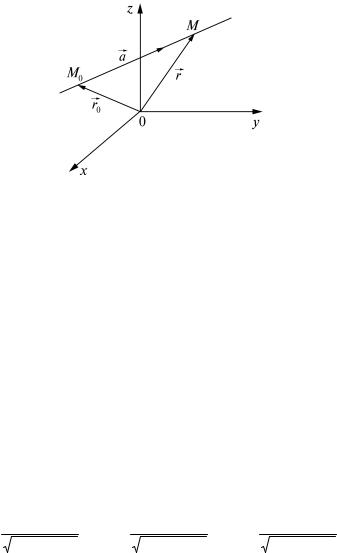
Рис. 1

	x −	x 0	=	λ l,
	y −	y0	=	λ m,	(2)

		z0	=	λ n.
z −

Здесь λ –параметр и соотношения (2) задают параметрическое уравнение прямой.

Параметрическое уравнение прямой (2) можно преобразовать к виду:

x − x0	=	y − y0	=	z − z0	,
l		m		n

которое называется каноническим уравнением прямой.

В частности, уравнения (3) могут быть записаны в виде:

x − x0	=	y − y0	=	z − z0	,
cosα		cosβ		cos γ

(3)

(4)

где α , β , γ– углы, образованные прямой с осями координат. Направляющие косинусы прямой находятся по формулам:

cos α =	l	, cosβ =	m	, cos γ=		n	.
	l 2 + m2 + n2		l 2 + m2 + n2		l 2 +	m2 +
							n2

Из уравнения (3) получаем уравнение прямой, проходящей через две точки M1 (x1; y1; z1) и M2 (x2; y2; z2):

x − x1

y − y1

z − z1

(3′)

− x

− y

− z

8 0

<<< < Предыдущая 1 2 3 4 5 6 78 / 418 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.11.2018253.44 Кб9второй курсач(разработка)(Кристина)2.doc
#
13.09.201940.04 Кб6Вуліца Замкавая.docx
#
18.02.2016147.97 Кб2вучэбная праграма 2012.doc
#
19.02.201612.77 Mб65Высшая матем. Учебник.pdf
#
22.09.2019956.93 Кб18Высшая математика (1).doc
#
18.02.20165.88 Mб72высшая математика.pdf
#
18.02.2016192.33 Кб16Вычеты аналитических функций..pdf
#
18.02.2016190.98 Кб4гістарычная навука Бел. раб. праграма 2012.doc
#
14.04.2019380.93 Кб13Гісторыя Беларус(шпоры).doc
#
12.11.2019311.93 Кб3Гісторыя беларускага сялянства. Т.2..docx
#
15.04.2019130.2 Кб4гістрыя вся.docx