высшая математика

наибольшее из них. Оно и будет наибольшим значением функции f на отрезке [a; b].

Аналогично находится наименьшее значение функции f на отрезке [a; b].

Если функция f дифференцируема на (а; b), то можно поступить следующим образом: найти все стационарные точки функции f на (а; b), вычислить значения функции в стационарных точках и значения f (a) и f (b), тогда наименьшее из них будет наименьшим значением функции на отрезке [a; b], наибольшее из них – наибольшим значением функции.

Задача об отыскании наибольшего и наименьшего значения функции часто возникает в приложениях, в том числе в экономике.

!Задания для самостоятельной работы

1.Определить промежутки монотонности следующих функций:

5. Кусок проволоки длины l согнуть в виде прямоугольника так, чтобы площадь последнего была наибольшей.

2 0 1

Лекция 33

Выпуклость, точки перегиба и асимптоты. Построение графиков функций

Рассматриваются понятия выпуклой функции, точек перегиба и асимптот графика функции. Приводится общая схема построения графиков функции.

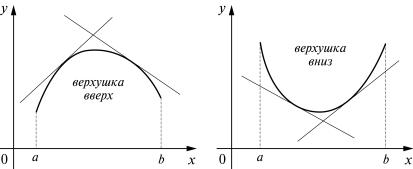
10. Выпуклые функции. Пусть функция f дифференцируема на интервале (а; b). Тогда в каждой точке ее графика существует касательная. Будем говорить, что функция f на интервале (а; b) выпукла вверх, если ее график расположен ниже любой касательной на (а; b); если же график функции расположен выше любой касательной на (а; b), то функция называется выпуклой вниз (рис. 1).

вольную точку x0 (a; b) . Запишем уравнение касательной к графику

Теперь запишем формулу Тейлора для функции f в точке x0 с остаточным членом в форме Лагранжа (см. Л.31, формула (8)), n = 1:

Рис. 1

2 0 2

совпадают, то из сравнения их левых частей следует, что значение у ординаты касательной не больше значения функции в точке х. Значит, график функции f находится выше касательной, и функция f является выпуклой вниз.

Аналогично рассматривается случай, когда f ′′(x ) ≤ 0 .

Говорят, что точка (x0; f (x0)), x0 (a; b) является точкой перегиба непрерывной функции f , если слева и справа от этой точки функция f имеет разные направления выпуклости.

Так, например, точка О (0; 0) является точкой перегиба функции

промежутки выпуклости разной направленности.

Теорема 2 (необходимое условие точки перегиба).

Пусть точка (x0; f (x0)), x0 (a; b) является точкой перегиба

функции f. Тогда, если в точке x0 функция f имеет вторую производную, то f ′′(x 0 ) = 0 .

Таким образом, условие f ′′(x ) = 0 играет такую же роль в отношении точек перегиба, как условие f ′(x ) = 0 в отношении точек локального экстремума. Оно необходимо, но не достаточно. Так, например,

Не будем проводить доказательства теоремы 2. Заметим лишь, что, например, при условии существования непрерывной второй производной в окрестности точки x0 является вполне естественным ее

2 0 3

и построения графиков функций. Для полного исследования поведения функций и построения графиков функций можно рекомендовать следующую схему:

1)найти область определения функции;

2)найти точки разрыва функции, вертикальные асимптоты (если существуют), точки пересечения с осями координат;

3)определить четность (нечетность), периодичность функции;

4)найти промежутки монотонности функции и точки локального экстремума;

5)определить промежутки выпуклости функции и точки перегиба;

6)выяснить вопрос о существовании наклонных асимптот;

7)на основании полученных данных построить график функции (иногда полученные данные сводят в таблицу).

Приведем пример, иллюстрирующий эту схему.

Пример 1. Построить график функции y = e− x 2 .

Решение. 1) Областью определения данной функции является вся числовая прямая.

2) Функция непрерывна на R. Вертикальных асимптот не имеет. График функции ось Ox не пересекает, так как x R : f (x)>0.

Если х=0, то у=1, и ось Oy график функции пересекает в точке (0; 1).

Следовательно, функция является возрастающей на промежутке (–∞ ; 0) и убывающей на (0; +∞ ).

2 0 5

Рис. 2

2 0 6

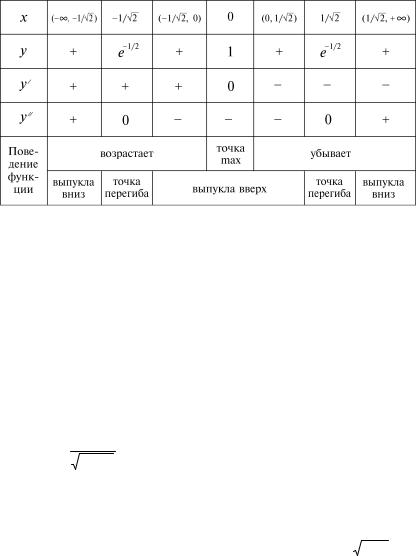
7) Для построения графика полученные результаты сведем в табл. 1.

Таблица 1

На основании полученных данных строим график (рис. 2). Полученная кривая называется кривой Гаусса. Заметим также, что в силу четности функции и симметричности графика относительно оси Oy можно было исследовать функцию лишь на промежутке (0, +∞ ). .

!Задания для самостоятельной работы

1.Определить промежутки выпуклости и точки перегиба следующих функций:

2 0 7

Лекция 34

Первообразная и неопределенный интеграл

Вводятся понятия первообразной и неопределенного интеграла. Изучаются их основные свойства. Приводится таблица основных интегралов.

10. Первообразная. Основной операцией дифференциального исчисления является отыскание производной заданной функции. Однако, естественно, возникает вопрос о существовании операции, обратной дифференцированию. Восстановление функции по известной производной этой функции есть основная задача интегрального исследования.

Функция F называется первообразной для функции f на некото-

Задача об отыскании первообразной по данной функции f реша-

ется неоднозначно. Если, например, F есть первообразная для функции f, то функция F (х) + С также является первообразной для функции f. Действительно, (F ′(x ) + C )′ = F ′(x ) + (C )′ = f (x ) + 0 = f (x ) . В частности, функция (–cos x + C), где С – произвольная постоянной, есть первообразная для функции sin x на R .

Теорема 1.

Если F1 и F2 – две любые первообразные для функции f на промежутке Х, то они могут отличаться лишь на постоянную, т.е. F1(x) –

– F2 (x) ≡ C, С – некоторая постоянная.

Другими словами, если F есть первообразная для функции f, то множество функций F (х) + С описывает все первообразные для данной функции f.

2 0 8

Доказательство теоремы 1. Рассмотрим разность функций F1 и F2. Очевидно,

(F1 (x ) − F2 (x ))′ = F1′(x ) − F2′(x ) = f (x ) − f (x ) = 0 .

Следовательно, по теореме Л.32.1, F1(x) – F2(x) ≡ C, что и требовалось доказать.

Таким образом, если известна хотя бы одна первообразная для дан-

ной функции f, то известно и все множество первообразных для этой функции.

20. Неопределенный интеграл. Множество всех перво-

образных функции f называется неопределенным интегралом функции f и обозначается

∫ f (x ) dx .

Функция f называется подынтегральной функцией, f (x)dx – подынтегральным выражением, переменная х – переменной интегрирования.

Итак, если F есть первообразная функции f на промежутке Х, то

∫ f (x ) dx = F(x ) + C ,

где С – произвольная постоянная.

Подчеркнем, что символ ∫ f (x ) dx обозначает совокупность всех

первообразных для функции f. Но в некоторых случаях он понимается как отдельный элемент из этой совокупности, т.е. определяет какуюлибо одну функцию.

Отыскание неопределенного интеграла по подынтегральной функции называется интегрированием этой функции.

2 0 9

1) Производная неопределенного интеграла равна подынтегральной функции, т.е.

( ∫ f (x )dx)′ = f (x ) .

Действительно, ( ∫ f (x )dx)′ = (F (x ) + C)′ = f (x ) .

2) Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

d∫ f (x )dx = f (x )dx .

Действительно, d ∫ f (x )dx = ( ∫ f (x )dx)′dx = f (x )dx .

3) Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

∫dF(x ) = F(x ) + C .

Действительно, ∫dF(x ) = ∫F ′(x )dx = F(x ) + C .

4) Постоянный множитель можно выносить за знак интеграла,

т.е. если k = const ≠ 0 , то

∫kf (x )dx = k ∫ f (x )dx .

Действительно, пусть F есть первообразная для функции f. Тогда, учитывая, что функция kF будет первообразной для функции kf, имеем:

∫kf (x )dx = kF (x ) + C = k (F(x ) + C1 ) = k ∫ f (x )dx .

5) Неопределенный интеграл от суммы двух функций равен сумме интегралов от этих функций, т.е.

∫( f (x ) + g(x ))dx = ∫ f (x )dx + ∫g(x )dx .

Действительно, пусть F и G – первообразные для функции f и g,

F ′(x ) = f (x ) , G′(x ) = g(x ) .

Тогда функция F + G является первообразной для функции f + g,

(F(x ) + G(x ))′ = F ′(x ) + G′(x ) = f (x ) + g(x ) .

Следовательно,

∫ f (x )dx + ∫g(x )dx = F(x ) + C1 + G(x ) + C2 = = F(x ) + G(x ) + (C1 + C2 ) = ∫( f (x ) + g(x )) dx .

2 1 0