
высшая математика
.pdf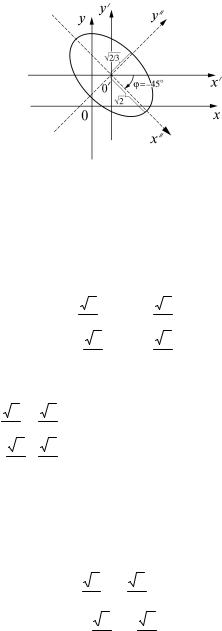
Рис. 4
Решим систему уравнений, чтобы найти собственные векторы:
( − λ ) !i = .
A i E x 0
Получаем ортонормированную систему собственных векторов:
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
! |
|
|
|
|
|
|
! |
|
|
|
|
||
1 |
= |
|
|
2 |
|
, |
2 |
= |
|
2 |
|
||
x |
|
x |
|||||||||||
|
|
|
|
− |
2 |
|
|
|
|
|
|
2 |
. |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем оператор поворота:
|
|
|
2 |
2 |
|
|
|
|
cos(− ϕ ) |
sin( − ϕ) |
|
T = |
|
|
2 |
2 |
|
= |
R (− ϕ ) = |
= |
|||
|
|
|
|
|
|
||||||
|
|
− |
2 |
2 |
|
|
|
|
− sin(− ϕ ) |
|
|
|
|
|
|
|
|
cos( − ϕ) |
|
||||
|
|
|
2 |
2 |
|
|
|
|
|
|
|
= |
|
|
cos 450 |
sin 450 |
|
|
ϕ = − 45 |
0 |
. |
||
|
|
|
0 |
|
0 |
|
|
||||
|
|
− |
sin 45 |
cos 45 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
Преобразование поворота:
|
2 |
x′+ |
2 |
y′, |
||
x′= |
||||||
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
|
x′+ |
|
y′. |
||
y′= − |
2 |
2 |
||||
|
|
|
||||
101

|
2 |
|
2 |
|
|||
Итак, каноническое уравнение заданной кривой |
(x ′) |
+ |
|
(y′) |
= 1 – |
||
2 |
|
2 |
|
||||
|
|
|
|
||||
|
|
|
3 |
|
|
||
эллипс; ϕ = − 450 . Построение кривой изображено на рис. |
4. |
|
|
|
|||
! Задания для самостоятельной работы
1. Найти уравнение окружности, касающейся осей координат и проходящей через точку М (3; 1).
2. Определить полуоси, фокусы и эксцентриситет каждого из следующих эллипсов:
|
a) |
x 2 |
+ |
y 2 |
= 1 ; |
б) 2x |
2 |
+ 4y |
2 |
= 3; в) |
x |
2 |
+ 3y |
2 |
= 36. |
|
8 |
9 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3. Составить уравнение эллипса, длина большей полуоси кото- |
||||||||||||||
рого равна 20, а фокусами служат точки F1 |
(–1; 0) и F2 (5; 0). |
||||||||||||||
|
4. Составить уравнение гиперболы, зная, что расстояние между |
||||||||||||||
ее вершинами равно 24 и фокусы находятся в точках F1 (–10; 2) и |
|||||||||||||||
F2 |
(16; 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Найти координаты фокуса и записать уравнение директрисы |
||||||||||||||
каждой параболы, |
заданной уравнением: |
|
a) y2 = 14x; б) x2 = –8y; |
||||||||||||
в) y2 = –16x.
6. Найти канонические уравнения кривых, угол их поворота и построить кривые:
а) 16x2 – 9y2 – 64x – 54y – 161 = 0; б) 4x2 + 4x + 3y – 2 = 0;
в) 2x2 + xy – y2 + 5x – 7y + 2 = 0; г) 3x2 + 2xy – 5y2 + x – y = 0;
д) 7x2 + xy + 14y2 – x + 2y = 0.
102
 Лекция 18
Лекция 18
Сфера, цилиндрические поверхности и конус второго порядка
Изучаются канонические уравнения сферы, цилиндрических поверхностей и конуса второго порядка.
10. Сфера. Точками сферы являются те и только те точки пространства, расстояние от которых до заданной точки М равно R. В декартовой системе координат сфера, имеющая центр в точке М (а; b; с) и радиус R, определяется уравнением:
(x – a)2 + (y – b)2 + (z – c)2 = R2. |
(1) |
Если центр сферы находится в начале координат, то ее уравнение имеет вид:
x2 + y2 + z2 = R2. |
(1′) |
 Пример 1. Найти координаты центра и радиус сферы, заданной уравнением x2 + y2 + z2 – 2x + 2y + z + 1 = 0.
Пример 1. Найти координаты центра и радиус сферы, заданной уравнением x2 + y2 + z2 – 2x + 2y + z + 1 = 0.
Решение. Приведем уравнение сферы к каноническому виду (1). Для этого дополним до полных квадратов члены, содержащие x, y, z, т.е. перепишем уравнение в виде:
|
(x |
2 |
|
1)+ (y |
2 |
|
|
|
1) + |
|
2 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|||
|
|
− 2x + |
|
+ 2y + |
z |
|
+ |
z + |
|
|
|
|
− 1 |
− 1 |
− |
|
|
+ |
1 = 0 |
||||||||
|
|
|
|
|
|
|
4 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
или (x − 1) |
2 |
|
( y + |
1) |
2 |
|
|
|
1 |
|
5 |
. |
|
|
|
|
|||||||
|
|
|
|
|
+ |
|
+ |
z |
+ |
|
|
|
|
= |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
4 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
Следовательно, центр сферы – точка |
M |
1; − |
|
1; − |
|
|
, а ее радиус |
|||||||||||||||||||
|
|
|
2 |
||||||||||||||||||||||||
R = |
5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. |
Составить уравнение сферы, |
проходящей через точ- |
||||||||||||||||||||||||
ки А (1; 2; –4), В (1; –3; 1) и С (2; 2; 3), если ее центр находится в плоско-
сти Oxy.
Решение. Так как точки А, В и С принадлежат сфере (x – a)2 + (y – b)2 + (z – c)2 = R2, центр которой находится в плоскости Oxy,
то их координаты должны обращать искомое уравнение в тождество и c = 0. Поэтому имеем систему уравнений:
103

|
(1− a)2 + ( 2 − b) 2 +( − 4) 2 = R2 , |
|
|
|
|
||
|
(1− a)2 + ( − 3 − b) 2 + 12 = R2 , |
|
|
|
|
||
|
(2 − a)2 + ( 2 − b) 2 + 32 = R2 . |
|
|
|
|
||
(1− |
|
2 + 16 = ( 1− a) |
2 +( − 3 − )b |
|
|
|
|
a)2 + ( 2 − b) |
2 + 1, |
|
|
||||
Отсюда |
a)2 + ( 2 − b) |
2 + 16 = ( 2 − a) |
2 +( 2 − )b 2 |
+ 9. |
|
||
(1− |
|
|
|||||
|
|
|
|
|
|
|
|
|
(2 − b)2 − ( − |
3 − b) 2 = − 15 10b = 10, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
− a) 2 = − 7 2a = − 4. |
|
|
|
|
|
(1− a)2 − ( 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
Таким образом a = –2, b = 1. Следовательно, |
центр сферы – |
точ- |
|||||
ка М (–2; 1; 0). |
Дальше |
находим |
R2 = (1 – a)2 + (2 –b)2 + 16 = |
||||
= 32 + 12 + 16 = 26. |
Итак, искомое уравнение имеет вид (x + 2)2 + (y – |
||||||
– 1)2 + z2 = 26. |
|
|
|
|
|
|
|
20. Цилиндрические |
поверхности. |
Уравнение |
вида |
||||
F (x, y) = 0 в пространстве определяет цилиндрическую поверхность, у которой образующие параллельны оси Oz. Аналогично, уравнение F (x, z) = 0 определяет цилиндрическую поверхность с образующими
параллельными оси Oy, а F (y, z) = 0 |
|
– цилиндрическую поверхность с |
||||||
образующими параллельными оси Ox. |
|
|||||||
Канонические уравнения цилиндров второго порядка: |
|
|||||||
эллиптический цилиндр |
x2 |
+ |
|
y2 |
|
= |
1 , |
(2) |
a2 |
|
b2 |
||||||
|
|
|
|
|
|
|||
гиперболический цилиндр |
x2 |
− |
|
y2 |
|
= |
1 , |
(3) |
a2 |
|
b2 |
||||||
|
|
|
|
|
|
|||
параболический цилиндр |
y2 = |
2 px . |
(4) |
|||||
Образующие всех трех цилиндров, определяемых уравнениями (2), (3), (4), параллельны оси Oz, а направляющей служит соответствующая кривая второго порядка (эллипс, гипербола, парабола), лежащая в плоскости Oxy.
Следует знать, что кривую в пространстве можно задать либо параметрически, либо в виде линии пересечения двух поверхностей. Например, уравнения направляющей эллиптического цилиндра, т.е. уравнения эллипса в плоскости Oxy, имеют вид
x2 |
+ |
y2 |
= |
1, z = |
0 . |
|
a2 |
b2 |
|||||
|
|
|
|
104

Рис. 1
 Пример 3. Определить, какую поверхность в пространстве задает уравнение x2 = 5y .
Пример 3. Определить, какую поверхность в пространстве задает уравнение x2 = 5y .
Решение. Уравнение x2 = 5y определяет параболический цилиндр с образующими параллельными оси Oz. Направляющей цилиндрической поверхности является парабола x2 = 4y, z = 0. 
Замечание 1. В Л.3 введена полярная система координат на плоскости.
В трехмерном пространстве полярная система координат называется цилиндрической, при этом так же, как и декартова, она дополняется координатой z (рис. 1).
Связь декартовой системы координат с цилиндрической следующая:
x = |
ρ |
cos ϕ , |
ρ |
= |
|
x 2 + |
y 2 , |
|
|
|
|
|
|
|
|
y |
|
y = |
ρ |
sin ϕ , |
ϕ |
= |
arctg |
|
, |
|
|
||||||||
z = |
z ; |
z = |
z. |
|
x |
|||
|
|
|
||||||
30. Конус второго порядка. Уравнение конуса второго порядка с вершиной в начале координат, осью которого служит ось
Oz, записывается в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x2 |
+ |
|
y2 |
− |
|
z2 |
= |
0 . |
|
|
|
|
|
|
|
|
(5) |
||||
|
a2 |
|
b2 |
|
c2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Геометрически коническую поверхность можно изобразить, как |
||||||||||||||||||||||
показано на рис. 2. |
|
x2 |
|
|
y2 |
|
|
z2 |
|
|
|
x2 |
|
y2 |
|
z2 |
|
|
||||
Аналогично, уравнения |
− |
+ |
= |
0, − |
+ |
+ |
= |
0 явля- |
||||||||||||||
a2 |
b2 |
c2 |
a2 |
b2 |
c2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ются уравнениями конусов второго порядка с вершиной в начале координат, осями которых служат соответственно оси Oy, Ox.
 Пример 4. По какой линии пересекается конус x2 + y2 – 2z2 = 0 с плоскостью у = 2 ?
Пример 4. По какой линии пересекается конус x2 + y2 – 2z2 = 0 с плоскостью у = 2 ?
105
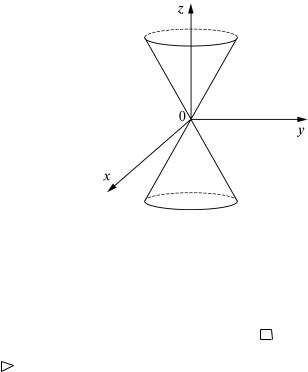
|
|
|
|
|
|
|
|
Рис. 2 |
|
Решение. Исключив |
|
из системы уравнений у, получим |
|||||
x2 |
+ 4 – 2z2 |
= 0 или |
z 2 |
− |
x 2 |
= |
1 . Значит, искомой линией пересечения |
|
2 |
4 |
|
||||||
|
|
|
|
|
|
|
||
будет гипербола, лежащая в плоскости y = 2; ее действительная ось параллельна оси Oz, а мнимая – оси Ox.
Пример 5. Составить уравнение конической поверхности, вершиной которой служит точка М (1; 1; 1), а направляющей – эллипс
(x − 1)2 |
+ |
(y − 1)2 |
= |
1, z = |
3. |
|
25 |
9 |
|||||
|
|
|
|
Решение. Составим уравнение образующей АМ, где A (x0; y0; z0) – точка, лежащая на эллипсе. Это уравнение имеет вид
|
x − 1 |
|
= |
y − 1 |
|
= |
|
z − |
1 |
. Так как точка А лежит на эллипсе, |
то ее коор- |
|||||||||||||||||||
|
x0 − 1 |
|
y0 − 1 |
|
z0 − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
динаты удовлетворяют уравнению эллипса, т.е. |
x2 |
|
|
y2 |
1, z0 = 3 . |
|||||||||||||||||||||||||
|
0 |
+ |
|
0 |
= |
|||||||||||||||||||||||||
25 |
9 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Исключив |
|
|
x0, y0, z0 |
из системы |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x − 1 |
= |
z − 1 |
|
, |
y − 1 |
|
= |
z − 1 |
, |
(x0 − 1)2 |
+ |
(y0 − 1)2 |
|
= |
|
1, z0 = 3, |
||||||||||||
|
|
|
z0 − 1 |
y0 − 1 |
|
25 |
9 |
|
|
|
||||||||||||||||||||
|
|
x0 − 1 |
|
|
z0 − 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
получим уравнение искомого конуса:
106

|
(x − 1)2 |
+ |
(y − |
1)2 |
− |
|
|
(z − 1)2 |
= |
0 . |
||||
25 |
9 |
|
|
|
9 |
|||||||||
|
|
|
|
|
|
|
||||||||
40. Пары плоскостей. Пара пересекающихся плоскостей за- |
||||||||||||||
дается уравнением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
− |
|
|
y2 |
|
= 0 ; |
|
(6) |
||
|
|
|
|
a2 |
|
|
b2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
пара параллельных плоскостей |
|
|
|
задается уравнением |
||||||||||
|
|
|
|
|
x |
2 |
= |
1 , |
|
(7) |
||||
|
|
|
|
|
a2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
а пара совпадающих плоскостей |
|
|
|
|
|
|||||||||
|
|
|
|
|
x2 = 0. |
|
(8) |
|||||||
Пример 6. Какую поверхность определяет в пространстве урав- |
||||||||||||||
нение z2 = xz ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Уравнение z2 = xz |
|
|
может быть представлено в виде |
|||||||||||
z(z − x) = 0 и распадается на два уравнения |
z = 0, z = x, т.е. оно опре- |
|||||||||||||
деляет две пересекающиеся плоскости – плоскость Oxy и биссектральную плоскость z = x, проходящую через ось Oy. 
! Задания для самостоятельной работы
1. Найти координаты центра и радиус окружности:
|
3) |
2 |
+ |
( y + 2) |
2 |
+( z − )1 |
2 |
= 100, |
(x − |
|
|
|
|||||
|
2y − z + 9 = |
|
0. |
|
|
|||
2x − |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2.Составить уравнение плоскости, проходящей через центр сферы x2 + y2 + z2 + 2x – y + 5z = 0 и перпендикулярной прямой, проходящей через точки М1 (2; 5; –1) и M2 (4; 6; 0).
3.Установить, какие поверхности в пространстве определяются следующими уравнениями, и построить эти поверхности:
a) x2 + y2 = 4; б) x2 – y2 = 1; в) y2 = 2x; г) z2 = 5y; д) x2 + y2 = 3y; е) x2 + 2y2 = 0.
4. Составить уравнение линий пересечения конуса x2 – y2 + z2 = 0 с плоскостями а) y = 3; б) z = 1.
5. Составить уравнение конуса с вершиной в начале координат, направляющая которого задана уравнением x = a, y2 + z2 = b2.
107

 Лекция 19
Лекция 19
Поверхности вращения. Общее уравнение поверхности второго порядка
Рассматриваются поверхности вращения, канонические формы однополостного и двуполостного гиперболоидов и эллиптического параболоида, изучается общее уравнение поверхности второго порядка.
10. Поверхности вращения. Если лежащая в плоскости Oyz кривая F (y, z) = 0, x = 0 вращается вокруг оси Oz, то уравнение образуемой ею поверхности вращения имеет вид
|
± |
x |
2 |
+ y |
2 |
|
|
= 0 , |
|
|
|
|
F |
|
|
, z |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично, уравнение |
|
|
|
± |
y |
2 |
+ z |
2 |
= 0 |
определяет поверх- |
||
F x, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ность, образованную вращением вокруг оси Ox кривой F (x, y) = 0,
z = 0; уравнение |
|
± |
x |
2 |
+ |
z |
2 |
|
= 0 |
– поверхность, образованную |
F |
|
|
, y |
|||||||
|
|
|
|
|
|
|
|
|
|
|
вращением этой же кривой вокруг оси Oy.
Приведем уравнение поверхностей вращения, образованных вращением эллипса, гиперболы и параболы вокруг их осей симметрии.
а) Эллипсоид вращения
Рис. 1
108
|
x2 + y2 |
+ |
z2 |
= |
1. |
(1) |
|
a2 |
c2 |
||||
|
|
|
|
|
||
Здесь осью вращения является ось |
Oz; эллипсоид сжат при |
a > c |
||||
и удлинен при a < c (рис. 1); |
при a = c |
он превращается в сферу. |
|||||
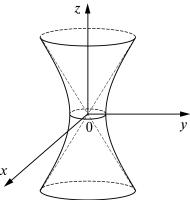
б) Однополостный гиперболоид вращения (рис. 2) |
|||||||
|
x2 + y2 |
|
− |
z |
2 |
= 1 . |
(2) |
|
a2 |
|
c |
2 |
|||
|
|
|
|
|
|||
Осью вращения является ось Oz, служащая мнимой осью гиперболы, вращением которой образована эта поверхность.
в) Двуполостный гиперболоид вращения
x2 + y2 |
− |
z2 |
= − 1 . |
(3) |
|
a2 |
c2 |
||||
|
|
|
Осью вращения является ось Oz, служащая действительной осью гиперболы, вращением которой образована эта поверхность (рис. 3).
г) Параболоид вращения
x2 + y2 = 2 pz |
(4) |
имеет ось вращения Oz.
20. Канонические формы некоторых поверхностей второго порядка. Поверхности вращения второго порядка являются частным случаем поверхностей второго порядка общего вида, канонические уравнения которых следующие:
Рис. 2
109
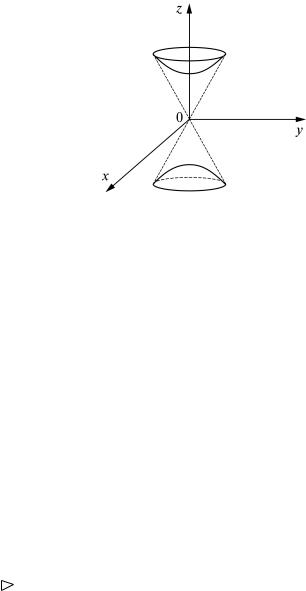
Рис. 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
д) эллипсоид (трехосный) |
x2 |
+ |
|
y2 |
|
|
+ |
|
|
z2 |
|
= 1; |
|
|
|
|
|||||||||
a2 |
|
b2 |
|
|
|
|
c2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
е) однополостный гиперболоид |
|
|
x |
2 |
|
|
+ |
|
|
|
y |
2 |
|
− |
z2 |
= |
1; |
||||||||
|
|
a |
2 |
|
|
|
|
b |
2 |
|
c2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ж) двуполостный гиперболоид |
|
x2 |
+ |
|
|
|
y2 |
− |
|
z |
2 |
|
= − |
1; |
|||||||||||
|
a2 |
|
|
b2 |
|
c |
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
з) эллиптический параболоид |
|
x2 |
|
+ |
|
|
|
y 2 |
|
= |
|
|
2z |
|
(p > |
0, q > 0) . |
|||||||||
|
p |
|
|
|
|
|
q |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(5)
(6)
(7)
(8)
Кроме этих четырех поверхностей второго порядка, трех цилиндров второго порядка и конуса второго порядка, имеется еще одна поверхность второго порядка – гиперболический параболоид, каноническое уравнение которого имеет вид:
и) |
x2 |
− |
y2 |
= 2z (p > 0, q > |
0) . |
(9) |
|
|
|||||
|
p |
q |
|
|
||
Итак, всего существует девять различных поверхностей второго |
||||||
порядка. |
|
|
|
|
|
|
Пример 1. Найти уравнение поверхности, полученной при вра- |
||||||
щении прямой x + 2y = 4, z = 0 вокруг оси |
Ox. |
|
||||
Решение. Пусть A (X; Y; Z) – произвольная точка искомой поверхности. Ей соответствует на данной прямой точка B (x; y; 0).
110
