Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

высшая математика

.pdf

Скачиваний:

Добавлен:

18.02.2016

Размер:

5.88 Mб

Скачать

☆

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 2223 / 4123 24 25 26 27 28 29 30 31 32 33 34 35 > Следующая >>>

(x ) =

A(x − x

)l1 (x −

)l2 ...(x − x

)lr (x 2

+ 2 p x +

q )t1 ×

×(x 2 +

2 p2 x +

q2 )t2 ...(x 2 +

2 ps x +

qs )ts ,

(1)

где x , x

, ..., x

R, l , l

, ..., l

N, t , t , ..., t

N и p 2 – q < 0, i = 1, 2,..., s.

1 2

Последнее означает, что многочлены x2 + 2p x + q

не имеют действитель-

ных корней.

Этот факт устанавливается в расширенном курсе высшей мате-

матики. Также примем без доказательства следующее утверждение:

если QP((xx)) есть правильная рациональная функция и многочлен Q(x)

имеет вид (1), то ее можно единственным образом представить в виде:

P(x )

∑l1

Ak(1)

∑l2

Ak(2)

... + ∑lr

Ak(r)

Q(x )

k = 1 (x − x1 )

k = 1 (x − x2 )

k = 1 (x − xr )

(1)

(2)

( s)

+ ∑

M k x +

N k

+ ∑

M k

x + N k

+ ... + ∑

M k

x + N k

, (2)

1 (x

+ 2 p1x

q1 )

+ 2 p2 x + q2 )

1 (x

+ 2 ps x +

qs )

k =

k = 1

k =

где

Ak(i ) , M k(i )

N k(i )

– некоторые вещественные числа.

Выражение (2) называется разложением на простейшие рациональные дроби. Поскольку в Л.30 мы рассмотрели методы интегрирования таких дробей, то, имея разложение (2), легко найти неопреде-

ленный интеграл от рациональной функции QP((xx)) .

Этот интеграл будет также выражаться через рациональные функции, логарифмы и арктангенсы. Таким образом, главная задача при интегрировании рациональных функций состоит в нахождении раз-

ложения (2). Если известно представление (1), то коэффициенты Ak(i ) ,

M k(i ) , N k(i ) ищутся методом неопределенных коэффициентов. Суть его состоит в следующем. Записывается представление (2) с неопределенными коэффициентами Ak(i ) , M k(i ) , N k(i ) . Затем выражение в правой части приводим к общему знаменателю и получим в числителе некоторый многочлен. Сравнивая коэффициенты при одинаковых степенях у этого многочлена и многочлена P(x), получаем систему уравнений для определения коэффициентов Ak(i ) , M k(i ) , N k(i ) .

Решив ее, найдем эти коэффициенты. Проиллюстрируем изложенное на примерах.

2 2 1

Пример 1. Найти разложение на простейшие дроби рациональной

функции R(x ) =	x
		.
	(x + 1)(x − 2)(x 2 + 1)

Решение. Очевидно, это есть правильная рациональная функция, и ее знаменатель имеет вид (1). Поэтому запишем представление (2) с неопределенными коэффициентами для данной рациональной функции:

x	=	A		+	B	+	Mx + N	.	(3)
(x + 1)(x − 2)(x 2 + 1)		x +	1		x − 2		x 2 + 1

Правую часть равенства (3) приводим к общему знаменателю и сравниваем многочлены, стоящие в числителях левой и правой частей:

x = A(x – 2)(x2 + 1) + B(x + 1)(x2 + 1) + (Mx + N)(x + 1)(x – 2)
или
x = (A + B + M) x3 + (–2A + B + N – M) x2 +
+(A + B –2M – N) x – 2A + B – 2N.	(4)

Два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях х. Приравнивая эти коэффициенты, получим систему уравнений для определения чисел А, В, М, N:

при x3	:	A + B + M = 0;	(5)
при x2 : –2A + B + N – M = 0;
при x1		: A + B – 2M – N = 1;
при x0		: –2A + B – 2N = 0.	(6)

Решая эту систему из четырех линейных уравнений, находим неизвестные А, В, М и N.

Вместе с тем, используя тождество (4), можно найти искомые коэффициенты несколько проще:

а) полагая в (4), х = –1, получаем –1 = A(–3 × 2),

откуда A =

;

б) полагая в (4), х = 2, получим

2 = B × 3 × 5,

откуда

B =

;

в) тогда из уравнения (5) находим M= – A – B = −

−

= – 0,3, а

из уравнения (6) N =

−

A =

−

= –0,1.

Таким образом,

− 0,1

3x +

(x + 1)(x − 2)(x 2 +

6(x +

15(x −

x 2 +

2 2 2

Пример 2. Найти разложение на простейшие дроби для рацио-

2x + 1

нальной функции (x 2 + 5x + 6)(x + 2) .

Решение. Данная рациональная функция является правильной. Нетрудно видеть, что корнями многочлена x2 + 5x + 6 являются числа

(–2) и (–3). Поэтому (x2 + 5x + 6)(x + 2) = (x + 2)2 (x + 3).

Поэтому можем записать следующее представление с неопределенными коэффициентами, аналогичное формуле (2):

x	=	A	+	B	+	C	.
(x + 2)2 (x + 3)		x + 2		(x + 2)2		x + 3

Приводя выражение справа к общему знаменателю и сравнивая многочлены, стоящие в числителе, находим:

x = A(x + 2)(x + 3) + B(x + 3) + C(x + 2)2.

Полагая здесь х = –2, находим –2 = В(–1) и В = –2.

Если положить х = –3, то имеем –3 = C(–1)2 и C = –3.

Наконец,

если

х = 0,

то

получим

6A + 3B + 4C = 0 и

A = −

(3B + 4C) = 3 .

Значит,

−

(x 2 +

x +

(x +

2)2

x + 3

5x + 6)(x + 2)

20. Интегрирование иррациональных функций. Через

R(u, v) будем обозначать рациональную функцию двух переменных, т.е.

функцию, получающуюся из двух переменых u и v и некоторых постоянных, над которыми производятся операции сложения, вычитания, умножения и деления. Например, функция

u2v2 + 3u2v+ uv2 + uv+ 1

u2v+ u2 + 2

есть рациональная функция двух переменных u и v. Пусть имеем интеграл вида

		n ax +
	x,	n ax +	b	dx ,	(7)
∫R	x,			dx ,	(7)
		cx +	d

где n N , ad – bc ≠ 0.

2 2 3

В интегралах такого вида целесообразно сделать следующую замену:

n ax +

t .

(8)

cx +

Из этого равенства получим:

t n =

ax + b

b − dt n

dx =

m(ad − bc)t n− 1

dt .

cx + d

ct n − a

(ct n − a)2

Подставляя соответствующие выражения в (7), получим:

x, n

ax +

b − dt n

m(ad − bc)t n− 1

dt =

(t) dt

∫

dx =

∫

, t

∫

cx +

− a

(ct

− a)

где R1(t) есть некоторая рациональная функция переменной t. Таким образом, интегралы вида (7) заменой переменной (8) сводятся к интегралам от рациональных функций, методы вычислений которых нам уже известны. В этом случае говорят, что интеграл вида (7) рационализируется.

Пример 3.

Найти интеграл

∫

x − 1 dx .

x + 1

Решение.

Сделаем замену

переменной

x + 1 = t . Имеем

x + 1 = t2 , x = t2 – 1 , dx = 2t dt и

∫

x − 1

dx =

∫

t 2

−

1− 1

2t dt =

∫

− 2) dt =

t 3

−

2t + C =

x + 1

( x

+ 1)3

−

x + 1(x − 5)

+ C .

= 2

2 x + 1 + C

30. Тригонометрические интегралы. Пусть имеем ин-

теграл вида

∫R(sin x, cos x ) dx ,

(9)

где R(u, v) – рациональная функция двух переменных u и v.

В этом случае функцию R (sin x, cos x) называют тригонометрической рациональной функцией.

Интеграл (9) рационализируется (т.е. приводится к интегралу от алгебраической рациональной функции) с помощью замены переменной

2 2 4

= tg

Действительно,

2 tg

1−

1− t 2

sin x =

cos x =

2 x

t 2

1+ tg

x =

2 arctg t ,

dx =

2dt

t 2

∫

1− t 2

∫

R(sin x, cos x )dx

dt =

(t)dt ,

+ t

+ t 1

где R1(t) – рациональная функция переменной t.

(10)

(11)

Пример 4. Вычислить интеграл ∫

2 +

cos x

Решение.

Положим

t =

. Тогда, воспользовавшись фор-

мулами (11),

имеем

∫

= 2∫

2∫

+ cos x

1− t

2(1+

) + 1−

1+ t

2 arctg tg

arctg

+ C =

+ C .

На практике замена переменной (10) приводит часто к громоздким выкладкам. При определенных условиях более удобны другие замены переменной:

а)	если R(–sin x, cos x) = –R(sin x, cos x),	то полагают t = cos x;
б)	если R(sin x, –cos x) = –R(sin x, cos x),	то полагают t = sin x;
в)	если R(–sin x, –cos x) = –R(sin x, cos x), то полагают t = tg x.

2 2 5

!Задания для самостоятельной работы

1.Найти следующие интегралы:

а) ∫

2x +

; б) ∫

x 3 +

dx ; в) ∫

x 2

dx ;

x 2 + 3x − 10

x 3 − 5x 2 + 6x

(x 2 − 3x + 2)2

г) ∫

; д) ∫

−

4x +

4)(x

− 4x +

Найти следующие интегралы:

а) ∫x

x + 1dx ; б)

∫

1− x −

(1− x )3

; в) ∫3 x + 1dx ;

x − 1

1− x

г) ∫

x + 1 −

x − 1 dx ; д) ∫

x + 1 +

x − 1

x(1+ 2 x +

x )

Найти следующие интегралы:

а)

∫

; б)

∫

sin x

;

в) ∫

tg x

;

+ 2 cos x

1− sin x

1−

tg x

г)

∫

sin 2x

dx ; д)

∫sin

x cos

x dx

;

е)

∫sin

x cos

x dx .

+ sin

2 2 6

Лекция 37

Определенный иинтеграл

Вводится понятие определенного интеграла. Рассматривается его геометрический смысл. Изучаются основные свойства определенного интеграла, оценки интегралов и теорема о среднем значении определенного интеграла.

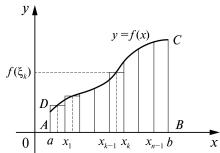
10. Задача о вычислении площади криволинейной трапеции. Пусть на отрезке [a; b] задана непрерывная неотрицательная функция у = f (x) (рис. 1). Рассмотрим фигуру ABCD, ограниченную графиком функции у = f (x), прямыми х = а, х = b и осью Ox. Ее называют криволинейной трапецией. Поставим задачу об определении и вычислении площади этой криволинейной трапеции. С этой целью отрезок [a; b] разо-

бьем на n произвольных частей точками:
a = x0 < x1 < x2 < ... < xk — 1 < xk < ... < xn = b.
Через точки xk , k = 0, 1,	..., n проведем прямые, параллельные оси
Oy. Криволинейная трапеция АВСD разобьется на n частичных криво-
линейных трапеций. Теперь на каждом из отрезков [x0; x1], [x1; x2],		...,
[xn–1; xn] произвольно выберем по точке ξ k, ξ k [xk-1 ; xk] , k = 1, 2, ...,		n,
вычислим значение f (ξ k), k = 1, 2, ..., n. И каждую частичную криволи-
нейную трапецию заменим прямоугольниками с высотами f (ξ 1), f (ξ		2),
..., f (ξ n). Тогда можно полагать, что для площади S криволинейной
трапеции АВСD справедливо соотношение
S ≈ ∑n	f (ξ k )(x k − x k − 1 ) .
k = 1

Рис. 1

2 2 7

Естественно предположить, что это равенство будет тем точнее, чем

меньше max (x k − x k − 1 ) =	λ . Поэтому площадь криволинейной трапеции
1≤ k ≤ n
S определяют как
lim ∑n		f (ξ k )(x k − x k − 1 ) .	(1)
λ →	0 k = 1

Число S, равное пределу (1), называют определенным интегра-

лом от функции f по отрезку [a; b] и обозначают ∫ f (x ) dx . Таким

образом, задача о вычислении площади криволинейной трапеции приводит к введению понятия определенного интеграла.

20. Определение определенного интеграла. Пусть функция f определена на отрезке [a; b]. Разобьем этот отрезок на n частей точками xk, k = 0,1,...,n:

a = x0 < x1 < x2 < ... < xk-1 < xk < ... < xn = b.

Введем следующие обозначения:

∆xk = xk – xk–1	, k = 1, 2, ..., n, λ = max ∆x k .
	1≤ k ≤ n

В каждом из по точке ξ k, ξ k сумму:

частичных отрезков [xk–1; xk] произвольно выберем [xk–1; xk], k = 1, 2, ..., n. Рассмотрим следующую

σ = ∑n

f (ξ k )∆x k .

(2)

k = 1

Сумма (2) называется интегральной суммой для функции f на

отрезке [a; b].

Число А называется пределом интегральных сумм (2) при λ →

если ε > 0 δ = δ(ε) > 0

такое, что для любого разбиения отрезка

[a; b] точками

, k = 0,

1, ...,

n, для которого λ < δ, при любом выбо-

ре точек ξ

; x ] выполняется неравенство:

k–1 k

σ − A

∑n

f (ξ k )∆x k − A

< ε .

k = 1

Другими словами, предел интегральных сумм не должен зави-

сеть ни от способа разбиения отрезка [a; b], ни от выбора точек ξ k на

отрезках [xk–1; xk].

Функция f называется интегрируемой на отрезке [a; b], если существует конечный предел А ее интегральных сумм (2) на этом отрезке. Число А называется определенным интегралом функции f на отрезке [a; b] и обозначается:

2 2 8

b
∫ f (x )dx .	(3)

Числа а и b называются нижним и верхним пределами интегрирова-

ния.

На основании предыдущего пункта заключаем, что геометрический смысл определенного интеграла (3) состоит в том, что он равен площади криволинейной трапеции, если f (x) ≥ 0 (рис. 1).

Из определения интеграла следует, что значение интеграла (3) есть число, зависящее от вида функции f, пределов интегрирования а и b и не зависящее от выбора обозначения переменной интегрирования.

Позже мы установим связи между определенным и неопределенным интегралами функции f.

Пример 1. Найти определенный интеграл ∫1 dx .

Решение. Построим для функции f (x) = 1 на отрезке [a; b] интегральную сумму

σ = ∑n	f (ξ k )∆x k = ∑n ∆x k .
k = 1	k = 1
Учитывая, что ∆ xk = xk – xk-1	, имеем:

σ = (x1 – x0) + (x2 – x1) + (x3 – x2) + ... + (xn-1 – xn-2) + (xn – xn-1) = b – a.

	b
Следовательно,	∫	dx = lim σ = b − a .
	∫	λ → 0
	a

30. Свойства определенного интеграла. При рассмот-

рении свойств определенных интегралов предполагаем, что интегралы, входящие в доказываемые формулы, существуют.

1) По определению полагаем, что

∫ f (x )dx = 0

b a

∫ f (x )dx = − ∫ f (x )dx .

a b

Первое равенство обусловливается тем, что при составлении интегральных сумм в данном случае каждое из ∆ xk будет равно нулю и σ = 0.

2 2 9

Второе равенство объясняется тем, что, когда разбиение производится от b к а, то разности ∆xk = xk – xk-1 будут отличаться знаком от таких же разностей в случае разбиения отрезка от а к b.

2) Постоянный множитель можно выносить за знак определенного интеграла, т.е.

b	b
∫kf (x )dx =	k ∫ f (x )dx, k = const .
a	a

Доказательство. Построим интегральную сумму для функции kf (x) на отрезке [a; b]:

	σ = ∑n	kf (ξ k )∆x k .
	k =	1
Очевидно, ∑n	kf (ξ k )∆x k	= k ∑n	f (ξ k )∆x k .
k = 1		k =	1

Тогда, пользуясь определением определенного интеграла, имеем

b	lim ∑n
∫ f (x )dx =	lim ∑n	kf (ξ k )∆x k =
a	λ → 0 k = 1

= lim k ∑n			∑n		b
= lim k ∑n	f (ξ k )∆x k = k lim		∑n	f (ξ k )∆x k = k ∫ f (x )dx .
λ → 0 k = 1		λ → 0 k = 1			a
3) Определенный интеграл от суммы функций равен сумме их
интегралов, т.е.
b			b		b
∫(g(x ) +		f (x )) dx =	∫ f (x ) dx +		∫g(x ) dx .	(4)
a			a		a

Доказательство. Действительно, построив интегральную сумму для f + g на отрезке [a; b], имеем

σ f + g = ∑n	( f (ξ k ) + g (ξ k )) ∆ xk = ∑n		f (ξ k )∆ xk + ∑n		g (ξ k )∆ xk = σ f + σ g .
k =	1	k =	1	k = 1
Остается перейти к пределу при λ →				0 и получим равенство (4).
4) Если c (a; b), то
	b	c		b
	∫ f (x ) dx =	∫ f (x ) dx +		∫ f (x ) dx .	(5)
	a	a		c

Доказательство. Рассмотрим произвольное разбиение отрезка [a; b], такое, чтобы точка с была точкой разбиения, например, c=xm. Будем иметь:

2 3 0

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 2223 / 4123 24 25 26 27 28 29 30 31 32 33 34 35 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.11.2018253.44 Кб9второй курсач(разработка)(Кристина)2.doc
#
13.09.201940.04 Кб6Вуліца Замкавая.docx
#
18.02.2016147.97 Кб2вучэбная праграма 2012.doc
#
19.02.201612.77 Mб65Высшая матем. Учебник.pdf
#
22.09.2019956.93 Кб18Высшая математика (1).doc
#
18.02.20165.88 Mб72высшая математика.pdf
#
18.02.2016192.33 Кб16Вычеты аналитических функций..pdf
#
18.02.2016190.98 Кб4гістарычная навука Бел. раб. праграма 2012.doc
#
14.04.2019380.93 Кб13Гісторыя Беларус(шпоры).doc
#
12.11.2019311.93 Кб3Гісторыя беларускага сялянства. Т.2..docx
#
15.04.2019130.2 Кб4гістрыя вся.docx