
высшая математика
.pdf Лекция 25
Лекция 25
Непрерывные функции
Вводятся понятия непрерывной функции в точке, на отрезке. Изучаются точки разрыва функции. Рассматривается непрерывность элементарных функций.
Из всего множества функций целесообразно выделить функции, обладающие свойством непрерывности. Грубо говоря, функция непрерывна, если ее график представляет сплошную линию, т.е. не имеет разрывов. Непрерывные функции обладают рядом интересных свойств.
Пусть функция f определена в некоторой окрестности точки х = а.
Функция f называется непрерывной в точке а, если lim f (x) = f( a) ,
x→ a
т.е. предел функции и ее значение в точке а равны.
Например, функция y = sign x является непрерывной x R, x ≠ 0. В точке х = 0 она не является непрерывной, так как не существует предела функции sign x в точке х = 0 (см. лекцию 23, рис. 1б).
Если lim |
f (x) = |
f( a) |
, то функция f называется непрерывной в |
x→ a+ 0 |
|
|
f (x) = f( a) , то – непрерывной в точке а |
точке а справа; |
если |
lim |
|
слева. |
|
x→ a− |
0 |
|
|
|
Теорема 1.
Для того, чтобы функция f была непрерывной в точке а, необходимо и достаточно, чтобы она была непрерывной в этой точке справа и слева.
Эта теорема является по существу переформулированной теоремой 1 из предыдущей лекции.
Приведем еще одно определение непрерывной в точке функции.
По первому определению имеем, что |
lim f (x) = f( a) . |
||
|
x→ |
a |
|
Это неравенство равносильно следующему: lim( f (x) − f( a) ) = 0 . |
|||
Если учесть, что соотношения |
x → |
x→ |
a |
a и (x – a) → |
0 также равно- |
||
сильны, то получим, что условие непрерывности функции f в точке а запишется в виде
lim ( f (x) − f( a) ) = 0 . |
(1) |
x− a→ 0 |
|
151
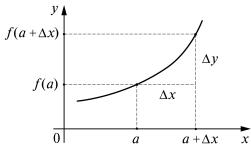
Рис. 1
Разность х – а называют приращением независимой переменной х
в точке |
а |
и |
обозначают |
через |
∆ x, ∆ x = x − |
a , |
а |
разность |
|
f (х) – f (а) |
– |
приращением функции |
f в точке |
а и |
обозначают |
||||
∆ y, ∆ y = |
f (x) − |
f( a) . Теперь условие (1) можно записать так: |
|||||||
|
|
|
lim ∆ y = |
0 . |
|
|
|
|
|
|
|
|
∆ x → 0 |
|
|
|
|
|
|
Заметим здесь, что x = a + |
∆ x |
и f (a + ∆ x) = f( a) + ∆ |
y . |
|
|||||
Тогда новое определение непрерывности функции в точке будет |
|||||||||
следующим. |
|
|
|
|
|
|
|
|
|
Функция f |
называется непрерывной в точке а, если ее приращение |
||||||||
в этой точке есть БМФ. |
|
|
|
|
|
|
|||
Геометрический смысл этого определения вытекает из рис. 1 |
|||||||||
(сравните с рис. 1б лекции 23). |
|
|
|
|
|
|
|||
Функция f |
называется непрерывной на интервале (а, b), если она |
||||||||
непрерывна в каждой точке x |
(a; b). Если же, кроме того, |
функция f |
|||||||
непрерывна в точке а справа, а в точке b – слева, то |
функция |
||||||||
f называется непрерывной на отрезке [а; b].
Точка а называется точкой разрыва функции f, если функция f не является непрерывной в этой точке.
Точки разрыва подразделяются на два типа.
К точкам разрыва 1-го рода относят такие точки разрыва функции f, в которых она имеет односторонние пределы, но они не равны
между собой, lim |
f (x) ≠ |
lim |
f( x) . |
x→ a+ |
0 |
x→ a− |
0 |
Так, функция sign x в точке х = 0 имеет разрыв первого рода. Точки разрыва 2-го рода составляют такие точки, в которых y
функции f не существует хотя бы одного из односторонних пределов.
152
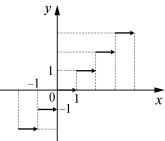
|
|
|
Рис. 2 |
|
|
Например, для функции |
y = |
1 |
точка х = 0 является точкой разрыва вто- |
||
x |
|||||
|
|
|
|
||
рого рода, так как lim |
f (x) = |
+∞ , lim |
f( x) = −∞ . |
||
x→ a+ 0 |
|
|
x→ a− |
0 |
|
Функция f называется кусочно непрерывной на отрезке
[а; b], если она непрерывна во всех внутренних точках [а; b], за исключением конечного числа точек, в которых она имеет разрывы первого рода, а в точках а и b имеет соответствующие односторонние пределы. Примером кусочно непрерывной функции является функция y = [x] (рис. 2).
Теорема 2.
Пусть функции f и g непрерывны в точке х = а. Тогда функции
f ± g, f ×g, |
|
f |
|
также непрерывны в этой точке (последняя при усло- |
||
|
g |
|||||
|
|
|
|
|
||
вии, что |
g (a) ≠ 0). |
|
|
|||
Действительно, пусть f и g непрерывны в точке а. Тогда |
||||||
lim f (x) = |
f( a) |
и lim g(x) = g( a) |
. Следовательно, |
|||
x→ a |
|
|
|
x→ a |
|
|
|
|
|
|
lim( f (x) + g( x) ) = |
lim f( x) + |
lim g( x) = |
|
|
|
|
x→ a |
x→ a |
x→ a |
= f (a) + g( a) = ( f( x) + g( )x ) |x= a .
Аналогично рассматриваются остальные случаи.  Справедлива также теорема о непрерывности сложной функции.
Справедлива также теорема о непрерывности сложной функции.
153

Теорема 3.
Пусть функция у = f (х) непрерывна в точке x0, а функция z = g (y) непрерывна в точке y0, y0 = f (x0).Тогда сложная функция g (f (x)) непрерывна в точке x0.
Другими словами, суперпозиция непрерывных функций есть функция непрерывная.
|
Доказательство. Возьмем произвольную последовательность |
||||||||||||
точек {xn |
}, lim xn |
= x0 . |
Тогда из непрерывности функции f в точке x0 |
||||||||||
|
|
|
x→ ∞ |
|
|
|
|
|
|
|
|
|
|
следует, |
что |
lim f (x) = f( x0) |
|
и |
lim f (xn ) |
= f( x0) . Обозначим |
|||||||
f (x |
) = y |
|
|
x→ x0 |
|
|
|
|
= |
x→ |
∞ |
как функция g непре- |
|
, n N. Получим, что lim y |
n |
y |
0 |
. Так |
|||||||||
n |
n |
|
|
|
x→ |
∞ |
|
|
|
|
|
||
рывна в точке y0, то |
lim g(y) |
= |
g( y0) |
, |
и по определению предела |
||||||||
lim g(yn ) |
= g( y0) |
|
y→ y0 |
|
|
|
|
|
|
|
|
||
. Если учесть, что yn = f (xn), то будем иметь, что для |
|||||||||||||
n→ ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
любой последовательности {xn }, |
сходящейся к x0, соответствующая |
||||||||||||
последовательность {g( f (xn ))} сходится к g (f (x0). |
|||||||||||||
|
Следовательно, |
lim g( f (x)) = |
|
g( f( x0)) . |
|
||||||||
|
|
|
|
x→ x0 |
|
|
|
|
|
|
|
|
|
|
Теорема 3 |
доказана. |
|
|
|
|
|
|
|
|
|||
|
Справедлива также |
|
|
|
|
|
|
|
|
||||
Теорема 4 (о непрерывности обратной функции).
Пусть функция у = f (x) строго монотонна и непрерывна на промежутке Х и пусть Y – множество ее значений. Тогда на множестве Y существует обратная функция x = f–1 (y), непрерывная и строго монотонная на Y.
Интересно, являются ли элементарные функции непрерывными. Рассмотрим вначале простейшие элементарные функции.
1) Постоянная функция f (x) =c является непрерывной в каждой
точке числовой прямой. Действительно, |
a R lim f (x) = c = |
f( a) . |
|
x→ a |
|
Непрерывной на всей числовой прямой является и функция |
||
f (x) = х. Действительно, a R lim x = a . Отсюда по теореме 2 полу- |
||
x→ a |
|
|
чим, что степенная функция f (x) = хn (n |
N) непрерывна на R, |
так как |
xn есть произведение n функций f (x) = х. |
|
|
154 |
|
|

Следовательно, по той же теореме 2 многочлен
f (x) = a0 xn + a1 xn–1 +...+ an–1 x + an
есть функция, непрерывная на R.
Рациональная функция R(x) = p((x)) , где p и q – многочлены, есть q x
также непрерывная функция всюду на R, за исключением тех точек, в которых знаменатель, многочлен q(х), обращается в нуль.
2) Тригонометрические функции sin x, cos x являются непрерыв-
ными на R. Рассмотрим, например, функцию sin x. Тогда a R будем иметь:
|
|
|
|
|
(a + |
∆ x) − |
|
|
|
|
|
|
|
|
|
|
|
∆ x |
|
|
sin |
∆ x |
|
|||||||||||||
|
∆ y = |
|
sin |
sin a = 2 cos |
|
a |
+ |
|
|
|
|
|
|
|
; |
|||||||||||||||||||||
|
|
2 |
|
2 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ x |
|
|
|
∆ x |
|
|
|
|
|
|
|
|
|||||||
|
|
lim ∆ y = |
2 lim cos a |
+ |
|
|
|
sin |
|
|
|
|
|
= |
|
0 |
, |
|
|
|
||||||||||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
||||||||||||||||||||||||||
|
∆ x→ 0 |
|
|
|
|
|
∆ x→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
∆ x |
|
|
|
|
|
|
|
|
∆ x |
|
|
|
|
|
sin |
∆ x |
|
|
∆ x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||
так как |
cos a |
+ |
|
|
|
|
≤ |
1, |
а |
lim sin |
|
|
|
= |
|
lim |
|
|
|
|
|
|
|
|
|
|
= |
|||||||||
2 |
|
|
2 |
|
|
|
∆ x |
2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∆ x→ |
0 |
|
|
|
|
∆ x→ 0 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
sin |
∆ x |
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
= |
lim |
2 |
|
lim ∆ x = |
1 0 = |
0 . |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
∆ x |
|
2 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
2 ∆ x→ |
0 |
|
|
∆ x→ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тригонометрические функции tg x и sec x являются непрерывны- |
||||||||||||||||||||||||||||||||||||
ми во всех точках, где cos x ≠ 0, т.е. x ≠ π |
|
/ 2 + π n, n |
Z, а функции ctg x, |
|||||||||||||||||||||||||||||||||
coseс x – |
во всех точках, где sin x ≠ 0, т.е. x ≠ π |
|
|
n, n |
Z. |
|||||||||||||||||||||||||||||||
3) |
Можно |
|
также |
доказать, |
|
что |
|
|
функции f (x) = ax и |
|||||||||||||||||||||||||||
f (x) = loga x (a > 0, a ≠ |
|
1) также являются непрерывными в области свое- |
||||||||||||||||||||||||||||||||||
го существования (первая – на R, |
вторая – на (0, +∞ |
)). |
||||||||||||||||||||||||||||||||||
Исходя из определения элементарных функций и теоремы 3 о непрерывности сложной функции, можно доказать следующую теорему.
Теорема 5.
Любая элементарная функция, определенная в окрестности некоторой точки, непрерывна в этой точке.
155

Иначе говоря, элементарные функции непрерывны в области своего существования.
Пример 1. Исследовать на непрерывность функцию f (x) = |
sin x |
. |
||||
|
x |
|
||||
|
|
|
|
|
||
Решение. Пусть x > 0.Тогда f (x) = |
sin x |
, и рассматриваемая |
||||
|
x |
|
|
|
|
|
функция будет непрерывной, как частное двух непрерывных функ-
ций. Если же x<0, то |
f (x) = |
− |
sin x |
, и функция f |
непрерывна и на |
|||||
x |
||||||||||
|
|
|
|
|
|
|
|
|
||
промежутке (–∞ |
; 0). Осталось исследовать функцию в точке х = 0. |
|||||||||
|
|
sin x |
|
|
|
|
sin x |
|||
Имеем lim f (x) = lim |
|
= |
1, |
lim |
f (x) = lim − |
|
|
= − 1 . |
||
x |
x |
|
||||||||
x → + 0 |
x → + 0 |
|
|
x → − 0 |
x → − 0 |
|
|
|||
Таким образом, в точке х=0 функция f имеет разрыв 1-го рода.
|
|
|
|
|
|
|
|
1 |
|
|
|
Пример 2. Исследовать на непрерывность функцию f (x) = e |
|
. |
|||||||
x |
||||||||||
|
|
Решение. Функция f представляет собой сложную функцию |
||||||||
u = |
1 |
|
и f (u) = eu. |
|
|
|
||||
x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция u = |
1 |
непрерывна всюду на R, за исключением точки |
||||||
|
|
|
||||||||
|
|
|
|
|
|
x |
|
|
|
|
х = 0, |
|
а функция f(u) непрерывна на R. |
Значит, сложная функция |
|||||||
|
|
1 |
непрерывна в каждой точке x |
R, x ≠ 0. |
||||||
f (x) = e |
x |
|||||||||
Исследуем эту функцию в точке х = 0:
11
lim e |
x |
= 0, |
lim e |
x |
= +∞ . |
x → − 0 |
x → + 0 |
||||
Следовательно, точка х = 0 является точкой разрыва 2-го рода. 
! Задания для самостоятельной работы
1. Показать, что функция y = |x| непрерывна на R.
156
|
|
|
|
|
sin x |
|
|
2. Показать, что функция |
f (x) = |
|
, если |
x ≠ 0, |
|||
x |
|||||||
|
|
|
|
|
0 |
||
|
|
|
|
1, если x = |
|||
непрерывна на R. |
|
|
|
|
|
|
|
3. Функция f задана формулами: |
|
|
|||||
|
x 2 − |
9 |
|
|
|
|
|
f (x) = |
|
|
, если |
|
x ≠ |
3, |
|
x − |
3 |
|
|
||||
|
|
|
|
3. |
|
|
|
A, если x = |
|
|
|||||
Как следует выбрать число А, чтобы функция f была непрерывна в точке х = 3? Построить график функции f.
4. Установить, в каких точках и какого рода разрывы имеют следующие функции, и построить их графики:
а)
б)
в)
f (x) =
f (x) =
f (x) =
x + |
1, |
|
если x [0;1), |
|
||||||
|
3x |
+ 2, если x |
(1; 2]; |
|||||||
|
||||||||||
|
1− |
x 2 , |
если |
x |
,(− |
∞ |
; 0], |
|||
|
x, |
если x |
(0; + |
∞ |
]; |
|
||||
|
|
|||||||||
|
|
x + |
1, |
|
если |
x |
, (− |
∞ |
; 0], |
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
, |
если x |
(0;1) (1; + ∞ ) . |
|||||
|
|
|
|
|||||||
|
− |
x |
||||||||
|
1 |
|
|
|
|
|
|
|||
5. Исследовать на непрерывность следующие функции:
а) y = |
x2 |
|
; б) y = |
ln (cos x) ; в) y = |
(1+ x)arctg |
1 |
. |
|
x − |
2 |
1− x2 |
||||||
|
|
|
|
|
157
 Лекция 26
Лекция 26
Функции, непрерывные на отрезке. Эквивалентные функции
Изучаются основные свойства непрерывных на отрезке функций. Вводится понятие эквивалентных БМФ, рассматриваются их свойства и важнейшие примеры.
10. Теорема 1 (об устойчивости знака непрерывной функции) .
Пусть функция f непрерывна в точке а, и f (a) ≠ 0. Тогда существует δ-окрестность точки а такая, что в этой окрестности функция f имеет тот же знак, что и f (a).
Доказательство. Пусть, например, f (a) > 0.Тогда по определению непрерывности lim f (x) = f( a) . Возьмем ε= f (a). По определению
x→ a |
x, 0 < |x – a| < δ будет |
предела для данного ε= f (a) δ > 0 такое, что |
выполняться неравенство |f (x) – f (a)| < ε. Последнее неравенство можно переписать следующим образом:
–f (a) < f (x) – f (a) < f (a) или 0 < f (x) < 2f (a).
Таким образом, x (a – δ; a + δ) имеем, что f (x) > 0. Теорема 1 доказана. 
Геометрический смысл этой теоремы состоит в том, что, если функция f непрерывна в точке а и отлична в ней от нуля, то некоторая часть графика этой функции, проходящая через точку (a; f (a)), не пересекает ось x (рис. 1).
Теорема 2 (первая теорема Больцано-Коши).
Пусть функция f непрерывна на отрезке [a, b] и на концах отрезка имеет значения разных знаков. Тогда существует точка c (a; b), в которой f (c) = 0.
Геометрический смысл этой теоремы также очевиден. Поскольку функция f непрерывна на отрезке, то ее график состоит из одного «сплошного» куска. Эта кривая соединяет точки (a; f (a)), (b; f (b)), одна из которых лежит ниже оси Ох, вторая – выше оси Ох. Следовательно, существует точка с на оси Ох, в которой график пересекает ось Ох (рис. 2).
158
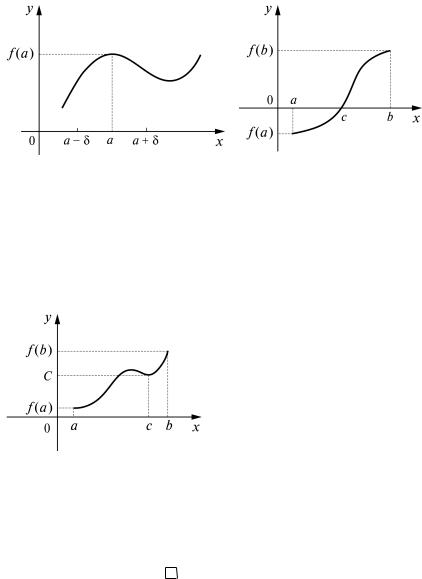
Рис. 1 Рис. 2
Теорему 2 легко обобщить. Справедлива
Теорема 3 (вторая теорема Больцано-Коши).
Пусть функция f непрерывна на отрезке [a; b], причем f (a) ≠ f (b). Тогда если С – любое число, лежащее строго между f (a) и f (b), то существует точка с (a; b) такая, что f (с) = С.
|
|
Другими словами, теоре- |
|
|
ма 3 утверждает, что непрерыв- |
|
|
ная на отрезке [a; b] функция |
|
|
принимает любое свое проме- |
|
|
жуточное значение. |
|
|
Геометрический смысл |
|
|
этой теоремы также очевиден |
|
|
(рис. 3). |
|
|
Доказательство теоремы |
|
Рис. 3 |
3 опирается на теорему 2. |
пример, f (a) < f (b) и f (a) < С < f (b). |
Действительно, пусть, на- |
|
Тогда рассмотрим функцию |
||
ϕ |
(x)=f (x) – С. Эта функция непрерывна на отрезке [a; b] и ϕ (a) =f(a) – С<0, |
|
ϕ |
(b) = f (b) – С > 0. Следовательно, к функции ϕ можно применить пер- |
|
вую теорему Больцано-Коши. В соответствии с ней получим, что суще-
ствует точка c |
(a; b) такая, что ϕ (c) = 0, т.е. f (c) – C = 0, f (c) = C. |
Теорема 3 доказана. |
|
Теорема 4 |
(первая теорема Вейерштрасса). |
Если функция f непрерывна на отрезке [a, b], то она ограничена.
159
Таким образом, в теореме 4 утверждается, что если функция f непрерывна на отрезке [a; b], то существует число M > 0, такoе, что
x [a; b] : | f (x)| ≤ M.
Доказательству теоремы предпошлем следующую лемму.
Л е м м а .
Функция f, непрерывная в точке а, ограничена в некоторой окрестности этой точки.
Действительно, по определению lim f (x) = f( a) . Пусть ε= 1. Тог-
x→ a
да для этого числа ε существует число δ > 0, такое, что x (a – δ; a + δ) : | f (x) – f (a)| < 1.
Полученное неравенство можно записать в виде
–1 < f (x) – f (a) < 1 или –1 + f (a) < f (x) < f (a) + 1.
Положим M = f (a) + 1. Тогда x (a – δ; a + δ) : | f (x) | < M.
Лемма доказана.
Доказательство теоремы 4. Предположим противное. Пусть функция f является неограниченной на отрезке [a; b]. Разделим отрезок [a; b] пополам. Тогда, по крайней мере, на одном из полученных двух отрезков функция f неограничена. Обозначим его через [а1; b1] . Далее делим отрезок [а1; b1] пополам. Функция f снова на одном из полученных отрезков неограничена. Обозначим соответствующий отрезок через [а2; b2]. Продолжая этот процесс, получим последовательность отрезков [a; b], [а1; b1], [а2; b2], ...,[аn; bn], ..., вложенных друг
в друга, b |
− |
a |
n |
= |
b − a |
→ |
0 при n → ∞ |
. Причем на каждом из этих |
|
||||||||
|
n |
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
отрезков функция f неограничена. По теореме 4 лекции 22, существует единственная точка х = с, принадлежащая всем этим отрезкам. Функция f непрерывна в этой точке и, следовательно, по лемме ограничена в некоторой ее окрестности. А это противоречит тому, что функция f неограничена на каждом отрезке [an; bn], n N . Теорема 4 доказана. 
Заметим, что если в теореме 4 вместо отрезка [a; b] рассматривать интервал (а; b) или какой-либо полуинтервал, то функция f может быть и неограниченной, т.е. в этом случае утверждение об ограничен-
ности несправедливо. |
Например, функция f (x) = |
1 |
непрерывна на |
|
x |
||||
полуинтервале (0; 1], |
но не ограничена на нем. |
|
||
|
|
160
