Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

высшая математика

.pdf

Скачиваний:

Добавлен:

18.02.2016

Размер:

5.88 Mб

Скачать

☆

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 4119 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

(n − 1)

n(n − 1)

(n −

) =

sin

x +

n sin x

2x +

sin x +

2 =

sin

x +

2nx sin x +

(n − 1)

n(n − 1)sin x + ( n −

40. Применения производной в экономике. Пусть фун-

кция

I = I (x)

характеризует зависимость издержек производства от ко-

личества выпускаемой продукции. Предположим, что количество про-

дукции увеличивается на ∆ x , т.е.	равно x + ∆ x , соответствующие
издержки производства будут равны	I (x + ∆ x) .
Тогда приращению количества продукции ∆ x соответствует
приращение издержек производства продукции
I (x + ∆ x) − I( x) = ∆ I( x) .
Среднее приращение издержек производства будет равно		∆ I (x)	.

		∆ x

Это есть приращение издержек производства на единицу приращения количества продукции. Если перейти к пределу, когда ∆ x → 0 , то получим значение предельных издержек производства

lim	∆ I (x)		=	′

	∆	x		I (x) .
∆ x→ 0

Аналогично, если выручка от реализации х единиц товара описывается функцией W = W (x), то предельная выручка определяется как

lim	∆ W (x)	′

	∆ x	= W (x) .
∆ x → 0

Подобным образом в экономике определяются другие предельные понятия. Например, широко применяется понятие эластичности функции. Эластичностью функции у = f (х) относительно переменной х называется величина

Ex (y) =	x	′	(9)

	f (x) f (x) .

Эластичность функции характеризует процент прироста зависимой переменной, соответствующий приращению независимой переменной на 1%.

181

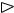
Пример 5. Найти эластичность функции y = x3 + 2. Решение. Применяя формулу (9), имеем

Ex (y) =

(x3

2)′=

3x3

x3 +

В частности, если,

например, х = 2,

то

Ex (y) =

3 8

2,4 .

8 + 2

Это означает, что если переменная х возрастает на 1%, то переменная у увеличится на 2,4%.

! Задания для самостоятельной работы

1. Найти производные следующих функций:

а) y = x4x; б) y = xsinx; в) y = (ln x)cosx.

2. Найти производные от следующих функций у=у(х), заданных неявно:

а) x	3	+ y	3	= 0; б)	x2	+	y2	= 1; в) 1 + ln (x	2	+ 2xy + 1) = 0.
					a2		b2

3. Найти производные указанного порядка от данных функций:

а) y = cos(2x +

в) y = lg (sin x)

г) y = x3 cos x,

1) , y′– ? б) y = e3x+ 1, y(4) (0) – ? , y′– ?

y(n) – ? д) y = x2ex , y(5) – ?

4. Рассчитать эластичность следующих функций и найти значения эластичности для указанных х:

а) y = sin 2x,	x =	π	; б) y = x3 + x + 1, x = 2; в) y = 4 ln x, x = e2.
		3

182

Лекция 30

Дифференциал функции. Теоремы о среднем

Вводится понятие дифференцируемой в точке функции. Устанавливается его связь с существованием производной. Дается определение дифференциала функции, рассматриваются применения дифференциала в приближенных вычислениях. Приводятся основные теоремы дифференциального исчисления.

10. Понятие дифференцируемости функции в точке.

Выше указывалось, что операция нахождения производной называется дифференцированием. Применение этого термина оправдано следующими рассуждениями.

Функция y = f (x) называется дифференцируемой в точке х, если ее приращение y в этой точке можно представить в виде

∆ y = A∆ x + α (∆ x)∆ x ,

(1)

где А – некоторое число, не зависящее от ∆ x, α (∆ x) – БМФ при

∆ x → 0 .

Теорема 1.

Для того, чтобы функция y = f (x) была дифференцируемой в точке х, необходимо и достаточно, чтобы она имела в этой точке производную f ′(x) .

Доказательство. Необходимость. Пусть функция y = f (x) дифференцируема в точке х. Тогда справедлива формула (1). Разде-

лим обе части этого равенства на ∆ x				и получим
	∆ y	=	A + α (∆	x) .
	∆ x

По теореме 7 из Л.24 это означает, что существует

lim	∆ y	=	′

	∆ x		A, т.е. f (x) = A .
∆ x→ 0

Достаточность. Предположим, что функция y =f (x) имеет производную в точке х, т.е. существует

183

lim

∆ y

= f ′(x) .

∆ x→ 0

∆ x

Тогда по той же теореме 7 из Л.24 имеем

∆ y

′

∆ x =

f (x) + α ( ∆ x) ,

где α (∆ x) – БМФ при ∆ x →

0 . Отсюда находим, что

∆ y =

′

f (x) ∆ x + α ( ∆ x) ∆ x ,

т.е. функция y =f (x)

дифференцируема в точке х.

′

Таким образом, в формуле (1) можно положить A = f (x) .

20. Дифференциал функции и приближенные вы-

числения

помощью

дифференциала.

Пусть

функция

y = f (x)

дифференцируема в точке х. Тогда приращение функции в

этой точке может быть записано по формуле (1) в виде

где lim α (∆ x) =

∆ y =

A ∆ x + α (∆ x) ∆ x ,

(2)

0 . Второе слагаемое

α (∆ x) ∆ x является БМФ более

∆ x→

высокого порядка по сравнению с функцией A ∆ x (при условии, что

A ≠ 0),

lim

(∆

x)∆

= lim

(∆ x)

= 0 . Поэтому первое слагаемое

A∆ x

A ∆ x

∆ x→ 0

∆ x→

является главной частью приращения ∆ y ,

причем это слагае-

мое есть линейная относительно ∆ x функция.

Главная,

линейная

относительно

∆ x часть приращения функции ∆ y

в точке х называ-

ется дифференциалом функции y = f (x)

в этой точке. Для обозначения

дифференциала используется символ

dy = A ∆ x .

Если А = 0,

то

A ∆ x

не является, вообще говоря, главной час-

тью приращения ∆ y . В этом случае по определению полагают dy = 0.

Учитывая теорему 1, а именно, что A =		′
		f (x) , можно записать, что
dy =	′	(3)
	f (x) ∆ x .

Теперь найдем дифференциал функции f (x) = x. Применяя формулу (3), имеем

dy = (x)′∆ x = ∆ x .

Поэтому определяют дифференциал независимой переменной х

184

следующим образом: полагают dx = ∆ x . Тогда формулу (3) можно записать в виде

dy = f ′(x) dx .

	Заметим, что производную функции y = f (x) обозначают			dy	или
	Заметим, что производную функции y = f (x) обозначают			dx	или
	df (x)			dx
	df (x)	.
	dx
	Обратимся снова к формуле (2). На основании вышеизложенного
можно записать, что ∆ y ≈dy			или
		f (x + ∆ x) −	′		(4)
		f (x + ∆ x) −	f( x) ≈ f ( x) ∆ x .		(4)

Формула (4) часто используется в приближенных вычислениях. Покажем ее применение на следующих примерах.

Пример 1. Найти приближенное значение e0,2.

Решение. Воспользуемся формулой (4). Очевидно, в данном

случае f (x) = ex. Положим х = 0,		∆ x = 0,2 .
Будем иметь:		′
Будем иметь:	ex+ ∆ x − ex ≈(ex ) ∆ x или
e0,2 −	e0 = e0 0,2,	e0,2 ≈1+ 0,2 =	1,2.
Итак, e0,2 ≈1,2. Более того,		при малых ∆ x	и x = 0 мы получим
формулу
	e∆ x ≈1+ ∆ x .		(5)
При применении формулы (4) важно правильно выбрать точку х
и ∆ x .

Пример 2. Найти приближенное значение sin 29°.

Решение. Нам известно значение sin 30°, равное 0,5. Воспользуемся

им и формулой (4). В качестве ∆ x

следует взять радианную меру 1°,

т.е. величину

2π

со знаком минус.

Имеем

360

180

sin(x + ∆ x) −

sin x ≈cos x ∆ x ,

x =

∆ x = −

180

Поэтому получим,

что

sin 290

≈sin

− cos π

1 −

≈0,4849 .

180

185

30. Теоремы о среднем. Рассматриваемые в этом пункте теоремы о среднем значении называют еще основными теоремами о дифференцируемых функциях.

Говорят, что функция y = f (x) имеет в точке xo локальный максимум (минимум), если существует δ–окрестность (xo – δ; xo + δ) такая, что

	x	(	0	δ ;+x	a		)	( )	(	0)	(	( )	( )	0	)	.
	x		x−	δ ;+x		δ		: f ≤ x	f x			f≥ x	f x			.

Локальный максимум и локальный минимум объединяются общим термином – локальный экстремум. Локальными называются свойства функции, которые имеют место в некоторой окрестности той или другой точки.

Теорема Ферма.

Пусть функция f определена на интервале (a; b) и в некоторой точке xo (a, b) имеет локальный экстремум. Тогда, если в точке xo существует производная, то она равна нулю, т.е. f ′(x0 ) = 0 .

Рис. 1

Теорема Ролля.

Геометрический смысл теоремы Ферма состоит в том, что если в точке x0 (a, b) функция имеет локальный минимум или максимум (рис. 1), то касательная в этой точке к графику функции y = f (x) параллельна оси Ох, т.е. угол наклона касательной к оси

Ох равен нулю, и f ′(x0 ) = tg 0 = 0 .

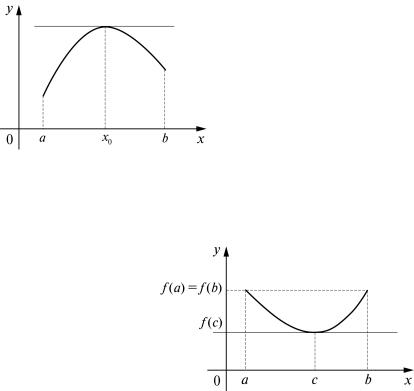
Пусть функция f непрерывна на отрезке [a; b], дифференцируема

на интервале (a; b) и на
концах отрезка [a; b] при-
нимает равные значения,
f (a) = f (b), то существу-
ет точка c	(a; b), в кото-
′	0 .
рой f (с) =

Г е о м е т р и ч е с к и й
смысл этой теоремы зак-
лючается в том, что у гра-
фика непрерывной на от-	Рис. 2
	Рис. 2

186

Рис. 3

резке [a; b] функции, принимающей на концах равные значения и дифференцируемой на (a; b), существует точка (с; f (с)), в которой касательная параллельна оси Ох.

Иначе говоря, такая функция внутри отрезка [a, b] будет иметь экстремум (например, в точке c (a; b)) и по теореме Ролля f ′(с) = 0 .

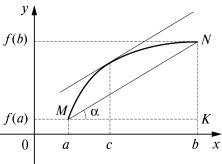
Теорема Лагранжа.

Если функция f непрерывна на отрезке [a; b], дифференцируема на интервале (a, b), то существует точка c (a; b), такая, что справедлива формула:

f (b) −	f( a)	=	′			(6)
b −	a	=	f (c) .			(6)
b −	a
			Рассмотрим			геометри-
			ческий смысл теоремы Лаг-
			ранжа.
			Из ∆ MKN			имеем, что
				NK		f (b) − f( a)	,
			tg α = MK		=	b − a

т.е. левая часть равенства (6) есть тангенс угла наклона секущей MN к оси Ох. Правая часть равенства (6) есть тангенс угла наклона касательной в некоторой

точке c (a; b). Таким образом, теорема Лагранжа утверждает, что найдется точка c (a; b), в которой касательная к графику функции параллельна секущей, соединяющей концы графика функции (точки

(a; f (a)) и (b; f (b)).

Соотношение (6) можно записать в виде:

	f (b) −	f( a) = f ( c)( b − )a .	(7)
		′
Формулу (7) называют формулой конечных приращений.
Теорема	Коши.
Если функции f и g непрерывны на отрезке [a; b], дифференциру-
емы на	интервале (a; b),	′	то существует точка
емы на	интервале (a; b),	причем g (x) ≠ 0 ,	то существует точка
c (a; b),	такая, что справедливо равенство:

187

		f (b) − f( a) =			f ′(c) .
						′
		g(b) − g( a)			g (c)
Пример 2.	Найти дифференциал функции y = x2 + 2x + 2 в точке
х = 1 двумя способами:			линейную относительно ∆ x
а) выделяя главную,								часть прира-
щения ∆ y ;
б) по формуле (3).
Решение. Придадим в точке х						приращение аргументу ∆ x и
найдем соответствующее			приращение функции ∆ y :
∆ y = f (x + ∆ x) − f( x) = ( x + ∆ x) 2 + 2( x + ∆ )x + 2 − (x2 + 2x + 2) =
= 2x ∆ x + (∆ x)2 + 2∆ x = 2( x + 1) ∆ x +( ∆ x) 2 .
Если x ≠ –1 , то главной,				линейной относительно ∆ x ,					частью
приращения	функции		∆ y	является величина 2(x + 1)					∆ x , т.е.
dy = 2(x + 1) ∆ x .	Заметим,		что в данном случае				α (∆ x) = (	∆ x)	2 .
Если искать дифференциал по формуле (3), то найдем:
f ′(x) = 2x + 2 = 2( x + 1) и dy = f(′x) ∆ x = 2( x + )1 ∆ x .
Если положить х = 1,			то dy = 4 ∆		x .
! Задания	для самостоятельной работы
1. Найти дифференциал функции						y = x3 + x2 + 1 в точке х = –1 дву-
мя способами:			линейную относительно ∆ x ,
а) выделяя главную,								часть прира-
щения функции ∆ y ;							α (∆ x) .
б) по формуле (3) напишите выражения для
2. Прямолинейное			движение			точки	задано	уравнением

s = 2t2 + t + 1, где время t выражается в секундах, а путь s – в метрах. Найти приращение и дифференциал пути s в момент времени t = 1c и сравнить их при :

а)

∆ t =

0,1c ;

б)

∆ t = 0,2c ;

в) ∆ t = 1c .

Найти дифференциал функции у в точке х, если:

а)

y =

x +

− 1

; б) y = xe

; в) y =

arctg

Используя формулу (4), найти приближенные значения:

а) cos 61o;

б)

3 1,01 ;

в) arctg 1,1;

г) arcsin 0,51;

д) lg 11.

188

Лекция 31

Правило Лопиталя. Формула Тейлора

С помощью теорем о среднем выводятся правила для эффективного нахождения пределов. Рассматривается одна из главных формул высшей математики – формула Тейлора.

10. Правило Лопиталя. Пусть функции f и g дифференцируемы в некоторой окрестности точки x = a, f (a) = g(a) = 0 и g′(x ) ≠ 0 при x ≠ a. Тогда, пользуясь теоремой Коши, можно записать:

f (x ) − f (a)

f ′(c)

g(x ) − g(a)

g′(c)

где точка c находится между точками x и a. Иначе говоря,

f (x )

f ′(c)

g(x )

g′(c)

Если x→ a , то c→ a и, следовательно, если существует lim

f ′(c)

g′(c)

c→

то существует и предел lim	f (x )	. Это утверждение и называют правилом

x → a g(x )

Лопиталя. Сформулируем его более строго в виде следующей теоремы.

Теорема 1 (правило Лопиталя).

Пусть функции f и g определены и дифференцируемы в некоторой окрестности точки а , за исключением, может быть, самой

точки а. Пусть функции f и g являются БМФ при x → a и								g′(x ) ≠ 0 в
окрестности точки а. Тогда, если существует lim						f ′(x )	,	то
окрестности точки а. Тогда, если существует lim						g′(x )	,	то
					x → a	g′(x )
lim	f (x )	=	lim	f ′(x )	.			(1)
lim		=	lim		.			(1)
x → a g(x )			x → a	g′(x )

Таким образом, в данном случае предел отношения двух БМФ сводится к пределу отношения их производных, что часто является весьма удобным приемом при вычислении пределов. Проиллюстрируем это на примере.

189

Пример 1. Найти предел lim sin 4x . x → 0 tg2x

Решение. В данном случае условия правила Лопиталя выполняются. Функции f (x) = sin 4x и g(x) = tg 2x являются дифференцируемыми

функциями, например, на интервале −

;

и f(0) = g(0) = 0. Приме-

ним формулу (1):

lim

sin 4x

lim

(sin 4x )′=

lim

4 cos 4x

2 lim cos 4x cos2 2x =

1/cos2 2x

x → 0 tg 2x

x → 0

(tg 2x )′

x → 0 2

x →

= 2 lim cos 4x lim cos2 2x =

2 .

x → 0

x →

Такимобразом,первоначальномыимеемнеопределенностьвида 00 ,послепере-

ходакпределуотношенияпроизводныхтакаянеопределенностьуже отсутствует. Если функции f и g дважды дифференцируемы в некоторой

окрестности

точки а,

f (a) =

g(a) =

f ′(a) = g′(a) = 0 и существует

lim

f ′(x )

, то имеет место равенство:

x → a g′(x )

lim

f (x )

lim

f ′(x )

g′(x ) .

x →

a g(x )

x →

Это означает, что если f ′(x )

g′(x ) , в свою очередь, являются

БМФ при x →

a, то правило Лопиталя применимо к пределу lim

f ′(x )

x → a

g′(x )

Нетрудносформулироватьусловия,прикоторыхсправедливаследующаяформула:


	lim	f (x )	=	lim		f (n) (x )		.		(2)

	x → a g(x )			x → a g(n) (x )
Пример 2.	Найти предел			lim	x −		sin x		.

				x → 0			x 3
Решение.	Функции f (x) = x – sin x и g(x) = x3									являются БМФ при

x → 0. Применяя правило Лопиталя, найдем:

190

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 4119 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.11.2018253.44 Кб9второй курсач(разработка)(Кристина)2.doc
#
13.09.201940.04 Кб6Вуліца Замкавая.docx
#
18.02.2016147.97 Кб2вучэбная праграма 2012.doc
#
19.02.201612.77 Mб65Высшая матем. Учебник.pdf
#
22.09.2019956.93 Кб18Высшая математика (1).doc
#
18.02.20165.88 Mб72высшая математика.pdf
#
18.02.2016192.33 Кб16Вычеты аналитических функций..pdf
#
18.02.2016190.98 Кб4гістарычная навука Бел. раб. праграма 2012.doc
#
14.04.2019380.93 Кб13Гісторыя Беларус(шпоры).doc
#
12.11.2019311.93 Кб3Гісторыя беларускага сялянства. Т.2..docx
#
15.04.2019130.2 Кб4гістрыя вся.docx