Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

высшая математика

.pdf

Скачиваний:

Добавлен:

18.02.2016

Размер:

5.88 Mб

Скачать

☆

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 4118 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

Лекция 28

Таблица производных основных элементарных функций. Производная сложной функции

Приводятся производные основных элементарных функций. Рассматриваются правила дифференцирования обратной и сложной функций.

10. Производная постоянной, степенной, тригонометрических и показательной функций.

		′			(C)		′
				т.е.			=	0 .
а) Пусть f (х) = С. Тогда f (x) = 0 ,
Действительно,
f ′(x) = lim	f (x + ∆ x) − f( x)		=	lim		C − C		= 0 .
						∆ x
∆ x → 0		∆ x		∆ x →	0
б) Пусть f (x) = xn, n		N .Докажем, что			f ′(x)		= n xn− 1 , т.е.

(xn )′= n xn− 1 .

Действительно, пользуясь биномом Ньютона,

∆ y = (x + ∆ x)

n− 1

(n − 1)

n− 2

(∆

− x

∆ x

n−

n (n − 1)

n−

∆ x + $+ (∆

−

= ∆

Следовательно,

)

′

∆ y

− 1

n (n −

n− 2

lim

lim nx

∆

x +

∆ x

∆ x → 0

∆ x →

так как

lim ∆

x =

0, lim

(∆

x)2

= 0,$, lim( ∆

n− 1 =

∆ x→

∆

x→

∆

x→ 0

получим

x)2 +	$+ (
x)n− 1 .

(∆ x)	=

n− 1

0 .

(1)

∆ x) n −

nx n− 1 ,

Заметим, что формула (1) имеет место при любом вещественном показателе степени, т.е. α R

(xα )′= α xα − 1 .

171

в) Производная функции

(sin x)′= cos x .

Докажем ее. Имеем, что

(sin x)′= lim	sin(x +	∆ x) − sin x	=
		∆ x
∆ x→ 0

y = sin x выражается формулой

			∆	x		∆ x
		2sin			cos x +
		2sin	2		cos x +	2
lim			2			2	=
lim					∆ x		=
∆ x→	0				∆ x

sin

∆ x

= lim

lim cos

x +

= 1 cos x =

cos x .

∆ x

∆ x→ 0

∆ x→

Первый предел вычислили исходя из первого замечательного пре-

дела, второй – исходя из непрерывности функции cos x.

Аналогично показывается,

что

(cos x)′=

− sin x .

На основании полученных формул и правила дифферен-

цирования частного имеем:

′

sin x

′

(sin x)

′

cos

x + sin

cos x −

( cos x) sin x

(tg x) =

;

cos2 x

cos2

cos x

(ctg x)′= −

sin 2 x

г) С помощью второго замечательного предела можно показать, что

(a x )′= a x ln a (a > 0, a ≠ 1) ;

(ex )′= ex .

20. Производная обратной функции.

Теорема 1.

Если функция у = f (х) строго монотонна и непрерывна в некоторой окрестности точки х0, имеет производную в точке x0 и f ′(x0 ) ≠ 0 , то обратная функция x = f –1 (y) имеет производную в соответству-

ющей точке y0, y0	= f (x0), причем (f − 1 (y0 ))′=		1	.
ющей точке y0, y0	= f (x0), причем (f − 1 (y0 ))′=	f	(x0)	.
			′

Доказательство. По теореме (см. теорему 4 Л.25) обратная функция x = f –1 (y) существует, является монотонной и непрерывной в

172

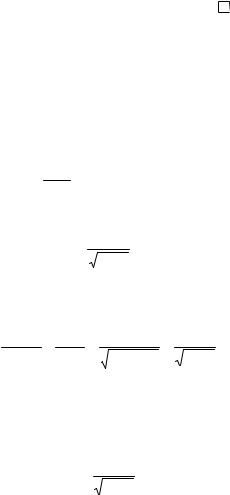
некоторой окрестности точки у0. Придадим аргументу у некоторое приращение ∆ y ≠ 0 в этой точке. Соответствующее приращение ∆ x в силу строгой монотонности тоже будет отличным от нуля.

∆ x

если ∆

y →

0 , то и ∆ x → 0 .

Следовательно,

, причем,

∆ y

∆ y / ∆ x

Перейдем к пределу в этом равенстве. Будем иметь

lim

∆ x

− 1

′

∆ y

lim

(∆ y / ∆ x)

или

(y0 )) =

f ′(x0 ) .

∆ y → 0

∆ x → 0

30. Производная

логарифмической

обратных

тригонометрических

функций.

а)

Производная функции y = logax (a > 0, a ≠

выражается фор-

мулой

(loga x)′=

x ln a

Действительно, логарифмическую функцию y = logax

можно рас-

сматривать как обратную показательной функции х = ау. Поэтому

(loga

x)′=

(a y )′=

a y ln a

x ln a

б)

Производная функции

y = arcsin x

выражается формулой

(arcsin x)′=

1 .

1−

Действительно, функция y = arcsin x является обратной для функции х = sin y. Поэтому, применяя правило дифференцирования обратной функции, будем иметь:

(arcsin x)′=	1	=	1	=	1	=	1	.
	(sin y)′		cos y		1− sin 2 y		1−	x2

Корень взят со знаком плюс, так как

y = arcsin x	−	π	;	π	и cos y > 0.
		2		2

Аналогично проверяются следующие формулы:

(arccos x)′= −		1	;
		1+	x2
(arctg x)′=		1		;
	+	x2
1

173

(arcctg x)′= − 1+ 1x2 .

Таким образом, найдены производные всех простейших элемен-

тарных функций, и можно составить следующую таблицу:

1) (c)′= 0 ;

′

α − 1

′

( x )

′

;

) = α x

= −

x 2

2 x

(a x )′= a x ln a (a > 0, a ≠ 1)

и (ex )′= ex ;

′

(loga x) =

0, a ≠ 1)

( ln x)

;

x ln a

5)(sin x)′= cos x ;

6)(cos x)′= − sin x ;

(tg x)′=

;

cos2 x

(ctg x)′=

−

;

sin 2 x

(arcsinx)

′

;

1−

(arccos x)′=

10)

−

;

1−

11)

(arctg x)′=

;

12)

(arcctg x)′=

−

40. Производная сложной функции.

Теорема 2.

Если функция u = ϕ

(x) имеет в точке х0 производную, а функция

y = f (u)

имеет в соответствующей точке u0, u0 = ϕ (x0), производную

′

, то сложная функция y = f (ϕ (x)) имеет производную в точке х0

f (u0 )

и справедлива следующая формула:

174

′

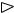
(2)

y (x0 )

f (u0)

ϕ (

x0) .

Доказательство. По определению производной

f ′(u0)

= lim

f (u0 +

∆ u) − f(u0)

lim

∆

f (u0)

∆ u

∆

→

∆

u→

∆ u

На основании теоремы 7 Л.24 можем записать, что

∆ f (u0 )

= f ′(u0 ) + α ( ∆ u) ,

∆ u

где α

(∆ u) есть БМФ при

∆ u →

0 .

Следовательно,

∆ f (u0 ) =

′

+ α ( ∆ u) ∆ u .

f ( u0) ∆ u

Разделив обе части этого равенства на

∆ x , получим

∆ f (u0 )

f ′(u

)

∆ u

+ α (∆ u)

∆ u

∆ x

Теперь перейдем к пределу,

когда

∆ x →

0 .

Заметив, что и

∆ u →

0 , будем иметь:

∆

f (u

)

f ′(u

)

∆ u

(∆ u)

∆ u

lim

∆

x→ 0

∆ x

∆ x→

∆

x→

∆ x

Остается учесть,

что

∆ f

(u0 )

′

∆ u

lim

( f

(ϕ (x0))) ,

lim

= ϕ

′(x0 ) ,

∆

∆ x→

(

∆ u

(

∆ u

lim

∆

lim

∆

lim

′

∆ x

(x0 )

∆ x → 0

∆ x

→

∆

x →

и получим формулу (2). Теорема 3 доказана. Формулы производных, приведенные выше в таблице, правила

дифференцирования суммы, разности, произведения, частного и правило дифференцирования сложной функции являются основными формулами дифференцирования функции. С их помощью можно найти производную любой элементарной функции.

Пример 1. Найти производную функции y = cos x + x arctg x + 2.

175

Решение. Вначале применим правило дифференцирования сум-

мы: y′= (cos x)′+ ( x arctg x) ′+( 2) ′.

Затем воспользуемся таблицей производных и правилом дифференцирования произведения:

	′	′		x
y′= − sin x + (x)	arctg x + x(arctg x)	+ 0	= − sin x + arctg x +		.
				(1+ x 2 )

Пример 2. Найти производные следующих функций:

a) y = sin (2x +	1) , б) y = ln3 x ,	в) y = ecos4 x .
Решение. а)	Данная функция	является сложной, y = sin u,

u = 2x + 1. Обе эти функции имеют производные, и по правилу дифференцирования сложной функции находим

y′=

′

cos u ×2 =

2 cos( 2x + )1 .

(sin u) ( 2x + 1)

б)

Имеем сложную функцию y = u3,

u = ln x .Получаем

′

= 3

ln2 x

) (ln x) =

в)

Имеем сложную функцию y = eu,

u = cos4 x .Получаем

y′= (eu )′(cos4 x)′= eu( cos4 x) ′.

Функция u = cos4 x в свою очередь является сложной u = v4,

v =

′

− 4sin x cos

x .

cos x; u =

)

(cos x)

4v ( − sin x)

Таким образом,

′

cos4

(−

4 sin x cos

x) =

−

2 sin 2x cos

x e

cos4 x

! Задания для самостоятельной работы

1. Найти производные следующих функций:

а)

y =

sin x ex ;

б)

y =

x +

;

в)

y =

tg x

;

г) y = 2cos x ;

ctg 2x

д)

y =

x +

;

е)

y =

x −

, a >

0 ;

ж)

y =

arccos x

;

x +

з)

y =

2 x

y =

x +

+ x

; и)

arctg

176

Лекция 29

Логарифмическое дифференцирование. Производная неявной функции. Производные высших порядков. Приложение производной

вэкономике

Приводятся метод логарифмического дифференцирования и правило дифференцирования неявной функции. Вводится понятие производной n-го порядка. Даются некоторые применения понятия производной в экономике.

10. Логарифмическая	производная. Предположим, что
f (x) > 0, x (a, b).
Рассмотрим функцию y = ln f (x). Дифференцируя эту функцию
как сложную, y = ln u, u = f (x),	получим
		′
′	′ ′	f (x)	(1)
(ln f (x)) = ( ln u) f ( x) =		f (x) .

Производная от логарифма функции называется логарифмической производной этой функции, а последовательное применение операции логарифмирования, а затем дифференцирования называется логарифмическим дифференцированием.

С помощью этого метода найдем, например, производную пока-

зательно-степенной функции y = (u (x))v (x),	где u, v – некоторые функ-
ции, имеющие в точке х производные,	u (x) > 0. Применяя формулу
(1), получим

yy′= [ln(u(x))v(x) ]′= [v(x)ln u( x) ]′.

В правой части имеем производную произведения:

	y′						u′(x)
		= v′(x) lnu( x) + v( x)							.
	y	= v′(x) lnu( x) + v( x)					u(x)		.
Следовательно,
			v x					u′(x)
y′= (u(x))			( )	v′(x)ln u( x)	+	v( x)				.	(2)
y′= (u(x))			( )	v′(x)ln u( x)	+	v( x)

									u(x)
Пример 1. Найти производную функции y = xx,											x > 0.

177

Решение. Если положить u = x и v = x , то можно применить формулу (2) и сразу записать производную. Мы же повторим рассуждения, использованные при выводе формулы (2). Рассмотрим ln y = x ln x .

Дифференцируя это равенство как тождество, т.е. дифференци-

руя обе его части, находим

y′= (x ln x)′=

ln x + 1.

Следовательно,

′

(1+ ln x)

y =

Пример 2.

Найти производную функции y = (sin x)cosx,

x (0, π ).

Решение.

Логарифмируя,

получаем: ln y = cos x ln sin x,

y′

(cosx lnsinx)

′

sinx lnsinx +

cosx

y =

= −

cosx sinx

Отсюда имеем,

что

′

sin x

cos x − 1

(cos

x − sin

x ln sin x) .

20.

Производная

неявной

функции.

Пусть

функция

y = y (x)

задана неявно:

F (x, y) = 0.

(3)

Для нахождения производной y′будем дифференцировать обе части равенства (3), считая, что х – независимая переменная, а у есть функция переменной х. Из полученного уравнения найдем y′. Проиллюстрируем этот метод на следующем примере.

Пример 3. Найти производную функции у, заданной уравнением

y = cos (x + 3y).

(4)

Решение. Дифференцируем обе части уравнения (4): y′= − sin(x + 3y)( x + 3y) ′,

y′= − sin(x + 3y)(1+ 3y)′.

Решаем полученное уравнение относительно y′:


′		(x +		′	− sin( x + 3y) ,
y +	3sin			3y)y =
	y′=		−	sin (x +	3y)
						.
			1+	3sin (x + 3y)

178

30. Производные высших порядков. Пусть функция f (x)

имеет производную в каждой точке x (a; b). Тогда на промежутке (а; b) будет определена функция f ′(x) , и тоже можно говорить о ее производной.

Назовем f ′(x) производной первого порядка функции f (x). Про-

изводной второго порядка функции f (x) называется производная от функции f ′(x) , если она существует. Обозначается вторая производная символами y′, f ′(x) .

Производную от второй производной называют производной третьего порядка функции f (x) и обозначают y′, f ′(x) .

Производная n-го порядка является производной от производной (n – 1)-го порядка. Производная n-го порядка обозначается y(n), f (n)(x).

Производные высших порядков широко применяются, в частности, в физике. Выясним, например, физический смысл второй производной.

Пусть материальная точка движется прямолинейно и пройденный ею путь описывается уравнением s = s (t), t – время. Как известно из Л.27, первая производная от пути по времени есть мгновенная скорость движения точки в момент времени t, v(t) = s′(t) . Тогда вторая производная от пути по времени s′(t) равна скорости изменения функции скорости v (t). А это есть ускорение а (t) материальной точки в момент времени t. Таким образом, вторая производная от пути по

времени есть ускорение,

т.е. a(t) =

′

s ( t) .

Теперь найдем производные n-го порядка для некоторых элемен-

тарных функций.

1) Найдем y(n) степенной функции y = xα , x

(0, +∞

), α

R. Очевидно,

y′= α x α − 1, y′= α (α − 1) x α − 2 ,$, y (n) = α (α − 1) $ (α − n + 1) x α − n .

Если предположить, что α

k N ,

то y (k )

(x k )(k ) =

k (k −

1)$2 ×1 = k!,

y (

k +

) = (k!)

= 0 .

′

2) Замечательным свойством обладает показательная функция

y = ex. Для любого n справедлива формула

(ex)(n) = ex.

(5)

Найдем n-производную функции y = sin x.

Будем иметь

′

cos x = sin x +

cos x +

sin x + 2

y =

, y =

179

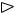
′			π				π	.
	cos x +	2		=	sin x +	3
y =			2				2

С помощью метода математической индукции можно показать, что

(sin x)	(n)					π
		=	sin	x +	n			.		(6)
		=	sin	x +	n	2		.		(6)
						2
Аналогично,
(cos x)	(n)						π
		=	cos	x +	n				.	(7)
		=	cos	x +	n				.	(7)
							2

Приведем еще одну формулу для нахождения производной n-го порядка. Пусть y = u v, где u и v – некоторые функции, имеющие производные любого порядка. Будем последовательно находить производные от функции у:

y ′= u′v + uv′, y ′= u′v + u′v′+ u′v′+ uv′= u′v + 2u′v′+ uv′,

y ′= u′v + u′v′+ 2u′v′+ 2u′v′+ u′v′+ uv′= u′v + 3u′v′+ 3u′v′+ uv′.

Правые части полученных формул похожи на разложение степеней бинома Ньютона (u + v)n, n = 1, 2, 3. Только вместо показателей степени стоят порядки производных. Сами функции u и v следует рассматривать в этом случае как производные нулевого порядка u = u(0), v = v(0).

Тогда можно записать формулу для производной n-го порядка:

y (n) =

(uv)(n) = u(n)v( 0) + nu( n− 1) v′+

n(n − 1)

u(n− 2)v′+ $+

(8)

n(n − k)$( n

− k + 1)

(n− k )

( k)

+ $+

( 0)

( )n

Эта формула называется формулой Лейбница. Ее можно доказать методом математической индукции.

Пример 4. Найти n-ую производную функции y = x2sin x.

Решение. Полагаем u =sin x, v = x2 и применим формулу Лейбница. Найдем

(n)

′

′ ′

(n)

sin x + n

;

0, n = 3, 4,

Подставляя в формулу (8), имеем

180

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 4118 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.11.2018253.44 Кб9второй курсач(разработка)(Кристина)2.doc
#
13.09.201940.04 Кб6Вуліца Замкавая.docx
#
18.02.2016147.97 Кб2вучэбная праграма 2012.doc
#
19.02.201612.77 Mб65Высшая матем. Учебник.pdf
#
22.09.2019956.93 Кб18Высшая математика (1).doc
#
18.02.20165.88 Mб72высшая математика.pdf
#
18.02.2016192.33 Кб16Вычеты аналитических функций..pdf
#
18.02.2016190.98 Кб4гістарычная навука Бел. раб. праграма 2012.doc
#
14.04.2019380.93 Кб13Гісторыя Беларус(шпоры).doc
#
12.11.2019311.93 Кб3Гісторыя беларускага сялянства. Т.2..docx
#
15.04.2019130.2 Кб4гістрыя вся.docx