высшая математика

Точки А и В лежат в одной плоскости, перпендикулярной оси вращения Ox.

Тогда X = x, Y 2 + Z 2 = y2. Подставляя выражения для х и у в уравнение данной прямой, получим уравнение искомой поверхности вращения:

Таким образом, поверхностью вращения является конус с вершиной в точке M (4; 0; 0).

30. Общее уравнение поверхности второго порядка.

Общее уравнение второй степени относительно x, y, z имеет вид

Это уравнение может определять сферу, эллипсоид, однополостный или двуполостный гиперболоид, эллиптический или гиперболический параболоид, цилиндрическую или коническую поверхность второго порядка. Оно может также определять совокупность двух плоскостей, точку, прямую или даже не иметь геометрического смысла, т.е. определять «мнимую» поверхность.

Если D = E = F = 0, т.е. квадратичная форма (11) имеет канонический вид, общее уравнение (10) принимает форму:

Вэтом случае уравнение легко упрощается с помощью параллельного переноса осей координат, что позволяет сразу установить его геометрический смысл.

Вобщем случае нужно вначале применить линейное преобразование, приводящее квадратичную форму (11) к каноническому виду, как это сделано в Л.16, и получить уравнение второй степени относи-

тельно новых переменных x′, y′, x′в виде (12).

111

Пример 2. Каков геометрический смысл уравнения x2 + y2 + z2 – yz – xz – xy = 0?

Решение. Умножим на 2 и перепишем уравнение в виде

2x2 + 2y2 + 2z2 – 2yz – 2xz – 2xy = 0 или (x – y)2 + (y – z)2 + (x – z)2 = 0.

Этому уравнению удовлетворяют координаты только тех точек, для которых выполняются равенства x = y, y = z, x = z.

Таким образом, уравнение определяет прямую x = y = z.

Пример 3. Привести к каноническому виду уравнение x2 – y2 – 4x + 8y – 2z = 0.

Решение. Сгруппируем члены, содержащие х и у: (x2 – 4x) –

– (y2 – 8y) = 2z. Дополним до полных квадратов выражения в скоб-

ках и получим: (x2 – 4x + 4) – (y2 – 8y + 16) = 2z + 4 – 16 или (x – 2)2 –

– (y – 4)2 = 2(z – 6).

которое приводит квадратичную форму 6x2 + 3y2 + 3z2 + 4xy + 4xz –

112

Дополняя до полных квадратов выражения, содержащие x′и z′, получаем:

Итак, каноническое уравнение имеет вид (15) и представляет собой однополостный гиперболоид вращения вокруг оси Ox′кривой

(y′)2 − (x′)2 = 1, z′= 0 .

124 62

441 63

! Задания для самостоятельной работы

1. Выяснить, какие поверхности определяются следующими уравнениями:

a) x2 + 2y2 + 2z2 – 4y + 4z + 4 = 0; б) x2 + y2 – z2 – 2х – 2y + 2z + 2 = 0; в) 5x2 – z2 – 18х – 18y – 6z + 4 = 0;

г) 3x2 + 3y2 – 12х + 12y – 2z + 4 = 0.

2. Привести к каноническому виду уравнения:

а) 4x2 + 9y2 + 36z2 – 8x – 18y – 72z + 13 = 0; б) 2x2 + 7y2 + zy – 3x + 2 = 0;

в) x2 + z2 – 5xy + 3z – 2y + 3 = 0.

3. Каков геометрический смысл уравнения

x2 + 4y2 + 9z2 + 12yz + 6xz + 4xy – 4x – 8y – 12z + 3 = 0?

113

Лекция 20

Системы линейных неравенств

Приводится решение линейных неравенств в пространстве R2, исследуются смешанные системы линейных уравнений и неравенств, рассмотрены эквивалентные преобразования систем линейных уравнений и неравенств.

10. Решение линейных неравенств в R 2. Рассмотрим некоторое неравенство относительно переменных x1, x2,..., xn :

Переменные x1, x2,..., xn будем толковать как координаты точки или вектора n-мерного пространства R n.

Совокупность точек пространства R n, координаты которых удовлетворяют неравенству (1), назовем областью решений неравенства (1) . Эта область является полупространством.

Область решений системы линейных неравенств

представляет собой пересечение некоторого числа полупространств. Полупространство – это выпуклое множество, т.е. такое множество точек n-мерного пространства, которое наряду с любыми своими двумя точками содержит и весь отрезок, их соединяющий. Выпуклым будет и пересечение выпуклых множеств, отсюда вытекает, что областью решений системы (2) будет выпуклый многогранник (или выпуклая неограниченная многогранная область), ограниченный гиперплоскостями, уравнения которых получаются из неравенств системы (2) заменой в них знаков неравенств на знаки равенств. Многогранник представляет собой пересечение полупространств, ограниченных

этими гиперплоскостями.

В случае n = 2 (двумерного пространства) неравенство (1) принимает вид:

114

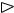
В другой полуплоскости выполняется противоположное неравен-

будет выпуклый многоугольник или выпуклая многоугольная область, ограниченная прямыми, уравнения которых получаются из неравенств системы заменой в них знаков неравенства на знаки равенств. Указанный многоугольник или многоугольная область есть пересечение полуплоскостей, ограниченных этими прямыми.

Пример 1. Найти область решений системы неравенств:

2x1 − 5x2 ≥ − 10,

x1 ≤ 5,

3x1 + 2x2 ≥ 6,

x1 + 2x2 ≥ − 2.

неравенствам (рис. 1). Стрелки указывают полуплоскости, являющиеся областями решений данных неравенств.

Пересечение отмеченных полуплоскостей – четырехугольник АВСD – и есть область решений данной системы.

20. Смешанные системы линейных уравнений и не-

равенств. В приложениях, в частности, при решении задач линейного программирования нужно уметь находить решение систем линейных неравенств или смешанных систем, состоящих из линейных уравнений и неравенств с большим числом неизвестных. Построить графическое изображение множества решений в этих случаях затруднительно. Но задачу можно свести к решению эквивалентной системы, содержащей только линейные уравнения, а такие системы решить, например, методом Гаусса. Основанием указанного преобразования является следующее утверждение: любому решению x10, x20,..., xn0 неравенства

115

Решение. Используя сформулированное выше правило перехода к эквивалентной системе линейных уравнений, введем неизвестные x6, x7, получим следующую систему, эквивалентную данной:

Для полученной системы уравнений составим расширенную матрицу:

116

Используя алгоритм полного исключения, выделяем диагональную подматрицу, выбирая разрешающие элементы так, как это делается при поиске опорных решений. Примем за разрешающий, например, пятый столбец. Разрешающую строку находим из условия

Ею будет первая строка, а разрешающим – элемент 1. Выполним первое исключение и получим матрицу:

Второе исключение выполним, например, со вторым столбцом.

переставляя в которой пятый, шестой и второй столбцы, соответствующие базисным переменным x2, x5, x6, можно образовать диагональную подматрицу. Решение закончено, т.к. на основании последней матрицы x1 = x3 = x4 = x7 = 0 сразу определяются значения базисных

117

30. Эквивалентные преобразования систем линей-

ных уравнений и неравенств. Переход от системы линейных уравнений к эквивалентной системе неравенств осуществляется на основе следующего утверждения, обратного утверждению, сформули-

с условиями неотрицательности переменных xj ≥ 0, ϕ = 1,2,3,4 к эквивалентной системе неравенств.

Решение. Составим для системы (5) расширенную матрицу, преобразуем ее по алгоритму полного исключения до выделения единичной подматрицы:

Присоединяя к полученным неравенствам неиспользованное условие неотрицательности для переменных х2 и х4, получим систему неравенств:

118

эквивалентную системе уравнений (5).

! Задания для самостоятельной работы

1. Построить область решений следующих систем неравенств:

2. Найти какое-нибудь опорное решение смешанной системы линейных уравнений и неравенств:

x1 − 2x2 + x4 = − 3,

x3 − 2x4 = 2,3x2 − x4 + x5 ≤ 5,

x2 + x5 ≥ − 3.

3. Преобразовать следующие системы линейных уравнений в эквивалентные системы линейных неравенств:

119

Часть II

ВВЕДЕНИЕ В АНАЛИЗ. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

Лекция 21

Числовые последовательности. Предел числовой последовательности

Вводятся понятия числовой последовательности. Рассматриваются бесконечно малые и бесконечно большие последовательности и свойства сходящихся последовательностей.

10. Числовая последовательность. Пусть N – множе-

ство натуральных чисел. Если каждому натуральному числу n

называют элементами, или членами последовательности. Числовую последовательность (в дальнейшем – последовательность) будем еще записывать в виде xn , а выражение xn называть общим членом последовательности, n – номером члена.

Последовательности встречались в средней школе, например, бесконечная геометрическая прогрессия 1, q, q2,..., qn,..., q < 1 является числовой последовательностью.

определений и теорем используются слова «существует» и «для любого». Для краткости записи вместо этих терминов будем использовать символы соответственно и . Символ называют квантором существования, а символ – квантором общности.

С помощью указанных символов определение ограниченной последовательности выглядит следующим образом: последова-

120