
высшая математика
.pdf
 Лекция 4
Лекция 4
Прямая на плоскости
Рассмотрены различные виды уравнений прямой на плоскости.
10. Уравнение прямой с угловым коэффициентом.
Рассмотрим некоторую прямую, не перпендикулярную оси Ох. Назовем углом наклона данной прямой к оси Ох угол α , на который нужно повернуть ось Ох, чтобы положительное направление совпало с одним из направлений прямой. Тангенс угла наклона прямой к оси Ох называют угловым коэффициентом этой прямой и обозначают буквой k:
k = tg α . |
(1) |
|||
Из формулы (1), в частности, следует, что если α = 0, т.е. прямая па- |
||||
раллельна оси Ox, то k = 0. Если |
α = |
π |
, т.е. прямая перпендикуляр- |
|
2 |
||||
на оси Ox, то выражение k = tg α |
|
|
||
не имеет смысла. Тогда говорят, что |
||||
угловой коэффициент «обращается в бесконечность» (рис. 1). |
||||
Выведем уравнение прямой, если известны ее угловой коэффи- |
||||
|
|
|
циент и величина отрезка ОВ, |
|
|
|
|
которую она отсекает на оси |
|
|
|
|
Oy. |
|
|
|
|
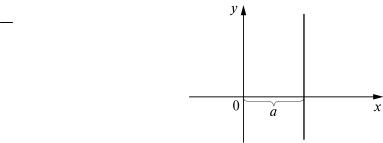
Пусть М – произвольная |
|
|
|
|
точка плоскости с координата- |
|
|
|
|
ми х и y. Если провести пря- |
|
|
|
|
мые BN и NM, параллельные |
|
|
|
|
осям, то образуется прямо- |
|
|
|
|
угольный треугольник. Точка |
|
|
|
|
М лежит на прямой тогда и |
|
Рис. 1 |
|
|
только тогда, когда величины |
|
|
|
BN и NM удовлетворяют ус- |
||
|
|
|
||
ловию NMBN = tg α . Но NM = CM – CN = CM – OB = y – b, BN = x. Отсю-
да, с учетом формулы (1), получаем, что точка M лежит на данной прямой тогда и только тогда, когда ее координаты удовлетворяют урав-
нению |
y − b |
= |
k , которое после преобразования примет вид: |
|
x |
|
|||
|
|
у = kx + b. |
(2) |
|
|
|
|
2 1

Уравнение (2) называют уравнением прямой с угловым коэффи-
циентом. Если k = 0, то прямая параллельна оси Ox, и ее уравнение имеет вид y = b.
Итак, любая прямая, не перпендикулярная оси Ox, имеет уравнение вида (2). Верно и обратное: любое уравнение вида (2) определяет прямую, которая имеет угловой коэффициент k и отсекает на оси Oy отрезок, величина которого b.
Пример 1. Составить уравнение прямой, отсекающей на оси Oy |
|||||||
отрезок b = 2 и образующей с осью Ox угол α = |
|
π |
. |
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
||
Решение. Находим угловой коэффициент: |
k = tg α = |
|
π |
|
= 3 . |
||
tg |
3 |
|
|||||
|
|
|
|
|
|
|
|
Подставляя k и b в уравнение (2), получаем искомое уравнение прямой:
y =  3x + 2 или y −
3x + 2 или y −  3x − 2 = 0 .
3x − 2 = 0 . 
20. Уравнение прямой, проходящей через данную точку, с данным угловым коэффициентом. Иногда возни-
кает необходимость составить уравнение прямой, зная одну ее точку M1(x1; y1) и угловой коэффициент k. Запишем уравнение прямой в виде (2), где b, пока неизвестное число. Так как прямая проходит через точку
M1(x1; y1), то координаты этой точки удовлетворяют уравнению (2): |
||||||
y1 |
= kx1 + b. Отсюда b = y1 – kx1. |
|
|
|
||
|
Подставляя это в уравнение (2), получаем искомое уравнение |
|||||
прямой: |
|
|
|
|||
|
y – y1 = k (x – x1). |
(3) |
||||
|
Пример 2. Составить уравнение прямой, проходящей через точку |
|||||
М (1;2) и образующей с осью Ox угол α = |
π |
. |
|
|
|
|
|
|
|
|
|||
|
4 |
|
|
π |
|
|
|
Решение. Находим угловой коэффициент: |
k = tg α = tg |
= 1. |
|||
|
|
|||||
|
|
|
|
4 |
|
|
Подставляя данные координаты и значение углового коэффициента k в уравнение (3), получим искомое уравнение прямой:
y – 2 = x – 1 или y – x – 1 = 0. 
30. Уравнение прямой, проходящей через две дан-
ные точки. Пусть даны две точки M1(x1; y1) и M2(x2; y2). Приняв в (3) точку М (х; y) за M2(x2; y2), получим: y2 – y1 = k (x2 – x1).
2 2

Если x2 ≠ x1 , то, определяя k из последнего равенства и подставляя его в уравнение (3), получаем искомое уравнение прямой:
y − y = |
y2 − |
y1 |
(x − x ) |
. |
|
|
|||
1 |
x2 − |
1 |
||
|
x1 |
|
||
Это уравнение, если y2 ≠ y1 , можно записать в виде:
y − |
y1 |
= |
x − |
x1 |
. |
(4) |
||||
y |
|
− |
y |
x |
|
− |
|
|||
2 |
|
2 |
x |
|
||||||
|
|
1 |
|
|
|
1 |
|
|
||
Если y1 = y2, то уравнение искомой прямой имеет вид y = y1, и такая прямая параллельна оси Ox. Если x1 = x2, то прямая, проходящая через точки M1 и M2, параллельна оси Oy, ее уравнение имеет вид x = x1.
40. Общее уравнение прямой.
Теорема 1.
В прямоугольной системе координат любая прямая задается уравнением первой степени
Ax + By + C = 0, |
(5) |
и, обратно, уравнение (5) при произвольных коэффициентах А, В, С (А и В одновременно не равны нулю) определяет некоторую прямую в прямоугольной системе координат Oxy.
Доказательство. Докажем вначале первое утверждение. Если прямая не перпендикулярна оси Ox, то, как было показано в п. 1, она определяется уравнением первой степени: y = kx + b, т.е. уравнением вида (5), где A = k, B = –1 и C = b. Если прямая перпендикулярна оси Ox, то все ее точки имеют одинаковые абсциссы, равные величине а отрезка, отсекаемого прямой на оси Ox (рис. 2).
Уравнение такой прямой имеет вид x = a, т.е. также вида (5), где A = 1, B = 0, C = –a. Первое утверждение доказано.
Докажем обратное утверждение. Пусть дано уравнение (5), где хотя бы один из коэффициентов А или В не равен нулю.
Если B ≠ 0, то (5) можно записать в виде: y = − BA x − CB .
Полагая k = − BA , b = − CB , получаем уравнение y = kx + b, т.е. уравнение вида (2), которое определяет прямую.
Если B = 0, то A ≠ 0, и (5) принимает вид x = − CA . Обозначая
2 3
a = − CA , получаем x = a, т.е.
уравнение прямой, перпендикулярной оси Ox. 
Линии вида (5) называются линиями первого порядка. Уравнение вида Ax + By + C = 0 называется общим уравнением прямой, или полным уравнением прямой. При различных значениях А, В, С
оно определяет всевозможные Рис. 2 прямые.
50. Неполные уравнения первой степени. Уравне-
ние прямой «в отрезках». Рассмотрим три частных случая, когда уравнение Ax + By + C = 0 является неполным, т.е. один из коэффициентов равен нулю.
1) C = 0; уравнение имеет вид Ax + By = 0 и определяет прямую, проходящую через начало координат;
2) B = 0 (A ≠ 0); уравнение имеет вид Ax + C = 0 и определяет прямую, параллельную оси Oy. В частности, уравнение x = 0 определяет ось ординат;
3) A = 0 (B ≠ 0); уравнение имеет вид By + C = 0 и определяет прямую, параллельную оси Ox. В частности, уравнение y = 0 определяет ось абсцисс.
Рассмотрим теперь уравнение Ax + By + C = 0 при условии, что ни один из коэффициентов А, В, С не равен нулю. Преобразуем его к виду:
|
x |
+ |
|
y |
= 1. |
|
|
|
|
|
|
|
|
|
− |
C |
− |
C |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
A |
|
|
B |
|
|
C |
|
|
|
|
C |
|
|
|
|
Вводя обозначения a = − |
|
, |
b = |
− |
, получаем |
|||||||
|
|
|
|
A |
B |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x |
+ |
|
y |
= |
1. |
|
(6) |
|
|
|
|
|
|
|
a |
|
b |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнение (6) называется уравнением прямой «в отрезках». Числа
а и b являются величинами отрезков, которые прямая отсекает на осях координат. Эта форма уравнения удобна для геометрического построения прямой.
2 4

Пример 3. |
Прямая задана уравнением 2х – 3у + 6 = 0. Составить |
||||||
для этой прямой уравнение «в отрезках» и построить прямую. |
|||||||
Решение. Для данной пря- |
|
||||||
мой уравнение «в отрезках» |
|
||||||
имеет вид: |
|
x |
+ |
|
y |
= 1 . |
|
− |
3 |
2 |
|
||||
|
|
|
|
||||
Чтобы построить эту пря- |
|
||||||
мую, отложим на осях коорди- |
|
||||||
нат Ох и Оу отрезки, величины |
|
||||||
которых соответственно равны |
|
||||||
а = –3, b = 2, и проведем прямую |
|
||||||
через точки M1(–3; 0) и M2(0; 2) |
Рис. 3 |
||||||
(рис. 3). |
|
|
|
|
|
|
|
! Задания для самостоятельной работы
1. Составить уравнение прямой, отсекающей на оси Oy отрезок
b = 4 и образующей с осью Ox угол α = π4 .
2. Построить прямую, заданную уравнением
y = 34 x + 2 .
3. Составить уравнение прямой, проходящей через точку
М (2; 1) и образующей с осью Ox угол α = π6 .
4. Составить уравнение прямой, проходящей через точки M1(3; 1)
и M2(5; 4).
5. Дано общее уравнение прямой 12x – 5y – 65 = 0. Написать уравнение прямой с угловым коэффициентом.
6. Прямая задана уравнением 3x – 5y + 15 = 0. Составить для этой прямой уравнение «в отрезках» и построить прямую.
7. Установить, какую линию описывает середина отрезка между двумя пешеходами, идущими по двум взаимно перпендикулярным дорогам с одинаковой скоростью.
2 5
 Лекция 5
Лекция 5
Расположение двух прямых на плоскости
Приведены формулы тангенса угла между двумя прямыми и расстояния от точки до прямой, условия параллельности и перпендикулярности двух прямых, рассмотрено взаимное расположение двух прямых на плоскости.
10. Угол между двумя прямыми. |
|
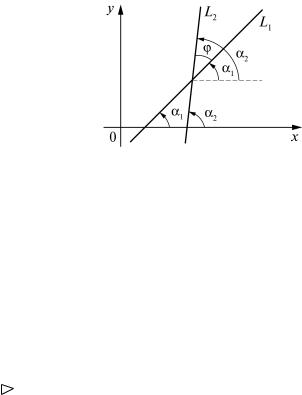
Рассмотрим две прямые L1 и L2. Пусть уравнение L1 имеет вид |
|
y = k1x + b1, |
где k1 = tg α 1, а уравнение L2 – вид y = k2x + b2 , где |
k2 = tg α 2, а ϕ |
– угол между прямыми L1 и L2, 0 ≤ ϕ < π (рис. 1). |
Рис. 1
Из геометрических соображений (рис. 1) устанавливаем соотно-
шение между углами α 1, α 2, ϕ |
: α |
2 = α |
1 + ϕ или ϕ = α 2 – α |
1 , откуда |
||||||||
|
tgϕ |
= tg(α 2 − α |
1) = |
|
tgα |
2 − |
tgα 1 |
, или |
|
|||
|
1+ |
tgα |
|
|
||||||||
|
|
|
|
|
1tgα 2 |
|
||||||
|
|
tgϕ = |
k2 − |
k1 |
. |
|
(1) |
|||||
|
|
1 |
+ k k |
2 |
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Формула (1) определяет один из углов между прямыми. Второй |
||||||||||||
угол равен π |
– ϕ . |
|
|
|
|
|
|
|
|
|
|
|
Пример |
1. |
Прямые |
заданы |
|
уравнениями |
у = 3х + 2 и |
||||||
у = –2х + 3. Найти угол между этими прямыми.
2 6

Решение. Имеем k1 = 3, k2 = –2. Поэтому по формуле (1) нахо-
дим |
tg ϕ = |
− 2 − 3 |
|
= |
− 5 |
= 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1+ (− 2) 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
− 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Таким образом, |
один из углов между данными прямыми равен |
π |
, |
|||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||
другой угол π − |
π |
= |
3π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
20. Условие параллельности и перпендикулярности |
||||||||||||||||||||||||
двух прямых. Если прямые L1 |
и L2 |
параллельны, то ϕ = 0 и tg ϕ = 0. В |
|||||||||||||||||||||||
этом случае числитель правой части формулы (1) равен нулю, т.е. k2 – |
|||||||||||||||||||||||||
k1 = 0, откуда k1 = k2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Таким образом, условием параллельности двух прямых является |
||||||||||||||||||||||||
равенство их угловых коэффициентов. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Если прямые L и L перпендикулярны, т.е. ϕ |
= |
|
π |
|
, то из (1) находим |
|||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ctg ϕ |
= |
1+ k1k2 |
. В этом случае |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
k2 − |
k1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ctg |
π |
= |
0 и 1+ k k |
2 |
= 0 |
, откуда k |
2 |
= |
− |
1 |
. |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2 |
|
|
|
1 |
|
|
|
|
k1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Таким образом, условие перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку.
Пример 2. Показать, что прямые 2х – 3у |
+ |
|
1 = 0 и |
||||||||||||||
6х – 9у + 2 = 0 параллельны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Приведя каждое из уравнений прямой к виду уравне- |
|||||||||||||||||
ния с угловым коэффициентом, получаем y = |
2 |
x + |
1 |
|
|
и |
y = |
|
2 |
x + |
|
2 |
. |
||||
3 |
|
3 |
|
|
|
|
|
|
3 |
|
|
9 |
|
||||
Угловые коэффициенты этих прямых равны |
k |
1 |
= |
k |
2 |
= |
|
2 |
. |
Значит, |
|||||||
3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
прямые параллельны. 
2 7

30. Расстояние от точки до прямой.
Теорема 1.
Расстояние d от данной точки М(х0; у0) до прямой L, заданной уравнением Ax + By + C = 0, на плоскости определяется формулой:
d = |
Ax0 + |
By0 + |
C |
. |
(2) |
A2 + B2 |
|
||||
|
|
|
|
||
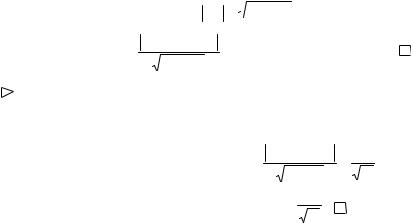
Рис. 2
Доказательство. Рассмотрим на прямой L две произвольные точки E и F с координатами (x1; y1) и (x2; y2). Вычислим длину отрезка
EF и площадь SMEF треугольника MEF (рис. 2).
Для этого запишем уравнение прямой по формуле (Л.4.4):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y − |
y1 |
|
= |
|
|
x − |
|
|
|
x1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
− |
y |
|
|
x |
2 |
− |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
откуда |
|
|
|
(y − |
|
y1)( x2 − |
|
|
x1) |
−( |
x − |
x)(1 |
|
|
y2 − |
y)1 |
= 0 . |
|
|
|
|
(3) |
||||||||||||||||||||||
Площадь SMEF запишем по формуле (Л.2.3): |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2S |
MEF |
= |
|
(x |
2 |
− |
x )( |
y |
0 |
− |
|
|
y) |
−( |
x |
0 |
− |
x)( y |
2 |
− |
y) |
|
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
||||||||||||
Далее |
|
EF |
|
= |
|
|
|
(x |
2 |
− |
x )2 |
|
+ |
( |
y |
2 |
− |
|
|
y) |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
2 |
− |
x )( |
y |
0 |
− |
y) |
−( x |
0 |
− |
|
x)( |
y |
2 |
− y) |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
d = |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
. |
|
(4) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(x |
2 |
− |
x )2 + |
( |
y |
2 |
− |
y ) 2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
С помощью уравнения (3) выразим коэффициенты А, В, С уравне-
2 8
ния Ax + By + C = 0 прямой L через координаты точек Е и F. Для этого перепишем уравнение (3) в виде:
(y1 − y2 )x + ( x2 − x1) y + x1( y2 − y)1 − y(1 x2 − x)1 = 0 ,
откуда получаем A = y1 – y2, B = x2 – x1, C = x1 (y2 – y1) – y1 (x2 – x1).
Тогда 2SMEF = | Ax0 + By0 + C|; EF =  A2 + B2 , и формулу (4) мож-
A2 + B2 , и формулу (4) мож-
но записать в виде d = |
Ax0 |
+ By0 + C |
, что и требовалось доказать. |
|||||
|
A2 + B2 |
|||||||
|
|
|
|
|
|
|
|
|
Пример 3. Пусть |
прямая |
L |
задана |
уравнением |
||||
2х – 3у + 5 = 0 и дана точка М (1; 2). Найти расстояние d |
от точки М |
|||||||
до прямой L. |
|
|
|
|
|
|
|
|
Решение. По формуле (2) имеем |
d = |
2 1− |
3 2 + |
5 = |
1 . |
|||
|
|
|
|
|
22 + 32 |
|
13 |
|
|
|
|
|
|
|
1 |
|
|
Таким образом, искомое расстояние равно |
13 . |
|
||||||
40. Взаимное расположение двух прямых на плос- |
||||||||
кости. Пусть прямые L1 и L2 заданы уравнениями: |
|
|
||||||
A1x + |
B1y + C1 = 0 (L1) |
|
|
(5) |
||||
|
|
B2 y + C2 = 0. (L2 ) |
|
|
||||
A2 x + |
|
|
|
|||||
Рассмотрим эти уравнения как систему двух уравнений с двумя неизвестными х и y. Решая эту систему, находим:
|
x = |
|
B1C2 − B2C1 |
, y |
= |
A2C1 − A1C2 |
. |
||||||||
|
|
|
|||||||||||||
|
|
|
A B − |
A B |
|
A B |
2 |
− |
A B |
||||||
|
|
1 |
2 |
2 |
1 |
|
1 |
|
|
2 |
1 |
|
|||
Пусть А1В2 – А2В1 |
≠ |
0. Полученные формулы дают решение систе- |
|||||||||||||
мы (5). Это значит, что прямые L1 и L2 непараллельны и пересекаются в |
|||||||||||||||
одной точке с координатами (х; y). |
|
|
|
|
|
|
|
|
|||||||
Пусть теперь А1В2 |
– А2В1 |
= 0. Возможны два случая: |
|||||||||||||
1) А2С1 |
– А1С2 |
= 0 и В1С2 – В2С1 |
= 0; |
|
|
|
|
|
|
||||||
2) А2С1 |
– А1С2 |
≠ 0 (В1С2 – В2С1 ≠ 0). |
В2 = mВ1, С2 = mС1 , |
||||||||||||
В первом случае имеем А2 = mА1, |
|||||||||||||||
2 9
или |
A2 |
= |
B2 |
= |
C2 |
= |
m , |
|
A |
B |
C |
||||||
|
|
|
|
|
||||
|
1 |
|
1 |
|
1 |
|
|
где m ≠ 0 – некоторое число. Это означает, что коэффициенты уравнений пропорциональны, откуда следует, что второе уравнение получается из первого умножением на число m. В этом случае прямые L1 и L2 со-
впадают, т.е. их уравнения определяют одну и ту же прямую. Оче-
видно, что система (5) имеет бесконечно много решений.
Во втором случае, если, например, А2С1 – А1С2 ≠ 0 , то, допустив, что система (5) имеет некоторое решение (х0; у0), получим противоречие. Действительно, подставляя в уравнения вместо х и y значения х0 и у0, умножая первое уравнение на А2, второе – на А1 и вычитая из первого уравнения второе, получим А2С1 – А1С2 = 0, что противоречит предположению. Таким образом, система (5) решения не имеет. В этом случае прямые L1 и L2 не имеют точек пересечения, т.е. они параллельны.
Итак, две прямые на плоскости либо пересекаются в одной точке, либо совпадают, либо параллельны.
!Задания для самостоятельной работы
1.Две прямые заданы уравнениями у = х – 0,5 и у = 2х + 1. Найти угол между этими прямыми.
2.Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 5 = 0 перпендикулярны.
3.Показать, что прямые х + у – 1 = 0 и 2х + 2у – 3 = 0 парал-
лельны.
4.Пусть прямая L задана уравнением х – 5у + 11 = 0 и дана точ-
ка М (5; 2). Найти расстояние d от точки М до прямой L.
5. Найти уравнение прямой, проходящей через точку пересечения прямых 2х – 3у – 1 = 0 и 3х – y – 2 = 0 и перпендикулярной прямой
у = х + 1.
3 0
