Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

высшая математика

.pdf

Скачиваний:

Добавлен:

18.02.2016

Размер:

5.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 414 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Лекция 6

Векторы

Дается понятие вектора, рассмотрены линейные операции над векторами, скалярное произведение векторов.

10. Дадим вначале геометрическое толкование вектора, используя понятие направленного отрезка, данное в лекции 2. Напомним, что направленным отрезком называют отрезок определенной длины и определенного направления. Направленный отрезок с фиксированным началом

А и концом В называется связанным вектором и обозначается AB . Если для направленного отрезка фиксируются только его длина и направле-

		!			!	!
ние, то он называется свободным вектором (обозначение a ,					b ,	x ...).
Длиной связанного вектора AB (модулем, нормой) называется рас-
стояние между точками А, В и обозначается	AB	; запись	!	также озна-

			a
чает длину (связанного или свободного) вектора		!
		a , которую находят как

длину соответствующего направленного отрезка.

Вектор, начало и конец которого совпадают, называется нулевым и обо-

!	(он имеет произвольное направление и для него					!	= 0 ).
значается 0	(он имеет произвольное направление и для него					0	= 0 ).
			!	!
			!	!
Говорят, что два ненулевых вектора a				, b есть коллинеарные, если
				!	!
они параллельны одной и той же прямой; два вектора a					, b называются
!	!
равными (a	= b), если они одинаково направлены и имеют равные модули.
Углом между векторами		!	!
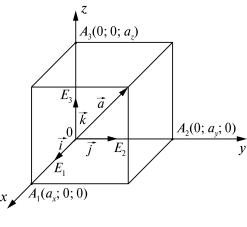
Углом между векторами		a	и b будем называть наименьший угол
			!
ϕ , на который нужно повернуть вектор a , чтобы его направление совпа-
дало с направлением вектора		!
дало с направлением вектора		b , при условии, что оба вектора отнесены

к общему началу (рис. 1).

Рис. 1

3 1

						! !
В этом случае вводится обозначение ϕ =							. Очевидно, что
В этом случае вводится обозначение ϕ =						a,b	. Очевидно, что
		! !		π
0 ≤ ϕ ≤ π . Если		a,b	=	π	, то векторы называются ортогональными
				2
!
(считаем, что 0	ортогонален любому вектору).

По аналогии с лекцией 2 рассмотрим декартову прямоугольную систему координат в пространстве. Для ее построения выберем точку О (начало системы координат) и проведем через эту точку взаимно перпендикулярные оси: Ox (ось абсцисс), Oy (ось ординат), Oz (ось апликат). На каждой оси отложим отрезки OE1, OE2, OE3 единичной длины. Полученные единичные отрезки рассмотрим как направленные, причем их направ-

ления совпадают соответственно с направлением осей Ox, Oy, Oz. Обозна-

чим i =

j =

k =

и назовем их ортами. Вектор i считаем

первым,

–

вторым,

– третьим вектором, и условимся, что тройка

векторов (i ,

k) имеет правую ориентацию.

Таким образом, в пространстве R3 построена декартова прямо-

угольная система координат, которую обозначим Oxyz (рис. 2).

в рассматриваемой системе коор-

Очевидно, что орты i ,

, k

динат

имеют

координаты:

i! = col (1; 0; 0) ,

!j = col

(0; 1; 0) ,

k = col (0; 0; 1) .

Произвольный вектор

можно разложить по ортам i

j ,

(рис. 2):

Рис. 2

3 2

!	= ax	!	+	!	+	!
a	= ax	j	+	ay j	+	az k ,
при этом координаты вектора			!	есть проекции этого вектора на оси
при этом координаты вектора			a	есть проекции этого вектора на оси

координат. Имеет место и обратное: для данной тройки действительных

чисел a , a	, a	z	можно построить единственный вектор пространства R3
x y		z		сначала строят соответствующие геометрические про-
(для чисел a , a , a				сначала строят соответствующие геометрические про-
	x		y z		!
екции, а затем сам вектор					a – как диагональ параллелепипеда). Таким

образом, с помощью декартовой системы координат Oxyz можно задать взаимно однозначное соответствие множества векторов пространства R3 и множества упорядоченных троек чисел.

Аналогично, в общем случае упорядоченную совокупность

col

(a ;a

;...; a

)

n вещественных чисел называют n-мерным век-

а числа

ai ,

i =

1, n

– координатами вектора

тором (обозначение a ),

a .

Правило

сложения

двух векторов:

col (a1

;a2 ;...; an )

a =

col

(b1;b2 ;...;bn )

;

col (a1 +

b1;a2 +

b2 ;...;an +

bn ) .

b =

a +

Правило вычитания:

= col (a1 −

b1;a2 −

b2 ;...; an −

bn ) .

a −

Правило умножения на число:

col (α

a1;α

a2 ;...; α

an ) .

Два вектора

тогда и только тогда, когда

равны ( a

= b )

равны их соответствующие координаты (ai=bi,

i =

1, n

Линейной комбинацией m векторов a

1, a2 ,......a m называется век-

тор

...+

, λ

, . . ., λ

a =

a1 +

am , где хотя бы одно из чисел λ

отлично от нуля.

Ненулевые векторы

b коллинеарны тогда и только тогда,

когда

(λ

≠

0) , что через координаты записывается так:

= λ a

= ... =

20.

Скалярное

произведение

векторов.

Скалярным

произведением двух векторов

называется число, равное произ-

и b

ведению длин этих векторов на косинус угла между ними:

3 3

! !

def

! !

(a, b) =

a b

cos

a, b .

Проекция вектора

на ось

определяется по формуле:

! !

npe!a

cos

a,e .

Из формул (1) и (2) имеем:

(a,b) =

npa!b

npb! a .

(1)

(2)

(3)

Для скалярного произведения векторов имеют место следующие свойства:

–

коммутативность;

(a,b) =

(b, a)

(α

! !

– ассоциативность;

a,b) =

α (a,b), α

! !

– дистрибутивность;

+ b,c) =

(a,c) +

(b,c)

> 0,

≠

! !

(a, a) =

0 ; (a, a) = 0

a = 0 .

Здесь R – множество действительных чисел.

Докажем, например, свойство 3). Используя формулу (3), свойство проекции и коммутативность скалярного произведения, получаем

! !

b, c) =

npc! (a

b) =

(npc!a

npc!b) =

npc!a

npc!b

= (! !) + (! !) , что и доказывает свойство 3). a,c b,c

С помощью понятия скалярного произведения можно сформулировать необходимое и достаточное условие ортогональности двух векторов: два ненулевых вектора являются ортогональными тогда и только тогда, когда их скалярное произведение равно нулю.

Из равенства (1) получаем формулу для вычисления косинуса угла между ненулевыми векторами:

	! !		!	!
	! !		(a,b)
		=	(a,b)

cos	a,b		!		!	.	(4)
			a		b

Из соотношений (3) можно получить также формулы для вычисления проекции одного вектора на второй с помощью скалярного произведения:

3 4

npa!b =

(a,b)				!
!		!
	!		,	np#a	=
	a			b
	a

!		!
(a,!b)			.	(5)
	b			(5)
	b

Следующая теорема отвечает на вопрос о представлении скалярного произведения в координатной форме.

Теорема 1.

Скалярное

произведение

двух

векторов

col (a1;a2 ;...; an ) и

a =

b =

col (b1;b2 ;...;bn )

равно сумме произведений соответствующих

координат:

a1b1 + a2b2 + ...anbn .

(6)

(a,b) =

Доказательство проведем для n

= 3. Рассмотрим декартову сис-

тему координат

Oxyz, и пусть

– соответствующие орты. Оче-

, j, k

видно, что

! !

= (

(i ,i )

j, j)

= (k , k) = 1 ,

(7)

! !

(i , j)

= (i , k)

= ( j, k) = 0 .

Рассмотрим скалярное произведение векторов a и

b, записав

их в форме разложения по ортам

! !

i , j, k , и используем свойства ска-

лярного произведения и равенства (7):

! !

(a,b)=

(axi +

ay j +

azk,bxi + by

j +

bzk )= axbx (i ,i)+

! !

+ axby (i

, j)+ axbz (i , k)+

aybx (j

, i ) + ay by(

j) +

+ ay bz (j, k)+ azbx(k

,i) +

azby( k

, )j + azb(z

k ,)k =

= axbx + ayby + azbz ,

что и требовалось доказать.

Пример 1. Установить связь между направляющими косинусами вектора в пространстве R3.

(

)

Имеем:

a =

cosα +

j cosβ +

a+1i

a+2 j

a3k .

cosγ =

cos

cos β = a2

cos γ= a3 .

a1, a

3 5

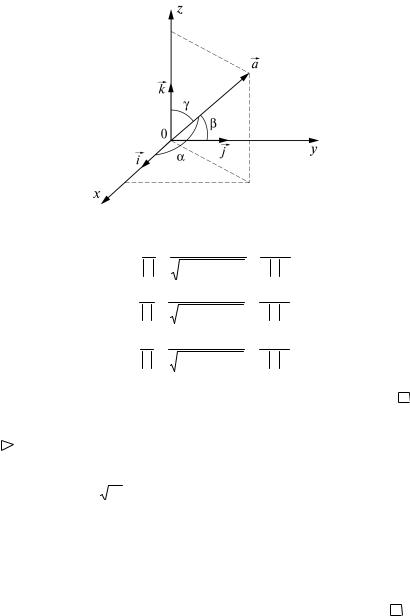
Рис. 3

Отсюда:

cos α

a!1

пр!a

;

a12 + a22 + a32

cosβ

пр !j a

;

a12 + a22 + a32

cos γ=

a!3

пр !a

;

a12 + a22 + a32

(cos2 α

+ cos2 β +

cos

2 γ) =

cos2 α +

cos2 β

cos2 λ

= 1.

a a

Пример 2.

Даны векторы

col (3; −

2; 1)

col

(− 1;1; − 2) .

= col (c1; c2 ; c3) ,

Найти вектор c

ортогональный векторам a

и b, если

его длина равна

35 .

Решение.

По

условию

ортогональности

векторов

имеем

3с1 – 2с2 + с3 = 0

и –с1 + с2 – 2с3 = 0.

Кроме

того,

по

условию

(с )2

+(с )2 +(с )2 = 35. Решая систему полученных трех уравнений, находим

c!1 =

col (3; 5;1) ,

c1 =

±3, c2

= ±5, c3

= ±1 .

Итак, имеем два

вектора

c!2 =

col (−

3; − 5; −

1) , которые удовлетворяют условиям примера 2.

3 6

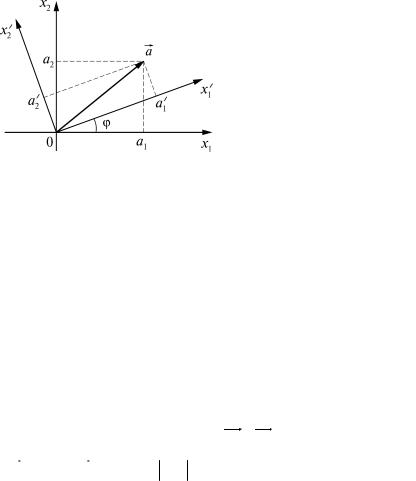
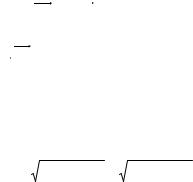
Рис. 4	Рис. 5
30. Проекции двумерного вектора	в повернутой си-

стеме координат. Пусть задан вектор в декартовой системе коор-

динат Ox1x2 в двумерном пространстве:

= a1i

a2 j .

Нужно найти проекции (координаты)

a′и

a′этого вектора в по-

вернутой на угол ϕ

системе координат Ox ′x′(рис. 4):

= a′i ′+

a′j ′,

где i!′, !j ′– орты новых координатных осей.

Из рис. 5 видно,

что

i! =

OA + OB =

cos ϕ

i!′− sin ϕ !j ′,

т.к.

cos ϕ ,

= sin ϕ ,

i!′=

!j ′= 1.

Аналогично, !j =

sin ϕ i!′+ cos ϕ

!j ′.

Таким образом,

a2(cos ϕ

+ a2 sin ϕ ) +

a =

a1 (cos ϕ i ′− sin ϕ

j ′)+

j ′+

sin ϕ i )′=

i ′(a1 cos ϕ

′(a

cos ϕ − a

sin

′.

ϕ ) = a′i ′+ a′j

Векторы равны, если равны их соответствующие проекции на оси i!′и !j ′:

a1′= a1 cos ϕ + a2 sin ϕ ,

a′=	a	2	cos ϕ − a	sin ϕ .
2		2	1

3 7

! Задания для самостоятельной работы

1.	Даны точки А (–1; 5; –10),				В (5; –7; 8), С (2; 2; –7), D (5; –4; 2).
Проверить, что векторы AB и CD коллинеарны. Во сколько раз один
из этих векторов длиннее другого?
2.	Найти прCD AB ,		если	А (1; –2; 3),			В (4; –4; –3), С (2; 4; 3),
D (8; 6; 6).								!
3.	Найти направляющие косинусы вектора
								a = col (2; − 1; 2) .
4.	Найти угол между диагоналями параллелограмма, построен-
	!	= col (2; 1; 0)		и	!	col (0; − 2; 1) .
ного на векторах a					b =
5.	Убедиться,	что	(a )2 + ( a )		2 =	(a′)2	+ ( a′) 2	, т.е. длина отрез-
			1	2		1	2

ка прямой при повороте не меняется.

6. Вычислить косинус тупого угла между медианами, проведенными из вершин острых углов равнобедренного прямоугольного треугольника.

7. Найти вектор	!				!	= col (1; − 2; 3) и
7. Найти вектор	c	, коллинеарный вектору a				= col (1; − 2; 3) и
удовлетворяющий условию			!	!	= 5 .
удовлетворяющий условию			c	a	= 5 .

Замечание 1. Дальше символ «col» будем опускать, если это не создает недоразумений.

3 8

Лекция 7

Матрицы и определители

Дается понятие матрицы, определителя квадратной матрицы, рассмотрены свойства определителей и правила их вычисления.

10. Понятие матрицы. Матрицей порядка m ×n (размерности m ×n) называют прямоугольную таблицу чисел или буквенных выражений, содержащую m строк и n столбцов:

A = (aij ) = a =

	a11
	a21
	"
	"
	am1
	am1

a12	$ a1n
a22	$ a2n
"	"	" .
am2
	$ amn

Квадратной матрицей называется матрица, у которой число строк равно числу столбцов.

Матрицы равны между собой, если равны все соответствующие

элементы этих матриц, т.е. A = B, если аij = bij при i = 1, m, j = 1, n . Транспонированной матрицей АТ называется такая матрица, у

которой все строки заменены соответствующими столбцами. В общем случае для квадратных матриц А ≠ АТ. Например,

A =

a11

a12

≠

a11

a12

≠ а21.

a21

, если а12

a22

Если А = АТ, то матрица А называется симметричной. Из Л.6 следует, что m-мерный вектор – это матрица, содержащая один столбец,

	a1		!
т.е.	"		!
т.е.	"	=	a. Матрицу, содержащую одну строку, называют транспо-

	am						!
нированным n–мерным вектором, т.е. (a ;a					;...;a		!
нированным n–мерным вектором, т.е. (a ;a				2	;...;a		) = aT .
			1	2		n
	Нулевой называется матрица, у которой все элементы равны
				=		0	0
нулю. Например, нулевая 2 2 –матрица 0				=			.

						0	0

3 9

20. Понятие определителей второго и третьего по-

рядка. По определенному правилу каждой квадратной матрице А можно поставить в соответствие число, которое называется определителем

(используют обозначения ∆ , det A, A ).

Если порядок матрицы равен единице, то она составлена из од-

ного элемента a11. Определителем первого порядка, который соответ-
ствует матрице A = (a11) , назовем число			a11 : ∆ = a11 .
Для квадратной матрицы	A =	a11	a12	назовем определителем

		a21
			a22

второго порядка число, которое равно разности произведений элементов главной диагонали и побочной:

∆ =	a11	a12	= a11 a22 − a21 a12 .	(1)
	a21	a22

Дальше будем называть элементами, строками, столбцами те элементы определителя A произвольного порядка, которые стоят на том же месте, что и соответствующие элементы, строки и столбцы матрицы А.

		a11		a12	a13
Для матрицы	A =		a21	a22	a23	определителем третьего поряд-

			a31	a32
					a33

ка назовем число, определяемое равенством:

∆ =

a11

a12

a13

= a11

a22

a23

−

a12

a21

a23

a13

a21

a22

a21

a22

a23

(2)

a31

a32

a33

Отметим, что для вычисления определителя третьего порядка используют алгебраическую сумму произведений элементов первой строки и определителей второго порядка из элементов второй и третьей строк.

Используя равенство (1), определение определителя третьего порядка (2) можно записать в другом виде:

4 0

<<< < Предыдущая 1 2 34 / 414 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.11.2018253.44 Кб9второй курсач(разработка)(Кристина)2.doc
#
13.09.201940.04 Кб6Вуліца Замкавая.docx
#
18.02.2016147.97 Кб2вучэбная праграма 2012.doc
#
19.02.201612.77 Mб65Высшая матем. Учебник.pdf
#
22.09.2019956.93 Кб18Высшая математика (1).doc
#
18.02.20165.88 Mб72высшая математика.pdf
#
18.02.2016192.33 Кб16Вычеты аналитических функций..pdf
#
18.02.2016190.98 Кб4гістарычная навука Бел. раб. праграма 2012.doc
#
14.04.2019380.93 Кб13Гісторыя Беларус(шпоры).doc
#
12.11.2019311.93 Кб3Гісторыя беларускага сялянства. Т.2..docx
#
15.04.2019130.2 Кб4гістрыя вся.docx