Анализ первичных статистик

Делать выводы о результатах диагностики можно также на основе анализа первичных статистик (т.е. статистических показателей) или описательных статистик. К ним относят среднее арифметическое, медиану, моду, размах, стандартное отклонение и некоторые другие. Эти статистики можно сравнивать между собой (например, среднее арифметическое значение тревожности в разных группах).

1. Среднее арифметическое чаще всего используют для анализа. Для несгруппированных данных формулу вы уже знаете (). Для сгруппированных по классовым интервалам данным вычисление средней арифметической производят по следующей формуле.

, где

X_i - центр i-того класса,

f_i – частота i-того класса,

n – количество испытуемых.

Среднее арифметическое – это статистический показатель, он чаще всего представлен дробным значением (например, тревожность = 17,42).

2. Медиана (Ме) – это не отдельное измерение, а точка в последовательном ряду данных на измерительной шкале, выше и ниже которой находятся по половине наблюдений¹³.

• Вычисление медианы для несгруппированных данных, упорядоченных по степени их возрастания или убывания.

а) нечетное количество результатов:

1, 4, 5, 7, 13, 14, 15, 17, 18, 19, 21, 24 Ме = 14

б) четное количество результатов:

1, 4, 5, 7, 13, 14, 15, 17, 18, 19, 21, 24 Ме = (14 + 15)/2 = 14,5

• Вычисление медианы для сгруппированных данных осуществляется по формуле:

  ,

  l – нижняя точная граница класса группировки,

  содержащего медиану;

  f_cum- сумма частот классов, нижеl,

  f_р– сумма частот класса, содержащего медиану;

  n– число показателей;

  i– ширина класса группировки.

Где где

Рассмотрим вычисление медианы на примере таблицы 8:

• Найдем половину наблюдений:

39 / 2 = 19,5

• Суммируем частоты (f), начиная с минимального класса группировки, до класса, содержащего половину представленных показателей (не менее 19,5), т.е. до медианы:

3+4+7+1+8 = 23

Медиана находится в 5 классе, точные границы которого 67,5 – 72,5;

• Определим f_cum, т.е. сумму частот предыдущих классов, в которые медиана не входит:

f _cum = 3+4+7+1 = 15

• Подставим данные в формулу:

Это означает, что ровно половина детей читают больше 70 слов в минуту.

3. Мода (Мо) - это показатель, наиболее часто встречающийся в выборке («модный»). Чаще всего ее определяют тогда, когда результаты представлены в номинативной шкале. Определяют ее по частоте проявления какого-либо признака. Покажу на примерах:

а) 1; 2; 1; 3; 3; 1; 3; 2; 2. (1 – праворукие, 2 – амбиверты, 3 - леворукие).

Диапазон	Частота (d)
1 2 3	3 3 3

В данном случае моды нет.

б) В тесте Люшера желтый цвет ставят в разные позиции: 24, 15, 13, 8, 15, 10, 9, 8

Позиция желтого цвета	Частота (d)
1 2 3 4 5 6 7 8	24 Мо = 1, т.е. чаще всего желтый цвет ставят в первую позицию. 15 13 8 15 10 9 8

в) 10, 12, 13, 14, 11, 12, 11, 15, 16, 12, 10, 11.

Диапазон	Частота (d)
16 15 14 13 12 11 10	1 1 Мо = (12 + 11)/2 = 11,5 1 1 3 3 2

г) 2, 4, 3, 5, 5, 4, 4, 2, 2, 4, 2 - отметки за контрольную работу.

Диапазон	Частота Мо = 4 и Мо = 2. В данном примере две моды
5 4 3 2	2 4 1 4

4. Размах (Wn) – это интервал между наибольшим и наименьшим значением. Определяется он как разность между максимальным и минимальным значениями (x_max – x_min). При малом количестве данных размах очень зависит от выступающих значений.

Например: 2, 5, 3, 1, 7, 5, 6, 4. 7 – 1 = 6

15, 17, 11, 10, 14, 13, 16, 100. 100 – 10 = 90

Однако во втором ряду значений 100, скорее всего, выпадающее значение (возможно описка). И если его исключить, размах будет гораздо уже: 17 – 10 = 7.

5. Стандартное отклонение () – также является первичной статистикой. Стандартное отклонение – это мера разнообразия показателей, входящих в группу. Оно показывает, на сколько в среднем отклоняется каждая варианта от средней арифметической. Чем больше отклонение, тем больше сигма.

Расчет стандартного отклонения для несгруппированных данных мы уже рассматривали (см. стр. 32, 39, 43). Для сгруппированных данных формула вычисления следующая:

f – частота отдельного интервала

n – количество результатов

Х – отклонение центра класса от среднего арифметического.

, где

Смотрите вспомогательную таблицу для расчета (табл.10).

Таблица 10.

Расчет стандартного отклонения для сгруппированных данных.

Классовые интервалы	Центр класса (xj)	Частота (f)	Отклонение (Х) | xј – M |	Х²	fХ²
55-59	57	1	25,09	629,508	629,508
50-54	52	2	20,09	403,608	807,216
45-49	47	4	15,09	227,708	910,832
40-44	42	6	10,09	101,808	610,848
35-39	37	8	5,09	25,908	207,264
30-34	32	11	0,09	0,008	0,088
25-29	27	9	4,91	24,108	216,972
20-24	22	7	9,91	98,208	687,456
15-19	17	5	14,91	222,308	1111,540
10-14	12	2	19,91	396,408	792,816
		n = 55			fХ² = 5974,54

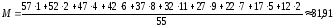
Давайте покажу Вам один фокус. Посмотрите на значение стандартного отклонения в последнем примере и примере со стр. 39.

 = 10,422; _интел= 6,56;_нейрот= 3,31.

Что можно сказать о разбросе значений по данным показателям? Ни–че–го! Ничего нельзя сказать по абсолютным значениям стандартного отклонения, так как показатели измерены в разных единицах. Чтобы сравнить отклонения в распределении значений разных показателей, необходимо применить коэффициент вариации. С помощью него величина сигмы приводится к одному масштабу.

CV- коэффициент вариации,

 - стандартное отклонение,

M- среднее арифметическое.

, где

Сравним изменчивость массивов данных:

1) = 10,42;М= 31,91;

2) _интел= 6,56;М= 101,2;

3) _нейрот= 3,31;М= 14,5;

Посмотрите, если по абсолютному значению разброс данных выше по шкале нейротизма, то, посмотрев на приведенные в один масштаб значения, видно, что он оказывается средним. Самый низкий разброс показателей – по шкале интеллекта.

Итак, проведя первичную обработку эмпирических данных (т.е. полученных в результате Вашего опыта), Вы сделали соответствующие выводы о распределении показателей, о средних значениях, о разбросе данных. Но это только первичная обработка данных. Методы математической статистики в психолого-педагогическом исследовании используют и для решения более сложных задач. И это будет вторичная обработка данных.

вторичная ОБРАБОТКА ДАННЫХ

Благодаря вторичной обработке данных можно выявить скрытые тенденции, закономерности и связи; обнаружить новые факты, которые не ожидались и не были замечены в ходе эмпирического процесса; выявить уровень достоверности, надежности и точности полученных результатов; получить научно обоснованные результаты. Выбор конкретного метода обработки данных зависит от задач исследования, а также от способа измерения данных (т.е. шкалы, в которой они представлены).

Изучите внимательно таблицу 11.

Таблица 11

Классификация задач и методов их решения (на базе таблицы Е.Ф. Волковой).

№ п/п	Задачи	Условия	Объем выборки (ок)	Методы	Шкала
1	2	3	4	5	6
1	Отбраковка выпадающих значений	нет ограничений	n5	t – критерий выпада
2	Определение наиболее характерных показателей для исследуемой выборки	нет ограничений	чем больше выборка, тем ближе может быть оценка параметра к его истинному значению	x-среднее арифметическое	интервальная отношений
				Ме– медиана	порядковая интервальная отношений
				Мо- мода	чаще для номинативной
3	Оценка степени рассеивания отдельных величин вокруг средней арифметической	нет ограничений	чем больше выборка, тем ближе может быть оценка параметра к его истинному значению	Wn – размах	порядковая интервальная
		точно для нормального распределения		 - стандартное отклонение	отношений интервальная отношений
4	Выявление различий в уровне исследуемого признака	2 выборки испытуемых, диапазоны разброса показателей не должны совпадать	n≥ 11, n1  n2	Q–критерий Розенбаума	порядковая интервальная отношений
		2 выборки испытуемых, имеется зона перекрещивающихся значений между выборками (т.е. повторяющихся в разных выборках).	а) n1=2,n25 б) 3 ≤ n1 ≤ 60, 3 ≤ n1 ≤ 60,	U–критерий Манна-Уитни	порядковая интервальная отношений
		2выборки испытуемых	а) n1=2,n230 б) n1=3,n27 в) n1=4,n25 г) n1, n25	φ*-критерий (угловое преобразование Фишера)	любая шкала
5	Оценка различия в средних	2 выборки испытуемых, нормальное распределение	30(n1 +n2 -2) до 	t – критерий Стьюдента	интервальная отношений
1	2	3	4	5	6
6	Оценка сдвига значений исследуемого признака	Одни и те же показатели, измеренные у одних и тех же испытуемых до и после воздействия а) при отсутствии контрольной группы (2 замера 1 группа)	5  n  50	Т– критерий Вилкоксона	порядковая интервальная отношений
		б) при наличии контрольной группы (2 замера 2 группы)	5  n  50	Вариант1– сопоставление значений «до» и «после» отдельно по экспериментальной и контрольной группам Т – критерий Вилкоксона	порядковая интервальная отношений
			n  11, n1  n2 n1=2, n2  5; 3  (n1, n2)  60 n1, n2  5	Вариант 2– сопоставление сдвигов в двух группах Q– критерий Розенбаума U– критерий Манна–Уитни φ*-критерий Фишера	порядковая интервальная отношений все шкалы
7	Выявление различий в распределении признака	сопоставление двух эмпирических распределений или эмпирического с теоретическим	n30	² критерий Пирсона	любая шкала
			n1,2 50	-критерий Колмогорова-Смирнова	порядковая интервальная отношений
			а) n1=2,n230 б) n1=3,n27 в) n1=4,n25 г) n1, n25	φ*-критерий Фишера	любая шкала.
8	Выявление степени согласованности изменений (корреляции)	2 признака или 2 профиля	30< n  40	rs-коэффициент ранговой корреляции Спирмена	порядковая интервальная отношений
			4< n5000	rxy-коэффициент линейной корреляции Пирсона	интервальная отношений

С описанием способа решения первых трех задач Вы познакомились, изучая раздел «Первичная обработка данных».

Для дальнейшего рассмотрения способов обработки данных нам потребуется понятие «статистические гипотезы». Формулирование гипотез систематизирует предположения исследователя и представляет их в четком и лаконичном виде. Благодаря гипотезам, исследователь не теряет путеводной нити в процессе рассчетов и ему легко понять после их окончания, что, собственно, он обнаружил. Статистических гипотез две:

• нулевая гипотеза(Н_о) – гипотеза об отсутствии различий, эту гипотезу мы опровергаем, если стоит задача доказать значимость различий,

• альтернативная гипотеза(Н₁) – это то, что мы хотим доказать.

Для каждого метода статистической обработки данных эти гипотезы в общем виде будут сформулированы. Вам придется только уточнить их в терминах Вашего исследования.

Итак, определитесь, какую задачу Вам необходимо решить, выберите по таблице подходящий метод, четко следуйте алгоритму подсчета данных – и у Вас все получится! Небольшая рекомендация: независимо от того, считаете ли Вы «в столбик» или на калькуляторе – пересчитывайте все операции не менее двух раз, тогда Вы снизите риск механической ошибки.

ВЫЯВЛЕНИЕ РАЗЛИЧИЙ В УРОВНЕ ИССЛЕДУЕМОГО ПРИЗНАКА

Такая задача стоит перед нами тогда, когда необходимо сопоставить между собой данные двух групп, чтобы доказать, что группы различны (например, различия между экспериментальной или контрольной группами после проведенного Вами воздействия), либо что между группами нет различий (на этапе предварительной диагностики экспериментальной и контрольной групп).

Возможна другая ситуация: изначально у Вас большая выборка, скажем человек 60, упорядоченная по какому-либо показателю. Из этой группы Вам необходимо выделить подгруппу с высокими значениями по данному показателю и подгруппу с низкими значениями, чтобы сравнить и другие данные в этих подгруппах. Например, Вы продиагностировали испытуемых и упорядочили их по показателю тревожность. Вам необходимо посмотреть, существуют ли различия в уровне самооценки у высокотревожных и слаботревожных. Если вы разделите всю группу пополам, то среднее значения «смажут» Вам всю картину. В подобном случае лучше группу делить не на 2, а на 3 подгруппы, и брать в расчет только «крайние» подгруппы. В среднюю подгруппу попадут те, чьи показатели отклоняются от средней арифметической не более, чем на ¼(М¼). При этом Вы потеряете около 19,8 % испытуемых при нормальном распределении, и больше, если распределение отличается от нормального.

Итак, у Вас две группы и перед Вами стоит задача определить, достоверны ли различия между ними по исследуемому признаку.

Q – критерий Розенбаума

Это очень простой критерий, который позволяет быстро оценить различия между двумя выборками. Однако если критерийQне выявляет достоверных различий, это еще не означает, что их действительно нет.

Статистические гипотезы:

Но: уровень признака в выборке 1 не превышает уровня признака в выборке 2.

Н1: уровень признака в выборке 1 превышает уровень признака в выборке 2.