36

Таким образом, условиям задачи отвечают две площадки, показанные на рис. 3.2, а.

3. Определим нормальные напряжения на площадках n1 и n2 по формуле (3.1)

σα1 = σ1 cos2 α1 = 50cos2 19o55′ = 42,27 МПа,

σα2 = σ1 cos2 α2 = 50cos 70o5′ = 5,75 МПа.

Так как полные напряжения равны геометрической сумме составляющих τ2 и σ2 , то получим

pα1 = 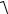σα2 1 + τα2 = 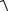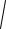44,272 +162 = 47,07 МПа, pα2 =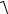 σα2 2 + τα2 = 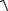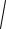5,752 +162 =17,0 МПа.

На рис. 3.2, а показаны напряжения, действующие на площадках n1 и n2 , все напряжения оказались положительными.

II. Графическое решение задачи

Графическое решение осуществляется с помощью круга Мора. Круг Мора представляет собой окружность, построенную в осях σ, τ,

где ось σ - ось абсцисс, ось τ - ось ординат (рис. 3.2, б).

Каждой точке круга Мора соответствует площадка в точке тела. Координаты точки круга есть нормальное и касательное напряжения, действующие на площадке, которой соответствует точка круга. Так, одной из главных площадок в точках растянутого стержня, на которой

действуют напряжения σ1>0, τ = 0, соответствует точка круга М1 (σ1, 0); второй главной площадке, где σ2 = 0, τ = 0, соответствует точка М 2 (0, 0); площадке n1 c напряжениями σα1 , τα1 (рис. 3.2, а) соответствует точка круга Мn 1 (σα1 , τα1 ) и т.д. Причем, оказывается, что точки

круга, соответствующие взаимно перпендикулярным площадкам, расположены на концах диаметра круга.

Поэтому отрезок М2 М1 (рис. 3.2, б) является диаметром круга Мора при растяжении. Тогда середина М2 М1 есть центр круга С, абс-

38

Графическое решение получим, проведя линию, ордината которой равна заданному t = 16 МПа. Эта линия пересечет круг Мора в точках Мn1 и Мn2 , соответствующих площадкам n1 и n2 в стержне, абсциссы

этих точек σα1 и σα2 совпадают со значениями напряжений в аналити-

ческом решении.

Кроме того, углы между радиусами круга СМ1 и СМn2 равны 2a1

и 2a2, причем с аналитическими результатами совпадают как величины, так и направления отсчетов углов (против часовой стрелки).

Таким образом, результаты аналитического и графического решений совпадают.

3.2. Плоское напряженное состояние

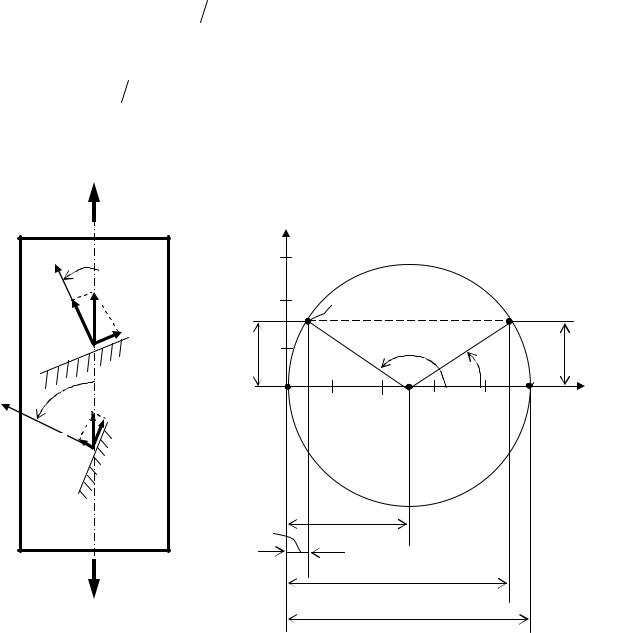
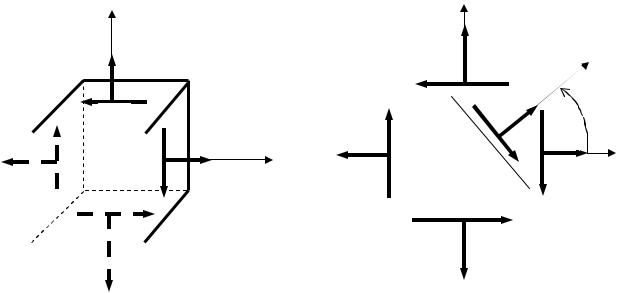
Если при плоском напряженном состоянии все напряжения в точке тела (рис. 3.3, а) известны напряжения, действующие по двум взаимно перпендикулярным площадкам, то можно найти напряжения по любой площадке в точке тела. На рис. 3.3, б показана произвольная пло-

щадка «n», внешняя нормаль которой составляет с осью х угол a (угол положительный, так как откладывается против часовой стрелки). Нормальное σn и касательное τn напряжения на площадке n определяются

площадках х, у.

Заметим, что производная функции σn (a) по переменной a равна по модулю удвоенному значению τn

39

Рис. 3.3. Напряжения на площадках х и у в точке тела при плоском напряженном состоянии (а), напряжения

на площадках х, у и на площадке n (б)

Из формул (3.2) следует, что σn =σn (α) и τn =τn (α) являются функциями угла α. При изменении угла α функция τn (α) обращается в нуль при двух значениях угла α1 и α2 . Следовательно, площадки α1 и α2 являются главными площадками. Нормальные напряжения на этих площадках есть главные напряжения, причем, учитывая (3.2), главные напряжения есть экстремумы функции σn (α). Проверка экстремумов по

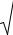
40

Второй угол, определяющий положение второй главной площадки, отличается от первого на 90о .

Обозначив углы α1 и α2 , получим α1 = α0 , α2 = α0 + 90о . Известна формула для определения главных напряжений при ПНС

Главные напряжения единственные в точке тела, поэтому их сумма является величиной, равной сумме нормальных напряжений на любых двух взаимно перпендикулярных площадках.

Сложим σmax и σmin из (3.5), получим

σmax + σmin = σx + σy = const.

Если известны главные напряжения σmax и σmin , то целесообраз-

но с их помощью определять напряжения, действующие по произвольной площадке n.

Обозначим угол между внешней нормалью к площадке «n и линией действия σmax через β (знак β определяется так же, как знак угла α).

Тогда формулы (3.2) могут быть представлены в виде

С помощью (3.2), (3.4), (3.5), (3.6) строится аналитическое решение двух основных задач плоского напряженного состояния: определение главных напряжений, если известны напряжения, действующие по двум взаимно перпендикулярным площадкам, и определение напряжений по любой площадке, если известны главные напряжения.

Однако возможно и графическое решение этих задач с помощью круга Мора. Представление о круге Мора при плоском напряженном состоянии принципиально не отличается от рассмотренного при линейном напряженном состоянии.

41

Построение круга Мора обычно осуществляется по двум его точкам, соответствующим двум взаимно перпендикулярным площадкам. Эти точки расположены на одном диаметре круга.

Так как в силу закона парности касательных напряжений точка

пересечения диаметра с осью σ есть центр круга, то нетрудно построить круг Мора.

Точки пересечения окружности с осью σ соответствуют главным площадкам. Абсциссы этих точек равны двум главным напряжениям по величине и знаку. Учитывая, что главных напряжений в общем случае в точке три, причем при плоском напряженном состоянии одно из них равно нулю, необходимо указать, какое из полученных напряжений является первым, вторым или третьим, принимая во внимание соотноше-

ние s1 ³ s2 ³ s3.

Линии действия главных напряжений, а значит, и положение главных площадок получают с помощью точки круга Мора, называемой полюсом. Отыскание полюса и его использование показано в примере, рассмотренном ниже.

Один из вариантов графического решения второй задачи основан на том, что угол между радиусами, проведенными в точки круга Мора, равен удвоенному углу между двумя площадками в точке тела, соответствующими точкам круга. Если задан угол между s1 и нормалью к ис-

комой площадке, то на круге Мора проводят радиус под углом к радиусу СМ1, равный удвоенному заданному, и получают точку круга, соответствующую искомой площадке. Координаты точки круга Мора есть нормальное и касательное напряжения, действующие на искомой площадке точки тела. При этом учитывается знак угла: положительный угол откладывается против часовой стрелки. Так, на рис 3.2, б определены точки Мn1 и Mn2 с помощью положительных углов 2α1 и 2α2.

Пример 3.2.

Задана схема площадок в точке тела (рис. 3.4, а) в условиях плоского напряженного состояния. Напряжения равны sа = 60 МПа,

sв = 30 МПа, tв = 20 МПа. Требуется определить главные напряжения и положение главных площадок.

I.Аналитическое решение задачи

1.В условии задачи не заданы взаимно перпендикулярные площадки с напряжениями на них. Поэтому вначале необходимо образо-

42

вать такие площадки и найти соответствующие напряжения. Назовем площадку с напряжением σа площадкой у, тогда σу = σа . Образуем

площадку х с напряжениями σх и τух , пока неизвестными. Для их определения воспользуемся заданными напряжениями σв и τв .

Угол α, отсчитываемый от линии оси х до внешней нормали к площадке, по которой действует напряжение σв (или, что то же до ли-

нии действия τв ), равен +30о , как видно из рисунка. Подставим значения напряжений и угла в формулы (3.2):

Решив последние два уравнения совместно относительно σх и τух , получим σх = 63,09 МПа, τух = 37,32 МПа..

2. Определим главные напряжения по формуле (3.5)

σmax = 61,54 + 37,35 = 98,89 МПа = σ1,

σmin = 61,54 − 37,35 = 24,19 МПа = σ2 ,

σ3 = 0.

44

3.Установим положение главных площадок с помощью формулы (3.4)

2a0 = -87о30¢, отсюда

a1 = -43о45¢¢,

a2 = a1 + 90о = + 46о15¢.

4.Проверим линию действия какого главного напряжения определяет угол α0 с помощью второй производной

dd2s2n = -2(63,21- 60)cos(- 2 × 43o45¢)+ 4 ×37,59sin(- 2 × 43o45¢)< 0. a

Следовательно, угол α0 определяет линию действия σmax .

5. Покажем на рис. 3.4, а главные направления I и II. Для этого от оси х откладываем угол α1 по часовой стрелке (отрицательный угол),

угол α2 против часовой стрелки (положительный угол). Главные пло-

щадки перпендикулярны этим направлениям (они показаны внутри заданного элемента). Там же показаны главные напряжения.

II.Графическое решение

1.Строим круг Мора по двум точкам Мх (sx, tyx) и М у (σ у , τ ху ),

соответствующим площадкам х и у.

Координаты точек σx = 63,09 МПа, τ yx = 37 , 32 МПа ,

45

σу = 60,0 МПа, τху = −τух = −37,32 МПа.

Отрезок, соединяющий точки Мх и М у , есть диаметр круга с цен-

тром на оси σ. Остается построить окружность.

Точки М1 и М2 соответствуют первой и второй главным площадкам величины σ1и σ 2 , в соответствии с масштабом построения совпа-

дают с результатами аналитического решения.

2. Главные направления получим с помощью полюса круга Мора. Чтобы получить полюс, из т. М у опускаем перпендикуляр к оси σ и

продолжаем его до пересечения с окружностью. Точка пересечения называется полюсом, обозначим ее А.

Проведя из т. А лучи в точки М1 и М2 , получим главные направ-

ления I и II. Сравнивая полученный результат с рис. 3.4, а, убеждаемся в их совпадении с аналитическим решением.

Пример 3.3.

Даны главные площадки в условиях плоского напряженного состояния и главные напряжения, действующие на этих площадках σmax = 100 МПа, σmin = −50 MПа. Необходимо определить напряжения

на двух площадках: одна из них расположена под углом

β= −30о (от σmax ), а вторая – под углом θ = 30о (от σmin ) (рис.3.5, а, б).

I.Аналитическое решение задачи

1.Определим напряжения на площадке β = −30о с помощью формул (3.6)

1. Определим напряжения на площадке θ = +30о (от σmin ) .

46

Так как в (3.6) положение любой площадки определяется только по отношению к площадке σmax, то необходимо найти угол между первым

главным направлением и линией, проведенной под углом +30о к третьему главному направлению.

а)

в)

σmin=σ3

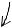β= -30о

β1=-60о

Рис. 3.5. Главные площадки и внешние нормали к площадкам β, θ (а); главные площадки и площадки β, θ с напряжениями на них (б); круг Мора для определения напряжений на площадках β, θ (в)

Из рис. 3.5, а видно, что этот угол равен β1 = −60о . Тогда

σθ = 100 +2(− 50) + 100 −2(− 50)cos 2(− 60o )= −12,5 МПа,

47

tθ = 100 − (− 50)sin 2(- 60o )= 64,95 МПа. 2

II.Графическое решение задачи

1.Построим круг Мора по двум точкам, соответствующим

(σ3 = σmin = −50 МПа ). Ординаты этих точек равны нулю, так как касательные напряжения на главных площадках отсутствуют (рис. 3.5, а).

Таким образом, обе точки М1 и М3 лежат на оси s, а центр круга расположен посредине между ними. От радиуса круга СМ1 откладыва-

ем угол -2×30 = -60о по часовой стрелке, получаем точку Мβ, координаты которой равны σβ и τβ . Затем от СМ1 откладываем угол 2(-60) = – 120, получаем точку Мθ с координатами σθ и τθ (либо, как показано

на рис. 3.5, в, от радиуса СМ3 откладываем угол, равный 2(+30) = +60о, и вновь получаем точку Мθ).

Значения напряжений по величине и знаку совпадают со значениями, найденными аналитически.

3.3. Обобщенный закон Гука

Если материал следует закону Гука, а деформации малы, то зависимость между напряжениями и деформациями в общем случае объемного напряженного состояния выражается формулами, называемыми обобщенным законом Гука

где ε1,ε2 ,ε3 – главные относительные деформации в направлении напряжений σ1 ,σ2 ,σ3 ; Е и m – модуль упругости и коэффициент Пуассона материала конструкции соответственно.