140

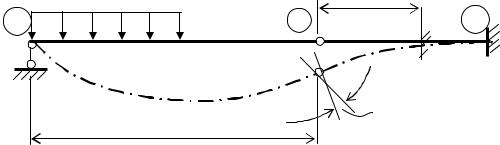
Если балка составная, то есть состоит из нескольких дисков, соединенных шарнирами (рис. 6.11), то функция θ(z) в месте шарнирного соединения (I) будет испытывать разрыв (скачок) величиной Δθi.

Учет таких соединений может быть выполнен введением в уравнение θ(z) (6.14) слагаемого θi (z − di )0 , а в уравнение v(z) (6.15) - θi (z − di ). Величины угла поворота θ(0) и прогиба v(0) в начале координат называют кинематическими начальными параметрами. Кинема-

тические параметры v(0), θ(0) и Δθi определяются с помощью кинематических граничных условий задачи.

Рис. 6.11. Учет сквозных шарниров

Эти условия должны учитывать наложенные на балку связи. Например, для балки, представленной на рис. 6.10, будут равны нулю угол поворота и прогиб в заделке (θ( ) = θA = 0 и v( ) = vA = 0), а для бал-

ки на рис. 6.11 – соответственно v(0) = 0; θ( ) = 0; v( ) = 0. Отметим

особо, что количество граничных условий всегда должно быть равно количеству кинематических параметров v(0),θ(0) и θi .

При использовании уравнений (6.12), (6.13) и (6.14) удобно применять «правило отрицательного аргумента». Это значит, что значения сложных аргументов вида (z - ai), (z - bi) и т.д. всегда должны быть положительными. Если значения этих аргументов становятся отрицательными, то слагаемое, содержащее такой аргумент, надо отбросить (приравнять нулю).

Пример 6.2.

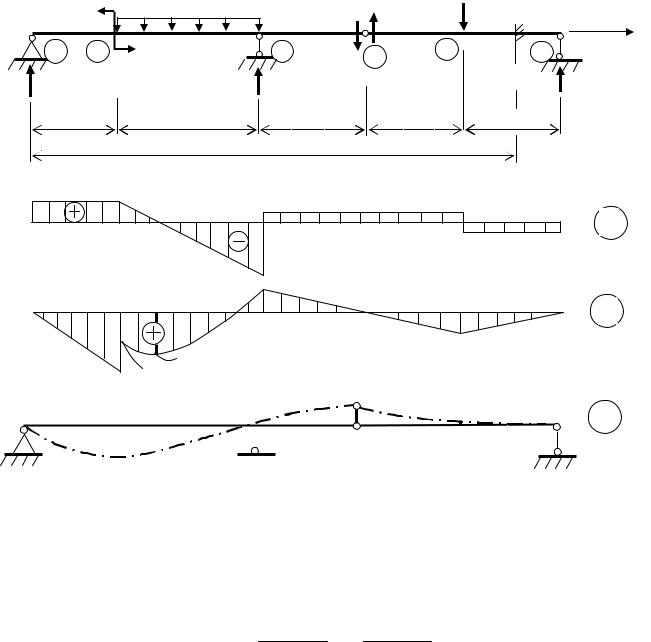
Для балки, изображенной на рис. 6.12, найти перемещения и построить изогнутую ось. Материал балки – Ст.3. Поперечное сечение из прокатного двутавра №20.

141

Определение опорных реакций и внутренних усилий здесь не обсуждается, а результаты построения эпюр приведены на рис. 6.12, а, б.

Модуль упругости Ст.3 Е = 2×105 МПа, момент инерции поперечного сечения балки J = 1840 см4. Жесткость поперечного сечения при изгибе

ЕJ = 2×108×1810×10-8 = 3,62×103 кН×м2. Статические начальные параметры Q(0) = 19,6 кН; M(0) = 0.

12

M

v

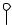
0,64 2,13

Рис. 6.12. Определение перемещений при изгибе Универсальное уравнение изгибающих моментов

M(z) = Q(0) z - M(z - 2)0 - q (z - 2)2 + q (z - 5)2 + VD (z - 5) - Р(z - 9). 2 2

142

Универсальное уравнение углов поворота

= 17,47 ×10−3 рад.

Для построения изогнутой оси балки найдем перемещения в некоторых сечениях:

+17,47 ×10−3 × 2 = -0,64 ×10−2 м = -0,64 см.

По результатам выполненных расчетов построена изогнутая ось балки – эпюра прогибов v (рис. 6.12, в). Из рисунка видно, что максимальный прогиб vmax = f ≈ 2,13см. Относительный прогиб составляет

f = 11002,13 = 5161 .

6.7.Определение перемещений методом Максвелла – Мора

Впрактике инженерных расчетов при изгибе, а также при других типах работы конструкций относительно редки случаи, когда есть возможность получить общие выражения для перемещений произвольного сечения стержневой конструкции. Как правило, при расчетах реальных конструкций необходимо знание перемещений отдельных заданных се-

144

чений. В таких ситуациях удобно применять метод Максвелла – Мора, основанный на энергетических принципах механики. Порядок решения задачи методом Максвелла – Мора (МММ) может быть сгруппирован в три основных этапа.

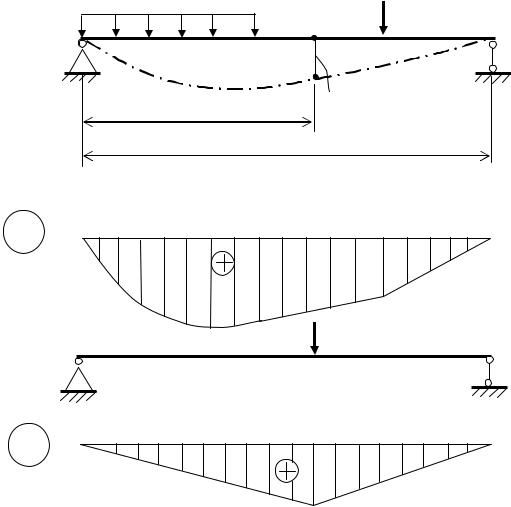
На первом этапе определяют внутренние усилия и строят их эпюры. При прямом изгибе простых балок и балочных систем основным усилием является изгибающий момент. Состояние конструкции под действием заданной расчетной нагрузки называется грузовым, а эпюра изгибающих моментов в этом состоянии MP(z) – грузовой (рис. 6.13, а).

MP

Рис. 6.13. Грузовое (а) и единичное (б) состояния в методе Максвелла - Мора

На втором этапе формируется вспомогательное единичное состояние, когда к конструкции прикладывается единичное воздействие в

145

месте искомого перемещения Dip (рис. 6.13, б). Если Dip является линей- ным перемещением (прогибом v), то воздействие осуществляется силой

Pi =1, направленной вдоль искомого перемещения (в рассматриваемом

случае по вертикали). Если искомое перемещение Dip - угловое, то есть угол поворота qi, то единичное загружение осуществляется парой Mi = 1. После этого определяются единичные изгибающие моменты Mi

и их эпюры.

На третьем этапе производится вычисление искомого перемещения по формуле Максвелла – Мора

Отметим, что формула (6.16) является усеченной, то есть учитывает влияние только изгибающих моментов. Практика показывает, что в абсолютном большинстве случаев влияние поперечных сил Q(z) пренебрежимо мало. В случае сложного сопротивления прямого стержня формула Максвелла – Мора имеет шесть слагаемых, каждое слагаемое учитывает одно из внутренних усилий (N, Qx, Qy, Mx, My, Mk).

Обычно одна из эпюр (чаще всего единичная) имеет линейный вид. В этом случае можно упростить вычисление определенного интеграла (6.15) и свести эту процедуру к простым численным операциям. Одним из таких приемов является правило Верещагина, которое заклю-

чается в следующем: если одна из эпюр моментов (далее Mi ) линейна (рис. 6.14, а), то интеграл Максвелла-Мора численно равен произведению площади эпюры грузовых моментов wр на ординату Mic единичного момента, взятую под центром тяжести wp:

В общем случае сложная эпюра грузовых моментов может быть разбита на n простых частей по принципу, проиллюстрированному на рис. 6.14, б. Тогда нахождение перемещения сведется к процедуре «перемножения» эпюр

146

В методе Максвелла-Мора положительный знак перемещения Dip означает, что оно совпадает по направлению с единичным фактором Pi = 1 или Мi = 1.

Рис. 6.14. Расчетная схема к применению правила Верещагина (а) и способ расслоения грузовой эпюры (б)

Значения площадей w на рис. 6.14 определяются по следующим формулам

Пример 6.3.

Для балки, показанной на рис. 6.15, определить перемещения методом Максвелла – Мора и построить ее изогнутую ось. Жесткость по-

перечного сечения принять 2×104 кН×м2.

Определим прогиб и угол поворота сечения «1». Грузовая эпюра изгибающих моментов, единичные состояния «1» и «2» и единичные эпюры изгибающих моментов показаны на рис. 6.15.