12. Непрерывные св. Плотность вероятностей и ее свойства.

Определение. Случайная величина , заданная на вероятностном пространстве, называетсянепрерывной или имеющей непрерывный закон распределения, если существует такая функция 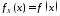, что для любогофункция распределенияслучайной величины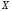допускает представление:. (2.3)

При этом функция называетсяплотностью вероятностей (плотностью распределения вероятностей, плотностью распределения) случайной величины .

Замечание. Для существования интеграла (2.3) предполагается, что плотность вероятностей является функцией непрерывна всюду, за исключением, может быть, конечного числа точек.

Из определения следует:

1. Если случайная величина является непрерывной, то ее функция распределениянепрерывна на всей числовой прямой.

(Это следует из свойств интеграла с переменным верхним пределом).

Следствие. Если случайная величина является непрерывной, то

для любого . (2.4)

2. Если случайная величина является непрерывной, то ее функция распределенияявляетсядифференцируемой во всех точках, где плотность вероятностей непрерывна, и при этом справедливо равенство:. (2.5)

В точках, где плотность вероятностей непрерывной не является, производная функции распределенияне существует. Это означает, что в этих точках функция распределения, являясь функцией непрерывной, имеетизлом, так что . Но таких точек в соответствии с замечанием не более конечного числа и в них плотность вероятностей может быть задана произвольно (на величине интеграла (2.3) и на вероятностях событий, связанных со случайной величиной, в соответствии с (2.4) это никак не отражается).

Замечание. Говорят также, что равенство (2.5) выполняется «почти всюду» или «для почти всех », понимая под этим справедливость равенства «везде» или «для всех», кроме (возможно)из некоторого множества нулевой меры (длины). Используя данную терминологию, можно сказать, что функция распределения непрерывной случайной величины является дифференцируемой почти всюду.

Геометрическая иллюстрация.

Из равенства (2.5) и определения производной следует, что.

Свойства плотности вероятностей

f1). Плотность вероятностей является функцией неотрицательной:для любого.

▲ Поскольку функция распределения является функцией неубывающей, то ее производная. Поэтому свойство следует из равенства (2.5) ■.

f2). Площадь под графиком плотности вероятностей равна единице:.

▲ Из представления (2.3) следует, что , а в соответствии со свойствомF2) функции распределения ■.

f3). Вероятность попадания непрерывной случайной величиныв интервалопределяется как интеграл от плотности вероятностей по этому интервалу: для любых

. (2.6)

▲ Поскольку в соответствии со свойством F6) функции распределения , то данное свойство непосредственно вытекает из представления (2.3):

■.

Следствие. Для непрерывной случайной величины

и все вероятности определяются с помощью интеграла (2.6).

Графическая иллюстрация функции распределения и плотности вероятностей непрерывной случайной величины.

13. Важнейшие непрерывные св.

1. Равномерная случайная величина.

Говорят, что непрерывная случайная величина имеет равномерный закон распределения (равномерное распределение) на отрезке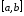, если множество ее возможных значений, а плотность вероятностей постоянна на этом отрезке:

Константа С при этом однозначно определяется из условия нормировки:

, то есть .

Таким образом, равномерно распределенная случайная величина имеет плотность вероятностей:

и для нее используется сокращенное обозначение: .

Найдем функцию распределения случайной величины .

Для этого рассмотрим три случая:

а) если , то;

б) если ,то;

в) если , то.

Окончательно имеем: и

Графики плотности вероятностей и функции распределения случайной величины имеют вид:

2. Показательная (экспоненциальная) случайная величина.

Говорят, что непрерывная случайная величина имеет показательный закон распределения (показательное, экспоненциальное распределение), если множество ее возможных значений, а плотность вероятностей имеет вид: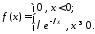

Число называется параметром показательного закона распределения, а для показательной случайной величины используется сокращенное обозначение:.

Проверим условие нормировки: при любом .

Найдем функцию распределения случайной величины .

Для этого рассмотрим два случая:

а) если 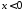, то;

в) если , то.

Окончательно имеем:

Графики плотности вероятностей и функции распределения случайной величины имеют вид:

3. Нормальная (гауссовская) случайная величина.

Говорят, что непрерывная случайная величина имеет нормальный закон распределения (нормальное, гауссовское распределение) с параметрами, если множество ее возможных значений, а плотность вероятностей имеет вид:

.

Сокращенное обозначение нормальной случайной величины:

.

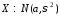Кривая плотности вероятностей имеет симметричный вид относительно прямой и имеет максимум в точке.

Проверим условие нормировки:

для любых значений параметров а и (при этом использовался известный в анализе факт, что- интеграл Пуассона).

5. Случайная величина, имеющая закон распределения Коши.

Говорят, что непрерывная случайная величина имеет закон распределения Коши, если множество ее возможных значений, а плотность вероятностей имеет вид:

.

Функция распределения случайной величины, распределенной по закону Коши, имеет вид:

.

Графики плотности вероятностей и функции распределения случайной величины, распределенной по закону Коши, выглядят следующим образом: