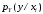- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
Известно,
что, если случайные события А
и В
зависимы, то условная вероятность
события А
отличается от его безусловной вероятности.
В этом случае
 .
.
Аналогичное положение имеет место и для случайных величин.
Пусть
 и
и - зависимые случайные величины,
- зависимые случайные величины, - их совместная функция распределения.
Если известно, что случайная величина
- их совместная функция распределения.
Если известно, что случайная величина уже приняла некоторое значениеy,
то закон распределения случайной
величины
уже приняла некоторое значениеy,
то закон распределения случайной
величины
 при этом условии не будет совпадать с
ее безусловным законом распределения.
Он называетсяусловным
законом распределения
случайной величины
при этом условии не будет совпадать с
ее безусловным законом распределения.
Он называетсяусловным
законом распределения
случайной величины
 при условии, что
при условии, что ,
и, заданный для всех возможных значенийy
случайной величины
,
и, заданный для всех возможных значенийy
случайной величины
 ,
полностью определяет зависимость между
случайными величинами
,
полностью определяет зависимость между
случайными величинами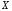 и
и .
.
Исчерпывающей
характеристикой условного закона
распределения случайной величины
 при условии, что
при условии, что ,
являетсяусловная
функция распределения
,
являетсяусловная
функция распределения
 случайной величины
случайной величины при условии, что
при условии, что ,
которую естественно было бы определить
следующим образом:
,
которую естественно было бы определить
следующим образом: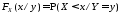 .
(3.12)
.
(3.12)
Следует
отметить, что это определение не имеет
смысла, если
 ,
что имеет место всегда, когда
,
что имеет место всегда, когда является непрерывной случайной величиной.
Тем не менее, в дискретном случае
определением (3.12) можно вполне пользоваться.
является непрерывной случайной величиной.
Тем не менее, в дискретном случае
определением (3.12) можно вполне пользоваться.
Пусть
 - дискретный случайный вектор,
- дискретный случайный вектор,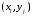 - его возможные значения,
- его возможные значения, - вероятности значений,
- вероятности значений,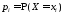 ,
, ,
,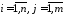 (случай счетного числа значений
дискретного случайного вектора
рассмотреть самостоятельно). Тогда все
условные законы распределения случайной
величины
(случай счетного числа значений
дискретного случайного вектора
рассмотреть самостоятельно). Тогда все
условные законы распределения случайной
величины при условии, что
при условии, что ,
, ,
являются дискретными и согласно
определению условной вероятности
имеем:
,
являются дискретными и согласно
определению условной вероятности
имеем: .
.
Дискретные
условные законы распределения удобнее
задавать не условной функцией распределения
 ,
а совокупностью условных вероятностей
,
а совокупностью условных вероятностей ,
заданных при каждом
,
заданных при каждом :
:

и записывать в виде таблицы:
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что при этом выполняется условие нормировки:
 .
.
Аналогичны
выражения для условной функции
распределения
 ,
условных вероятностей
,
условных вероятностей и дискретного условного закона
распределения случайной величины
и дискретного условного закона
распределения случайной величины при условии, что
при условии, что :
:
 ;
;
 ;
;
|
|
|
|
|
|
|
|
|
|
|
|
Для
вероятностей в последней таблице также
выполняется условие
нормировки: .
.
Рассмотрим
теперь непрерывный случайный вектор
 .
Так как в этом случае
.
Так как в этом случае при любом
при любом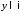 ,
то определение (3.12) условной функции
распределения
,
то определение (3.12) условной функции
распределения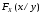 случайной величины
случайной величины при условии, что
при условии, что ,
неприменимо. Для непрерывных случайных
величин
,
неприменимо. Для непрерывных случайных
величин и
и условную функцию распределения
условную функцию распределения определяют следующим образом:
определяют следующим образом: .
.
Вероятность,
стоящая под знаком
предела, представляет собой
вероятность попадания непрерывного
случайного
вектора
 в полосу.
в полосу.
В
соответствии с определением условной
вероятности и свойствами двумерной
функции распределения имеем:
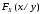


 .
.
Если последний предел существует, то он равен
 .
.
Учитывая,
что у непрерывного случайного вектора
 существует плотность вероятностей
существует плотность вероятностей и
и ,
а также, что у случайной величины
,
а также, что у случайной величины существует плотность вероятностей
существует плотность вероятностей и
и ,
для условной функции распределения
,
для условной функции распределения получаем выражение:
получаем выражение:
 (3.13)
(3.13)
в
точках непрерывности функций
 и
и .
.
Условная
плотность вероятностей
 случайной величины
случайной величины при условии, что
при условии, что ,
по аналогии с одномерным случаем
определяется как производная пох
от условной функции распределения
,
по аналогии с одномерным случаем
определяется как производная пох
от условной функции распределения
 :
:

в
точках, где условная плотность вероятностей
 непрерывна.
непрерывна.
Из (3.13) следует, что
 (3.14)
(3.14)
(при
этом полагается, что
 ,
если
,
если ).
).
Аналогичные
выражения имеют место для условной
функции распределения
 и условной плотности вероятностей
и условной плотности вероятностей случайной величины
случайной величины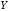 при условии, что
при условии, что :
:
 ;
(3.15)
;
(3.15)

в
точках, где условная плотность вероятностей
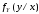 непрерывна;
непрерывна;
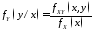 (3.16)
(3.16)
(при
этом полагается, что
 ,
если
,
если ).
).
Как и любая плотность вероятностей, условные плотности вероятностей обладают свойствами:
при фиксированном y
 ;
;  (условие нормировки);
(условие нормировки);
при фиксированном х
 ;
;  (условие нормировки).
(условие нормировки).
Формулы (3.14) и (3.16) дают выражения для условных плотностей вероятностей через безусловные и их также можно записать в виде:

Полученная формула называется правилом умножения плотностей вероятностей, которая является обобщением известного правила умножения вероятностей.
Для непрерывных случайных величин в терминах плотностей вероятностей имеют место также аналоги формулы полной вероятности и формулы Байеса:
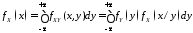 ;
;
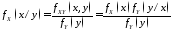
(в
последней формуле
 - априорная плотность вероятностей, а
- априорная плотность вероятностей, а - апостериорная плотность вероятностей).
- апостериорная плотность вероятностей).
Используя понятие условного закона распределения, получаем еще одно эквивалентное определение независимости случайных величин.
Для
независимости случайных величин
 и
и необходимо и достаточно, чтобы условные
законы распределения одной из случайных
величин относительно другой совпадали
с безусловными (аналог равенств
необходимо и достаточно, чтобы условные
законы распределения одной из случайных
величин относительно другой совпадали
с безусловными (аналог равенств ):
):
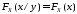 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
 .
.
Кратко о многомерном случае. Здесь возникает дополнительная возможность рассмотрения условных законов распределения одной группы координат случайного вектора относительно другой. Но при этом определения полностью аналогичны.
Так,
например, условная плотность вероятностей
«отрезка»
 вектора
вектора при условии, что случайные величины
при условии, что случайные величины приняли определенные значения
приняли определенные значения ,
задается формулой:
,
задается формулой:
 .
.
Условные числовые характеристики (математическое ожидание и дисперсия) определяются и находятся также, как и безусловные, только в формулах для их вычисления следует безусловные законы распределения заменить на условные.
Если
 - дискретный случайный вектор, то условным
математическим ожиданием случайной
величины
- дискретный случайный вектор, то условным
математическим ожиданием случайной
величины при условии, что
при условии, что ,
называется величина
,
называется величина
а
условным математическим ожиданием
случайной величины
 при условии, что
при условии, что ,
- величина
,
- величина

Если
 - непрерывный случайный вектор, то
условные математические ожидания
случайной величины
- непрерывный случайный вектор, то
условные математические ожидания
случайной величины при условии, что
при условии, что ,
и случайной величины
,
и случайной величины при условии, что
при условии, что ,
определяются формулами:
,
определяются формулами: ;
; .
.
Аналогичные формулы имеют место и для условных дисперсий.
Если
 - дискретный случайный вектор, то
- дискретный случайный вектор, то
 ;
;
 .
.
Если
 - непрерывный случайный вектор, то
- непрерывный случайный вектор, то
 ;
;
 .
.
Отметим,
что, если безусловные математические
ожидания и дисперсия являются числами,
то условные математические ожидания и
дисперсии являются функциями
условия.
Функцию
 называют также функцией регрессии
называют также функцией регрессии на
на ,
а функцию
,
а функцию - функцией регрессии
- функцией регрессии на
на .
.