
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
Метод максимального правдоподобия.
Пусть
![]() - выборка из генеральной совокупности,
имеющей функцию распределения
- выборка из генеральной совокупности,
имеющей функцию распределения![]() ,
зависящую от неизвестного скалярного
параметра
,
зависящую от неизвестного скалярного
параметра![]() .
.
Если закон
распределения наблюдаемой случайной
величины
![]() является непрерывным, т.е. существует
плотность вероятностей
является непрерывным, т.е. существует
плотность вероятностей![]() ,
то функция
,
то функция![]() ,
рассматриваемая при фиксированной
выборке
,
рассматриваемая при фиксированной
выборке![]() как функция параметра
как функция параметра![]() ,
называетсяфункцией правдоподобия.
,
называетсяфункцией правдоподобия.
Если наблюдаемая
случайная величина
![]() имеет дискретный закон распределения,
задаваемый вероятностями
имеет дискретный закон распределения,
задаваемый вероятностями![]() ,
то функция правдоподобия определяется
равенством:
,
то функция правдоподобия определяется
равенством:
![]() .
.
Оценкой
максимального правдоподобия![]() параметра
параметра![]() называется такое значение параметра,
при котором функция правдоподобия при
заданной выборке
называется такое значение параметра,
при котором функция правдоподобия при
заданной выборке![]() достигает максимума:
достигает максимума:
![]()
Если функция
правдоподобия дифференцируема по
![]() ,
то оценку максимального правдоподобия
,
то оценку максимального правдоподобия![]() можно найти, решив относительно
можно найти, решив относительно![]() уравнение правдоподобия
уравнение правдоподобия или равносильное уравнение
или равносильное уравнение .
.
Если
![]() - векторный параметр, то для отыскания
оценки максимального правдоподобия
- векторный параметр, то для отыскания
оценки максимального правдоподобия![]() следует решитьсистему уравнений
правдоподобия
следует решитьсистему уравнений
правдоподобия

Все
изложенные результаты остаются в силе
и при оценивании не самого параметра
![]() ,
а некоторой параметрической функции
,
а некоторой параметрической функции![]() .
.
Оценки максимального правдоподобия являются:
- состоятельными;
- асимптотически эффективными;
- несмещенными не всегда;
- асимптотически нормальными, т.е. при соответствующей нормировке закон распределения оценки максимального правдоподобия является нормальным (что очень важно для нахождения вероятностей отклонения их от истинных значений параметров).
Однако уравнения (системы уравнений) для нахождения оценок максимального правдоподобия могут решаться довольно сложно.
48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
На практике
ограничиться нахождением «хороших»
точечных оценок бывает обычно недостаточно.
Приближенное равенство
![]() лишь указывает на то, что вместо
неизвестного параметра
лишь указывает на то, что вместо
неизвестного параметра![]() можно использовать известное значение
оценки
можно использовать известное значение
оценки![]() .
Однако важно знать (хотя бы в вероятностном
смысле) величину совершаемой при этом
ошибки. Для этого прибегают к построению
интервальных оценок неизвестных
параметров.
.
Однако важно знать (хотя бы в вероятностном
смысле) величину совершаемой при этом
ошибки. Для этого прибегают к построению
интервальных оценок неизвестных
параметров.
Пусть наблюдаемая
величина
![]() имеет функцию распределения
имеет функцию распределения![]() ,
зависящую от неизвестного параметра
,
зависящую от неизвестного параметра![]() .
При интервальном оценивании параметра
.
При интервальном оценивании параметра![]() ищут две такие статистики
ищут две такие статистики![]() и
и![]() (
(![]() и
и![]() - случайные величины!), для которых при
заданном
- случайные величины!), для которых при
заданном![]() выполняется соотношение
выполняется соотношение![]() .
В этом случае интервал
.
В этом случае интервал![]() называют
называют![]() -доверительньм
интервалом для параметра
-доверительньм
интервалом для параметра![]() ,
число
,
число![]() -доверительной вероятностью(надежностью, коэффициентом доверия),
-доверительной вероятностью(надежностью, коэффициентом доверия),![]() и
и![]() - нижней и верхнейдоверительными
границамисоответственно.
- нижней и верхнейдоверительными
границамисоответственно.
Таким образом,
![]() -доверительный
интервал — этослучайный интервал,
зависящий от выборки (но не от
-доверительный
интервал — этослучайный интервал,
зависящий от выборки (но не от![]() ),
который содержит (накрывает) истинное
значение неизвестного параметра
),
который содержит (накрывает) истинное
значение неизвестного параметра![]() с вероятностью
с вероятностью![]() .
На практике обычно используют значения
доверительной вероятности
.
На практике обычно используют значения
доверительной вероятности![]() из небольшого набора близких к 1 значений
(0,9; 0,95; 0,98; 0,99 и т. д.) и строят соответствующие
им доверительные интервалы. Построение
доверительных интервалов для отдельных
параметров распределения генеральной
совокупности зависит как от вида закона
распределения, так и от того, являются
известными значения остальных параметров
распределения или нет.
из небольшого набора близких к 1 значений
(0,9; 0,95; 0,98; 0,99 и т. д.) и строят соответствующие
им доверительные интервалы. Построение
доверительных интервалов для отдельных
параметров распределения генеральной
совокупности зависит как от вида закона
распределения, так и от того, являются
известными значения остальных параметров
распределения или нет.
Если наблюдаемая
случайная величина
![]() имеет нормальный закон распределения
имеет нормальный закон распределения![]() с неизвестным математическим ожиданием
с неизвестным математическим ожиданием![]() иизвестной дисперсией
иизвестной дисперсией![]() ,
тодоверительный интервал для
математического ожидания
,
тодоверительный интервал для
математического ожидания
![]() имеет вид:
имеет вид:
 ,
,
где
![]() - выборочное среднее;
- выборочное среднее;![]() - объем выборки; число
- объем выборки; число![]() - такое значение аргумента функции
Лапласа
- такое значение аргумента функции
Лапласа при котором
при котором![]() .
Находят число
.
Находят число![]() по заданной доверительной вероятности
по заданной доверительной вероятности![]() из табл. П2.
из табл. П2.
Квантилью,
соответствующей вероятности![]() ,
называется такое значение
,
называется такое значение![]() ,
при котором выполняется соотношение
,
при котором выполняется соотношение ,
где
,
где![]() – плотность вероятностей соответствующего
закона распределения (слово квантиль
– женского рода). Геометрическое
пояснение смысла квантили, отвечающей
вероятности
– плотность вероятностей соответствующего
закона распределения (слово квантиль
– женского рода). Геометрическое
пояснение смысла квантили, отвечающей
вероятности![]() ,
приведено на рис. 2.
,
приведено на рис. 2.

Рис. 2.
Геометрическое пояснение смысла квантили
![]() ,
отвечающей вероятности
,
отвечающей вероятности![]()
В этой терминологии
число
![]() есть (1+)/2 - квантиль
стандартного нормальногоN(0,1)
закона распределения.
есть (1+)/2 - квантиль
стандартного нормальногоN(0,1)
закона распределения.
Если
наблюдаемая случайная величина
![]() имеет нормальный закон распределения
имеет нормальный закон распределения![]() с неизвестным математическим ожиданием
с неизвестным математическим ожиданием![]() инеизвестнойдисперсией
инеизвестнойдисперсией![]() ,
тодоверительный интервал для
математического ожидания
,
тодоверительный интервал для
математического ожидания
![]() имеет вид:
имеет вид:
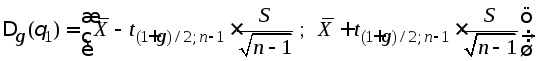
где
![]() - выборочная дисперсия,
- выборочная дисперсия,![]() ,
,![]() - объем выборки, число
- объем выборки, число![]() –
–![]() - квантиль распределения Стьюдента
- квантиль распределения Стьюдента![]() с (n—1) степенью
свободы. Находят квантиль
с (n—1) степенью
свободы. Находят квантиль![]() по заданным
по заданным![]() и
и![]() из табл. ПЗ.
из табл. ПЗ.
При больших
![]() (практически при
(практически при![]() )
распределение Стьюдента приближается
(в смысле слабой сходимости) к стандартному
нормальному закону распределения,
поэтому в этом случае
)
распределение Стьюдента приближается
(в смысле слабой сходимости) к стандартному
нормальному закону распределения,
поэтому в этом случае![]() .
.
