
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
25. Теоремы о числовых характеристиках.
Теорема 1 (теорема сложения математических ожиданий).
Математическое
ожидание суммы двух любых
случайных величин
 и
и равно сумме их математических ожиданий:
равно сумме их математических ожиданий: .
.
▲ Докажем теорему в непрерывном случае, в дискретном случае доказать самостоятельно.
Из обобщения ОТМО на двумерный случай
при
 имеем:
имеем:

 ■.
■.
По индукции теорема 1 обобщается на сумму любого конечного числа случайных величин:
 .
.
Теорема 2 (теорема умножения математических ожиданий).
Математическое
ожидание произведения двух независимых
случайных величин
 и
и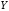 равно
произведению их математических ожиданий:
равно
произведению их математических ожиданий: .
.
▲ Докажем теорему в непрерывном случае, в дискретном случае доказать самостоятельно.
Если
непрерывные случайные величины
 и
и являются независимыми, то
являются независимыми, то .
Поэтому из обобщения ОТМО на двумерный
случай при
.
Поэтому из обобщения ОТМО на двумерный
случай при имеем:
имеем:
 ■.
■.
По
индукции теорема 2 обобщается на
произведение любого конечного числа
независимых (в совокупности) случайных
величин:
 .
.
26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
Определение.
Случайные величины
 и
и ,
для которых корреляционный момент
,
для которых корреляционный момент ,
называютсянекоррелированными.
,
называютсянекоррелированными.
Учитывая,
что
 ,
,
получаем:
случайные величины
 и
и являются некоррелированными тогда и
только тогда, когда
являются некоррелированными тогда и
только тогда, когда .
.
Отсюда
и из теоремы 2 вытекает, что из независимости
случайных величин всегда
следует их некоррелированность. Обратное,
вообще говоря, неверно. Можно только
сказать, что если случайные величины
являются коррелированными, так, что
 ,
то они являются зависимыми.
,
то они являются зависимыми.
Пример.
Равномерное
распределение в круге
 .
.

Ранее
были найдены одномерные плотности
вероятностей координат вектора
 :
:


и
установлено, что случайные величины
 и
и являются зависимыми, так как
являются зависимыми, так как .
.
Найдем
корреляционный момент
 СВ
СВ и
и .
.

в силу нечетности подинтегральной функции и симметричности относительно нуля пределов интегрирования.
По
аналогичным соображениям
 Найдем
Найдем .
.

также в силу нечетности подинтегральной функции.
Таким
образом,
 и, следовательно, случайные величины
и, следовательно, случайные величины и
и являются зависимыми, но некоррелированными.
являются зависимыми, но некоррелированными.
Понятие некоррелированности случайных величин играет важную роль в теории вероятностей. Подтверждением тому является следующая теорема.
Теорема 3 (теорема сложения дисперсий).
Для
любых действительных чисел
 и любых случайных величин
и любых случайных величин и
и ,
имеющих конечную дисперсию
,
имеющих конечную дисперсию .
.
В
частности, если
 и случайные величины
и случайные величины и
и являются некоррелированными, то имеет
место свойство аддитивности дисперсии:
являются некоррелированными, то имеет
место свойство аддитивности дисперсии: .
.
▲ Доказательство
теоремы основано только на свойствах
математического ожидания и определении
корреляционного момента
 :
:


 .■.
.■.
По индукции утверждение теоремы 3 обобщается на линейную комбинацию любого конечного числа случайных величин следующим образом.
Для
любых действительных чисел
 и случайных величин
и случайных величин ,
имеющих конечную дисперсию
,
имеющих конечную дисперсию
 .
.
В
частности, если все
 ,
а случайные величины
,
а случайные величины являются попарно некоррелированными
(
являются попарно некоррелированными
( ),
то имеет место свойство аддитивности
дисперсии:
),
то имеет место свойство аддитивности
дисперсии: .
.
27. Коэффициент корреляции, его свойства и вероятностный смысл.
Значение
корреляционного момента
 зависит от единиц измерения случайных
величин
зависит от единиц измерения случайных
величин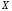 и
и .
Безразмерным аналогом
.
Безразмерным аналогом являетсякоэффициент
корреляции,
определяемый формулой:
являетсякоэффициент
корреляции,
определяемый формулой:
 ,
,
где
 - средние квадратические отклонения
случайных величин
- средние квадратические отклонения
случайных величин и
и .
.
Свойства коэффициента корреляции.
 ,
если случайные величины
,
если случайные величины
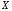 и
и являются независимыми.
являются независимыми.
(Свойство
очевидно, так как в этом случае
 ).
).
Коэффициент корреляции по модулю не превосходит 1:
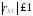 .
.
▲ В
соответствии со свойством 1 дисперсии
 .
.
Положим
 .
Тогда
.
Тогда ,
,
Откуда
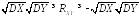 .
.
Следовательно,
 ,
и поэтому
,
и поэтому .■.
.■.
 тогда
и только тогда, когда случайные величины
тогда
и только тогда, когда случайные величины
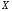 и
и связаны линейной зависимостью, то есть
существуют действительные числаА
и В
такие, что
связаны линейной зависимостью, то есть
существуют действительные числаА
и В
такие, что
 .
.
▲ Необходимость.
Предположим, что
 .
Тогда
.
Тогда и из доказательства свойства 2 следует,
что
и из доказательства свойства 2 следует,
что при
при .
В соответствии со свойством 1 дисперсии
это означает, что
.
В соответствии со свойством 1 дисперсии
это означает, что ,
откуда
,
откуда и значит
и значит .
.
Достаточность.
Пусть
 .
Тогда
.
Тогда ,
а корреляционный момент случайных
величин
,
а корреляционный момент случайных
величин и
и равен
равен

 .
.
Поэтому  ■.
■.
Итак,
 для независимых случайных величин и
достигает максимального по модулю
значения
для независимых случайных величин и
достигает максимального по модулю
значения для сильно (линейно) зависимых случайных
величин. Поэтому значение коэффициента
корреляции можно интерпретировать как
степень линейной зависимости между
случайными величинами.
для сильно (линейно) зависимых случайных
величин. Поэтому значение коэффициента
корреляции можно интерпретировать как
степень линейной зависимости между
случайными величинами.
Геометрическая
иллюстрация: чем больше по модулю
 ,
тем плотнее значения случайного вектора
,
тем плотнее значения случайного вектора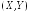 располагаются вдоль некоторой прямой.
Многомерный случай.
располагаются вдоль некоторой прямой.
Многомерный случай.
Основными
числовыми характеристики
 -мерного
случайного вектора
-мерного
случайного вектора являются:
являются:
математическое ожидание
 ;
;корреляционная матрица
 ,
элементами которой являются всевозможные
попарные корреляционные моменты
координат:
,
элементами которой являются всевозможные
попарные корреляционные моменты
координат: .
.
Свойства корреляционной матрицы.
Матрица
 является симметрической размера
является симметрической размера :
: ,
, .
.На диагонали матрицы
 расположены дисперсии координат
случайного вектора
расположены дисперсии координат
случайного вектора :
: ,
, .
.Матрица
 является неотрицательно определенной
матрицей, то есть для любого
является неотрицательно определенной
матрицей, то есть для любого и для любых действительных чисел
и для любых действительных чисел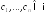
 .
.
▲ Обозначим
 - центрированную случайную величины,
- центрированную случайную величины,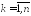 .
Тогда
.
Тогда и для произвольных чисел
и для произвольных чисел имеем:
имеем:

 ■.
■.
Наряду
с корреляционной матрицей
 ,
иногда рассматривают нормированную
корреляционную матрицу
,
иногда рассматривают нормированную
корреляционную матрицу ,
элементами которой являются всевозможные
попарные коэффициенты корреляции
координат:
,
элементами которой являются всевозможные
попарные коэффициенты корреляции
координат: .
Отличие ее от просто корреляционной
матрицы состоит в том, что у нормированной
корреляционной матрицы все диагональные
элементы равны 1:
.
Отличие ее от просто корреляционной
матрицы состоит в том, что у нормированной
корреляционной матрицы все диагональные
элементы равны 1: .
.
