
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
 -алгебра
событий
-алгебра
событий
Определение. Пустьпроизвольное
множество. Класс подмножеств множества(не обязательно всех) называется
подмножеств множества(не обязательно всех) называется -алгеброй
событий или
-алгеброй
событий или -алгеброй
подмножеств, если
выполнены следующие свойства:
-алгеброй
подмножеств, если
выполнены следующие свойства:
А1)
 (
( -алгебра
событий содержит достоверное событие);
-алгебра
событий содержит достоверное событие);
А2) если
 ,
то
,
то (вместе с любым событием
(вместе с любым событием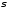 -алгебра
содержит противоположное событие);
-алгебра
содержит противоположное событие);
А3) если
 ,
то
,
то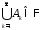 (вместе с любым конечным или счетным
набором событий
(вместе с любым конечным или счетным
набором событий -алгебра
содержит их сумму).
-алгебра
содержит их сумму).
Свойства А1) – А3) часто называют аксиомами
 -алгебры.
-алгебры.
Проверим, что этого набора аксиом
достаточно для замкнутости класса
подмножеств
 и относительно других операций над
событиями.
и относительно других операций над
событиями.
1.
 (
( -алгебра
событий содержит невозможное событие).
-алгебра
событий содержит невозможное событие).
2. При выполнении А1) и А2) свойство А3) эквивалентно свойству А4):
А4) если
 ,
то
,
то
 (вместе с любым конечным или счетным
набором событий
(вместе с любым конечным или счетным
набором событий
 -алгебра
содержит их произведение).
-алгебра
содержит их произведение).
3. Если
 ,
то
,
то
 .
.
Пример. Пусть
 -
конечное пространство элементарных
событий. Следующие классы подмножеств
-
конечное пространство элементарных
событий. Следующие классы подмножеств являются
являются -алгебрами:
-алгебрами:
1.
 -
тривиальная
-
тривиальная -алгебра.
-алгебра.
2.
 ,
где А – произвольное подмножество
,
где А – произвольное подмножество .
.
3.
 - множество всех подмножеств
- множество всех подмножеств (доказать, что при этом число всех
подмножеств в
(доказать, что при этом число всех
подмножеств в равно
равно ).
).
Определим теперь вероятность как
функцию, определенную на множестве
событий (то есть функцию, которая каждому
событию ставит в соответствие число),
а точнее как неотрицательную нормированную
меру, заданную на
 -алгебре
событий
-алгебре
событий .
.
Вероятность как нормированная мера
Определение. Пара ,
в которой
,
в которой - некоторое множество, а
- некоторое множество, а -
- -алгебра
его подмножеств называетсяизмеримым
пространством.
-алгебра
его подмножеств называетсяизмеримым
пространством.
Определение. Пусть - некоторое множество,
- некоторое множество, -
- -алгебра
его подмножеств. Функция
-алгебра
его подмножеств. Функция называетсямеройна измеримом
пространстве
называетсямеройна измеримом
пространстве ,
если она удовлетворяет условиям:
,
если она удовлетворяет условиям:
М1) Для любого множества
 его мера неотрицательна:
его мера неотрицательна: .
.
М2) Для любого счетного набора попарно
непересекающихся множеств
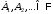 (то есть такого, что
(то есть такого, что )
мера их объединения равна сумме их мер:
)
мера их объединения равна сумме их мер: (счетная аддитивностьили
(счетная аддитивностьили -аддитивность).
-аддитивность).
Другими словами, мера есть неотрицательная счетно-аддитивная функция множеств.
Определение.Пусть - некоторое множество и
- некоторое множество и -
- -алгебра
его подмножеств. Мера
-алгебра
его подмножеств. Мера называетсянормированной, если
называетсянормированной, если .
.
Определение.Пусть - произвольное пространство элементарных
событий и
- произвольное пространство элементарных
событий и -
- -алгебра
его подмножеств (событий). Вероятностью
или вероятностной мерой на
-алгебра
его подмножеств (событий). Вероятностью
или вероятностной мерой на называется функция
называется функция ,
удовлетворяющая следующим аксиомам:
,
удовлетворяющая следующим аксиомам:
Р1). Аксиома неотрицательности:
Для любого события
 выполняется
неравенство:
выполняется
неравенство: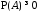 ;
;
Р2). Аксиома нормированности:
Вероятность достоверного события равна
единице:
 .
.
Р3). Аксиома счетной аддитивности:
Для любой счетного набора попарно
несовместных событий

 имеет место равенство:
имеет место равенство: .
.
Определение. Тройка ,
в которой
,
в которой - пространство элементарных событий,
- пространство элементарных событий, -
- -алгебра
событий и
-алгебра
событий и - вероятностная мера на
- вероятностная мера на называетсявероятностным пространством.
называетсявероятностным пространством.
Теорема(доказательство см. Б.В. Гнеденко, Курс теории вероятностей).
Аксиома счетной аддитивности Р3) эквивалентна выполнению следующих двух аксиом Р3*) и Р4):
Р3*).Аксиома конечной аддитивности:
Для любого конечного набора событий
 ,
являющихся попарно несовместными
,
являющихся попарно несовместными ,
имеет место равенство:
,
имеет место равенство: .
.
Р4). Аксиома непрерывности:
Если события
 обладают свойствами:
обладают свойствами:
 ;
; ,
,
(при этом говорят, что события образуют
убывающую последовательность), то
 .
.
Из аксиоматического определения вероятности вытекают следующие свойства вероятности (здесь и везде в дальнейшем под знаком вероятности появляются только события!).
1°.
 .
.
2°.
 .
.
3°.
 .
.
4°.
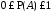 .
.
(Свойства 1 – 4 были доказаны при рассмотрении классического определения вероятности сразу в общем случае).
5°. Теорема сложения вероятностей.
Для любых событий
 (не обязательно несовместных)
(не обязательно несовместных)
 .
.
▲ Представим событие Вв виде:
 .
.
Поскольку события
 являются несовместными, то по аксиоме
аддитивности Р3)
являются несовместными, то по аксиоме
аддитивности Р3)
 .
(1)
.
(1)
Представим событие
 в виде:
в виде:
 .
.
Поскольку события
 являются несовместными, то по аксиоме
Р3)
являются несовместными, то по аксиоме
Р3)
 .
(2)
.
(2)
Вычитая из равенства (2) равенство (1), получаем
 .
■
.
■
6°. Если события
 образуют полную группу событий, то
образуют полную группу событий, то
 .
.
▲ Свойство следует из определения полной группы событий и аксиом Р2) и Р3). ■
7°.
 .
.
▲ Представим событие Ав виде:
 .
.
Поскольку события
 являются несовместными, то по аксиоме
аддитивности Р3)
являются несовместными, то по аксиоме
аддитивности Р3)
 .
■
.
■
