
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
Характеристические функции случайных векторов
Характеристической
функцией случайного вектора
 называется комплекснозначная функция
называется комплекснозначная функция вещественных переменных, определяемая
для любого
вещественных переменных, определяемая
для любого равенством:
равенством:
или
в векторной форме
 ,
,
где
 означает скалярное произведение
векторов.
означает скалярное произведение
векторов.
Характеристическая функция случайного вектора обладает всеми свойствами (с очевидными изменениями в формулировках) одномерной характеристической функции. Но есть и дополнительные полезные свойства.
 По
характеристической функции
По
характеристической функции
 случайного вектора
случайного вектора можно найти характеристическую функцию
любой группы из
можно найти характеристическую функцию
любой группы из его координат
его координат .
Для этого следует положить аргументы
.
Для этого следует положить аргументы при
при .
.
Так,
например, характеристическая функция
«отрезка»
 случайного вектора
случайного вектора равна
равна ,
,
а
характеристическая функция любой
координаты
 вектора
вектора равна
равна
 .
.
 Если
Если
 - характеристическая функция случайного
вектора
- характеристическая функция случайного
вектора ,
то характеристическая функция суммы
его координат
,
то характеристическая функция суммы
его координат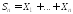 равна
равна ,
,
то
есть следует положить все
 .
.
Задача
1. Найти
характеристическую функцию двумерного
нормального случайного вектора
 .
.
Ответ:
 .
.
Задача
2. Найти
характеристическую функцию суммы
 двумерного
нормального случайного вектора
двумерного
нормального случайного вектора
 и по ней определить закон распределения
случайной величины
и по ней определить закон распределения
случайной величины .
.
Ответ:
 .
.
Задача
3. Найти
характеристическую функцию многомерного
нормального случайного вектора
 .
.
Ответ:
 .
.
36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
Ранее были введены три вида сходимости последовательностей случайных величин: по вероятности, почти наверное и в среднем. Еще один вид сходимости основан на близости законов распределения случайных величин, то есть на сходимости последовательности их функций распределения.
Пусть
заданы последовательность случайных
величин
 ,
имеющих функции распределения
,
имеющих функции распределения ,
и случайная величина
,
и случайная величина с функцией распределения
с функцией распределения .
Было бы естественно считать, что, если
случайная величина
.
Было бы естественно считать, что, если
случайная величина ,
то ее закон распределения сходится при
,
то ее закон распределения сходится при к закону распределения случайной
величины
к закону распределения случайной
величины .
Однако, требовать при этом равномерную
сходимость
.
Однако, требовать при этом равномерную
сходимость к
к (то есть, чтобы
(то есть, чтобы )
в общем случае неразумно, поскольку она
никогда не будет иметь места, если
функция распределения случайной величины
)
в общем случае неразумно, поскольку она
никогда не будет иметь места, если
функция распределения случайной величины имеет хотя бы один разрыв. Поэтому
сходимость последовательности функций
распределения
имеет хотя бы один разрыв. Поэтому
сходимость последовательности функций
распределения к функции распределения
к функции распределения понимают в смысле следующего определения.
понимают в смысле следующего определения.
Определение.
Говорят, что последовательность функций
распределения
 слабо сходится
к функции распределения
слабо сходится
к функции распределения
 и обозначают
и обозначают ,
если
,
если
в
каждой точке
 ,
где предельная функция распределения
,
где предельная функция распределения является непрерывной.
является непрерывной.
При
этом также говорят, что последовательность
случайных величин
 слабо
(или по
распределению)
сходится
к случайной величине
слабо
(или по
распределению)
сходится
к случайной величине
 и записывают
и записывают (или
(или )
или, что последовательность случайных
величин
)
или, что последовательность случайных
величин слабо сходится
к распределению
слабо сходится
к распределению
 и обозначают
и обозначают .
.
Смысл слабой сходимости: это поточечная сходимость функций распределения во всех точках непрерывности предельной функции распределения.
Выделим
важный частный случай, когда предельная
функция распределения
 является непрерывной для любого
является непрерывной для любого .
При этом
.
При этом ,
если
,
если для любого
для любого и, более того, в силу монотонности и
ограниченности функций распределения
сходимость являетсяравномерной
по
и, более того, в силу монотонности и
ограниченности функций распределения
сходимость являетсяравномерной
по
 :
: (подробнее см. учебник Чистякова В.П.
«Курс теории вероятностей»).
(подробнее см. учебник Чистякова В.П.
«Курс теории вероятностей»).
Замечание.
Отметим, что запись
 не совсем корректна: если предельную
случайную величину
не совсем корректна: если предельную
случайную величину заменить на любую другую случайную
величину
заменить на любую другую случайную
величину с тем же законом распределения, то ничего
не изменится, в том же смысле и
с тем же законом распределения, то ничего
не изменится, в том же смысле и .
Поэтому слабая сходимость все же не
есть сходимость последовательности
случайных величин и ей нельзя пользоваться
как сходимостями по вероятности, почти
наверное и в среднем, для которых
предельная случайная величина единственна
(хотя бы с точностью до значений на
множестве нулевой вероятности). По этой
причине слабая сходимость и рассматривается
отдельно.
.
Поэтому слабая сходимость все же не
есть сходимость последовательности
случайных величин и ей нельзя пользоваться
как сходимостями по вероятности, почти
наверное и в среднем, для которых
предельная случайная величина единственна
(хотя бы с точностью до значений на
множестве нулевой вероятности). По этой
причине слабая сходимость и рассматривается
отдельно.
Следующее утверждение устанавливает соотношение между слабой сходимостью и сходимостью по вероятности.
Лемма.
1.
Из сходимости по вероятности следует
слабая сходимость: если
 ,
то
,
то .
.
2.
Если предельное распределение является
вырожденным, то сходимость по вероятности
и слабая сходимость эквивалентны: если
 ,
то
,
то .
.
▲ 1.
Пусть
 - точка непрерывности функции распределения
- точка непрерывности функции распределения .
Требуется доказать, что тогда
.
Требуется доказать, что тогда .
Зафиксируем
.
Зафиксируем такое, что
такое, что непрерывна в точках
непрерывна в точках .
.
Функцию
распределения
 можно записать в виде:
можно записать в виде:
 .
.
Оценим
вероятность
 сверху и снизу. Для вероятности
сверху и снизу. Для вероятности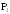 имеем:
имеем:

и
вероятность справа может быть выбором
 сделана сколь угодно малой, поскольку
сделана сколь угодно малой, поскольку .
.
Для
вероятности
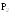 ,
с одной стороны,
,
с одной стороны,

(так
как, если
 ,
то тем более
,
то тем более ).
).
С
другой стороны,
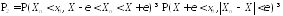

(здесь
первое неравенство очевидно, а второе
следует из того, что
 ).
).
Таким
образом, получаем для
 следующее двойное неравенство:
следующее двойное неравенство:
 .
.
Устремляя
теперь
 ,
получаем
,
получаем ,
,
а
предельный переход при
 с учетом того, что
с учетом того, что - точка непрерывности
- точка непрерывности ,
дает
,
дает .
.
2.
Пусть
 для любого
для любого ,
являющегося точкой непрерывности
предельной функции распределения
,
являющегося точкой непрерывности
предельной функции распределения ,
то есть при всех
,
то есть при всех .
.
Докажем,
что при этом
 для любого
для любого .
.
Раскроем модуль под знаком вероятности и выполним ряд преобразований:

 ,
,
поскольку
в точках
 и
и функция распределения
функция распределения непрерывна. Окончательно, сходимость
непрерывна. Окончательно, сходимость следует из леммы о двух милиционерах
■.
следует из леммы о двух милиционерах
■.
Замечательный факт состоит в том, что слабая сходимость распределений полностью характеризуется с помощью характеристических функций.
 Теорема
непрерывности
(без доказательства).
Теорема
непрерывности
(без доказательства).
Пусть
 - последовательность характеристических
функций, а
- последовательность характеристических
функций, а - последовательность соответствующих
функций распределений. Для слабой
сходимости
- последовательность соответствующих
функций распределений. Для слабой
сходимости необходимо и достаточно, чтобы
необходимо и достаточно, чтобы для любого
для любого ,
где
,
где - характеристическая функция,
соответствующая предельной функции
распределения
- характеристическая функция,
соответствующая предельной функции
распределения .
.
Теорема непрерывности устанавливает, что соответствие между функциями распределения и характеристическими функциями является не только взаимнооднозначным (в соответствии с теоремой единственности), но и непрерывным в том смысле, что пределу в классе функций распределения относительно слабой сходимости соответствует предел в классе характеристических функций относительно поточечной сходимости.
Теорема непрерывности является основным средством доказательства центральных предельных теорем (теорем о слабой сходимости распределений на числовой прямой).
