- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
29. Функции от св и их законы распределения. Функции случайных аргументов
Пусть
 - случайный вектор, закон распределения
которого известен, и
- случайный вектор, закон распределения
которого известен, и - скалярная (для простоты) неслучайная
функция, область определения которой
содержит множество возможных значений
вектора
- скалярная (для простоты) неслучайная
функция, область определения которой
содержит множество возможных значений
вектора .
Рассмотрим случайную величину
.
Рассмотрим случайную величину (для того, чтобы функция случайных
аргументов
(для того, чтобы функция случайных
аргументов являлась случайной величиной, функция
являлась случайной величиной, функция должна быть борелевской, см. раздел
«Основная теорема о математическом
ожидании»). Известно, что для нахождения
числовых характеристик случайной
величины
должна быть борелевской, см. раздел
«Основная теорема о математическом
ожидании»). Известно, что для нахождения
числовых характеристик случайной
величины достаточно знать только закон распределения
случайного вектора
достаточно знать только закон распределения
случайного вектора .
Однако, во многих приложениях, особенно
в математической статистике, необходимо
уметь находить в явном виде закон
распределения случайной величиныY,
являющейся функцией случайных аргументов.
Рассмотрим вначале задачу нахождения
закона распределения случайной величины
Y
в одномерном случае (
.
Однако, во многих приложениях, особенно
в математической статистике, необходимо
уметь находить в явном виде закон
распределения случайной величиныY,
являющейся функцией случайных аргументов.
Рассмотрим вначале задачу нахождения
закона распределения случайной величины
Y
в одномерном случае ( ).
).
Функции от случайных величин
Дискретный
случай. Пусть
 – дискретная случайная величина,
принимающая значения
– дискретная случайная величина,
принимающая значения с вероятностями
с вероятностями (случай счетного числа значений случайной
величины
(случай счетного числа значений случайной
величины рассмотреть самостоятельно). Тогда для
произвольной неслучайной функции
рассмотреть самостоятельно). Тогда для
произвольной неслучайной функции ,
область определения которой содержит
множество возможных значений случайной
величины
,
область определения которой содержит
множество возможных значений случайной
величины ,
случайная величина
,
случайная величина является дискретной и задача состоит
в нахождении ее закона распределения.
является дискретной и задача состоит
в нахождении ее закона распределения.

а)
Предположим вначале, что все значения
 различны (так, в частности, может быть,
если функция
различны (так, в частности, может быть,
если функция является монотонной в области возможных
значений случайной величины
является монотонной в области возможных
значений случайной величины ).
Тогда случайная величина
).
Тогда случайная величина будет иметь столько же возможных значений
будет иметь столько же возможных значений ,
как и случайная величина
,
как и случайная величина ,
с
,
с и при этом
и при этом
 .
(4.1)
.
(4.1)
Таким
образом, закон распределения случайной
величины
 имеет вид:
имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
где
в соответствии с (4.1) вероятности
 .
.
б)
Предположим теперь, что среди значений
 есть совпадающие (это может быть, в
частности, если функция
есть совпадающие (это может быть, в
частности, если функция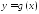 не является монотонной в области
возможных значений случайной величины
не является монотонной в области
возможных значений случайной величины ).
Тогда случайная величина
).
Тогда случайная величина будет иметь меньше возможных значений,
чем случайная величина
будет иметь меньше возможных значений,
чем случайная величина ,
и ими являются
,
и ими являются ,
, ,
различные среди
,
различные среди .
При этом вероятности
.
При этом вероятности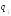 значений
значений определяются по формуле:
определяются по формуле:


 ,
(4.2)
,
(4.2)

Закон
распределения случайной величины
 в данном случае имеет вид:
в данном случае имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
где
в соответствии с (4.2) вероятности
 являются суммой вероятностей
являются суммой вероятностей тех значений
тех значений ,
для которых
,
для которых .
. ,
, .
.
Пример.
Найти закон распределения случайной
величины
 ,
если случайная величинаХ
является дискретной и имеет закон
распределения
,
если случайная величинаХ
является дискретной и имеет закон
распределения
|
|
-2 |
-1 |
0 |
1 |
2 |
|
|
0.2 |
0.2 |
0.2 |
0.2 |
0.2 |
Решение.
В соответствии с (4.2) закон распределения
случайной величины
 имеет вид:
имеет вид:
|
|
0 |
1 |
2 |
|
|
|
0.2 |
0.4 |
0.4 |
|
Непрерывный
случай. Если
 – непрерывная случайная величина с
плотностью вероятностей
– непрерывная случайная величина с
плотностью вероятностей ,
а
,
а – дифференцируемая функция в области
возможных значений случайной величиныХ,
то величина
– дифференцируемая функция в области
возможных значений случайной величиныХ,
то величина
 является непрерывной случайной величиной
и задача состоит в нахождении плотности
вероятностей
является непрерывной случайной величиной
и задача состоит в нахождении плотности
вероятностей .
.
Предположим
вначале, что
 -монотонно
возрастающая
функция в области возможных значений
случайной величины Х.
Тогда у функции
-монотонно
возрастающая
функция в области возможных значений
случайной величины Х.
Тогда у функции
 существует однозначная обратная функция
существует однозначная обратная функция
 и функцию распределения случайной
величины
и функцию распределения случайной
величины можно записать в виде:
можно записать в виде: .
.
Дифференцируя
обе части последнего равенства по
 ,
получаем:
,
получаем: .
(4.3)
.
(4.3)
Для
монотонно
убывающей
в области возможных значений случайной
величины Х
функции

 ,
,
а
после дифференцирования по
 обеих частей этого равенства имеем:
обеих частей этого равенства имеем:
 .
(4.4)
.
(4.4)
Объединяя полученные в (4.3) и (4.4) результаты, получаем:
Если
 – непрерывная случайная величина с
плотностью вероятностей
– непрерывная случайная величина с
плотностью вероятностей ,
а
,
а – монотонная дифференцируемая функция,
то случайная величина
– монотонная дифференцируемая функция,
то случайная величина является непрерывной и ее плотность
вероятностей
является непрерывной и ее плотность
вероятностей определяется через
определяется через по формуле:
по формуле: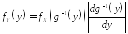 ,
(4.5)
,
(4.5)
где
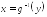 – функция, обратная к функции
– функция, обратная к функции (отметим, что равенство (4.5) имеет место
только в точках непрерывности плотностей
вероятностей
(отметим, что равенство (4.5) имеет место
только в точках непрерывности плотностей
вероятностей и
и ).
).
Если
дифференцируемая функция
 не является
монотонной
в области
не является
монотонной
в области 
возможных
значений случайной величины
 ,
то ее область определения можно разбить
на
,
то ее область определения можно разбить
на непересекающихся интервалов, на каждом
из которых она монотонной будет и будет
иметь однозначную обратную функцию
непересекающихся интервалов, на каждом
из которых она монотонной будет и будет
иметь однозначную обратную функцию .
Применяя формулу (4.5) на каждом интервале
монотонности, получаем:
.
Применяя формулу (4.5) на каждом интервале
монотонности, получаем: .
(4.6)
.
(4.6)
Пример
1. Пусть
 – непрерывная случайная величина с
плотностью вероятностей
– непрерывная случайная величина с
плотностью вероятностей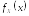 ,
а
,
а .
Найти плотность вероятностей
.
Найти плотность вероятностей .
.
Решение.
В данном случае функция
 является монотонной при любых значениях
является монотонной при любых значениях (при
(при функция
функция возрастает, при
возрастает, при - убывает). Функция, обратная к
- убывает). Функция, обратная к ,
имеет вид:
,
имеет вид: ,
а ее производная
,
а ее производная .
Поэтому в соответствии с (4.5):
.
Поэтому в соответствии с (4.5): .
(4.7)
.
(4.7)
а)
Рассмотрим линейное преобразование
вида
 над случайной величиной
над случайной величиной .
.
В
соответствии с (4.7) в этом случае
 ,
а с учетом того, что
,
а с учетом того, что

для
плотности вероятностей случайной
величины
 имеем выражение:
имеем выражение:

Полученный
результат схематично можно записать в
виде:

и
он означает, что из равномерного
распределения на отрезке
 можно получить равномерное распределение
на любом отрезке
можно получить равномерное распределение
на любом отрезке путем линейного преобразования.
путем линейного преобразования.
б)
Рассмотрим линейное преобразование
вида
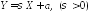 над случайной величиной
над случайной величиной .
.
В
соответствии с (4.7) в этом случае
 ,
а с учетом того, что
,
а с учетом того, что

для
плотности вероятностей случайной
величины
 имеем выражение:
имеем выражение:
 .
.
Полученный результат схематично можно записать в виде:
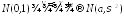
и
он означает, что из стандартного
нормального распределения можно получить
нормальное распределение с любыми
параметрами
 путем линейного преобразования.
путем линейного преобразования.
Пример
2. Пусть
 ,
а
,
а .
Найти плотность вероятностей
.
Найти плотность вероятностей .
.
Решение.
В данном случае функция
 не является монотонной в области
возможных значений случайной величины
не является монотонной в области
возможных значений случайной величины и имеет два интервала монотонности
и имеет два интервала монотонности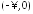 и
и .
На каждом из интервалов функция
.
На каждом из интервалов функция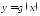 имеет однозначную обратную функцию:
имеет однозначную обратную функцию: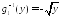 на первом интервале
на первом интервале и
и - на втором
- на втором .
Поскольку модуль производной
.
Поскольку модуль производной ,
, ,
то в соответствии с (4.6):
,
то в соответствии с (4.6): ,
,
а
с учетом того, что
 ,
получаем:
,
получаем:
 ,
,
 при
при
 .
.
Пример
3. Пусть
 - строго монотонная функция распределения,
а случайная величина
- строго монотонная функция распределения,
а случайная величина .
Тогда случайная величина
.
Тогда случайная величина имеет заданную функцию распределения
имеет заданную функцию распределения .
.
Решение.
Действительно,
 .
.
Последнее
равенство следует из того, что функция
распределения случайной величины
 имеет вид:
имеет вид:
 .
.
Смысл
примера 3.
Предположим, что требуется получить
 значений
значений случайной величины
случайной величины с заданным законом распределения
(смоделировать случайную величину
с заданным законом распределения
(смоделировать случайную величину ).
Для этого в соответствии с примером 3
необходимо найти функцию распределения
).
Для этого в соответствии с примером 3
необходимо найти функцию распределения случайной величины
случайной величины и, если она имеет однозначную обратную
функцию, то положить
и, если она имеет однозначную обратную
функцию, то положить
 ,
,
 ,
,
где
 - значения случайной величины, имеющей
равномерное распределение на отрезке
- значения случайной величины, имеющей
равномерное распределение на отрезке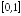 (значения
(значения можно получить путем обращения к датчику
случайных чисел, входящему в стандартное
математическое обеспечение любого
персонального компьютера).
можно получить путем обращения к датчику
случайных чисел, входящему в стандартное
математическое обеспечение любого
персонального компьютера).