
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
28. Многомерное нормальное распределение и его свойства.
Нормальное распределение в одномерном случае задается плотностью вероятностей вида:
 ,
,
причем
параметры
 (предполагается, что
(предполагается, что ,
иначе распределение является вырожденным).
,
иначе распределение является вырожденным).
Определение.
Говорят, что непрерывный случайный
вектор
 имеетмногомерное
нормальное (гауссовское) распределение,
если его плотность вероятностей имеет
вид:
имеетмногомерное
нормальное (гауссовское) распределение,
если его плотность вероятностей имеет
вид:
 ,
(3.19)
,
(3.19)
где
 - математическое ожидание случайного
вектора
- математическое ожидание случайного
вектора ;
; - корреляционная матрица случайного
вектора
- корреляционная матрица случайного
вектора ;
; - определитель корреляционной матрицы
- определитель корреляционной матрицы (предполагается, что
(предполагается, что );
); – алгебраическое дополнение к элементу
– алгебраическое дополнение к элементу матрицы
матрицы (так, что
(так, что - элемент матрицы, обратной к
- элемент матрицы, обратной к ).
).
Несколько более компактно выглядит запись для многомерной нормальной плотности вероятностей в векторной форме:
 ,
,
где верхний индекс «Т» означает знак транспонирования.
Далее
будет использоваться для нормального
случайного вектора краткая запись:
 .
.
Из
выражения (3.19) для плотности вероятностей
видно, что нормальный закон распределения
полностью
определяется моментами первых двух
порядков: математическими ожиданиями
 ,
дисперсиями
,
дисперсиями и корреляционными моментами
и корреляционными моментами .
.
Если
случайный вектор
 и его координаты являютсяпопарно
некоррелированными
случайными величинами, то есть
и его координаты являютсяпопарно
некоррелированными
случайными величинами, то есть
 ,
то корреляционная матрица
,
то корреляционная матрица и обратная к ней
и обратная к ней являются диагональными
являются диагональными

 ,
,
 .
.
Поэтому из (3.19) следует, что

 ,
,
где
 - плотности вероятностей одномерного
нормального распределения с параметрами
- плотности вероятностей одномерного
нормального распределения с параметрами .
Но это означает независимость случайных
величин
.
Но это означает независимость случайных
величин .
.
Таким образом, для нормально распределенных случайных величин понятия независимости и некоррелированности совпадают (эквивалентны).
Другие замечательные свойства многомерного нормального распределения.
Если
 ,
то:
,
то:
Все координаты
 имеют одномерные нормальные распределения:
имеют одномерные нормальные распределения: (уметь доказывать при
(уметь доказывать при ).
).Все условные законы распределения являются нормальными (уметь доказывать при
 ).
).Если координаты
 являются независимыми случайными
величинами, то любая их линейная
комбинация
являются независимыми случайными
величинами, то любая их линейная
комбинация также является нормальной случайной
величиной:
также является нормальной случайной
величиной: (уметь доказывать при
(уметь доказывать при с помощью интеграла свертки).
с помощью интеграла свертки).
Рассмотрим
подробнее случай
 .
Пусть
.
Пусть - непрерывный случайный вектор, у которого
- непрерывный случайный вектор, у которого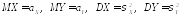 .
В этом случае корреляционная матрица
случайного вектора
.
В этом случае корреляционная матрица
случайного вектора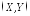 имеет вид:
имеет вид: ,
а определитель корреляционной матрицы
,
а определитель корреляционной матрицы .
.
Поэтому
плотность вероятностей двумерного
нормального случайного вектора
 имеет вид:
имеет вид:

 .
.
Для
двумерного нормального случайного
вектора
 используется краткая запись:
используется краткая запись: (зависит от пяти параметров).
(зависит от пяти параметров).
График
двумерной плотности вероятностей
 имеет вид:
имеет вид:

Линиями уровня двумерной плотности вероятностей являются эллипсы:

Найдем
одномерные плотности вероятностей
 и
и координат случайного вектора
координат случайного вектора .
.


 ,
,
то
есть
 .
.
Аналогично,
 ,
то есть
,
то есть .
.
Таким
образом, у двумерного нормального
случайного вектора
 одномерные законы распределениявсегда
являются нормальными.
одномерные законы распределениявсегда
являются нормальными.
Найдем
условные законы распределения, если
случайный вектор
 .
.


Из
полученного вида условной плотности
вероятностей
 следует, что она является плотностью
вероятностей нормального закона
распределения с параметрами
следует, что она является плотностью
вероятностей нормального закона
распределения с параметрами
 и
и
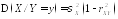 .
.
Полностью аналогично получаем, что условная плотность вероятностей

является плотностью вероятностей нормального закона распределения с параметрами
 и
и
 .
.
Таким
образом, если
 - двумерный нормальный случайный вектор,
то условные математические ожидания
- двумерный нормальный случайный вектор,
то условные математические ожидания и
и являются линейными функциями условия
(или, другими словами, в нормальном
случае уравнения регрессии являются
линейными), а условные дисперсии
являются линейными функциями условия
(или, другими словами, в нормальном
случае уравнения регрессии являются
линейными), а условные дисперсии и
и являются постоянными величинами.
являются постоянными величинами.
