
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
Свойства операций над событиями

2. Классическое определение вероятности. Урновая схема. Пример.
Говорят, что случайный эксперимент удовлетворяет классическому определению вероятности(или классической вероятностной схеме), если:
пространство элементарных событий состоит из конечногочисла исходов
 ;
;
все элементарные исходы эксперимента являются равновозможными (т. е. ни один из исходов не имеет предпочтения перед другими).
Согласно
классическому
определению вероятности вероятность
любого события
 ,
,


 равна отношению числа
равна отношению числа исходов,благоприятствующих
событию
исходов,благоприятствующих
событию
 ,
к общему числу исходов
,
к общему числу исходов :
:

Свойства вероятности, непосредственно вытекающие из классического определения вероятности:
1°.
 для любого событияА
(доказательство
очевидно).
для любого событияА
(доказательство
очевидно).
2°.
 (доказательство
очевидно).
(доказательство
очевидно).
3°.
Если события
 и
и несовместны
несовместны
 ,
то
,
то
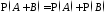 .
.
▲ Пусть событию А благоприятствует исходов, а событиюВ-
исходов, а событиюВ- исходов. Поскольку событияАиВявляются несовместными (т.е. не имеют
общих исходов), то сумме
исходов. Поскольку событияАиВявляются несовместными (т.е. не имеют
общих исходов), то сумме благоприятствует
благоприятствует исходов. Поэтому
исходов. Поэтому
 .■
.■
Исходя из свойств 1 3 (и только!!!) вытекают также следующие свойства вероятности:
4°.
 .
.
▲ Поскольку
события
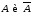 образуют полную группу событий (
образуют полную группу событий ( ),
то из свойств 2° и 3°
),
то из свойств 2° и 3° .■
.■
5°.
 .
.
▲ Следует
из свойств 2° и 4°, поскольку события
 .■
.■
6°.
 .
.
▲ Представим
событие В
в виде:
 .
Поскольку события
.
Поскольку события являются несовместными, то из свойств
1° и 3° имеем:
являются несовместными, то из свойств
1° и 3° имеем: .■
.■
7°.
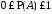 .
.
▲ Следует
из свойств 2°, 5° и 6°, так как
 (в частности, свойство 7° означает, что
измерять вероятность в процентах
некорректно).■
(в частности, свойство 7° означает, что
измерять вероятность в процентах
некорректно).■
Пример 2 (Урновая схема).
В урне находится Nшаров, из которыхMбелые. Из урны наугад извлекаетсяnшаров. Какова вероятность того, что среди выбранных шаров окажется ровноmбелых.
Решение. Исходами в данном эксперименте
являются любые подмножества, содержащие
nшаров, и они являются
равновозможными (за счет слова «наугад»).
Число всех исходов равно числу сочетаний
изnпоN: .
Каждый набор шаров, входящий в интересующее
нас событие, состоит изmбелых шаров, которые можно выбрать изMбелых
.
Каждый набор шаров, входящий в интересующее
нас событие, состоит изmбелых шаров, которые можно выбрать изMбелых способами. Независимо от выбора белых
шаров, небелые шары можно выбрать
способами. Независимо от выбора белых
шаров, небелые шары можно выбрать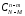 способами. Поэтому общее число
благоприятных исходов равно
способами. Поэтому общее число
благоприятных исходов равно .
Из этого следует, что
.
Из этого следует, что .
.
При решении задач с использованием классического определения вероятности, широко используются понятия комбинаторики. Напомним некоторые из них.
Размещением из N
элементов некоторого множества по M
элементов называется любой упорядоченный
набор из M элементов
данного множества. Число всех размещений
равно
 .
.
Если в упорядоченном наборе элементы
могут повторяться, то этот набор
называется размещением с
повторениями. Число размещений
с повторениями: равно .
.
Перестановкой из N
элементов некоторого множества называется
размещение из N
элементов по N.
Число всех перестановок равно
 .
.
Сочетанием из N
элементов некоторого множества по M
элементов называется любое подмножество
мощности M. Число
всех сочетаний равно
 .
.
3. Геометрическое определение вероятности. Пример.
Геометрическое определение вероятности является обобщением классического определения вероятности на случай, когда множество равновозможных исходов бесконечно.
Говорят, что случайный эксперимент удовлетворяет геометрическому определению вероятности, если:
исходы эксперимента можно изобразить точками некоторой области
 ,
имеющей конечную меру
,
имеющей конечную меру ;
;можно считать, что попадание точки в любые области
 ,
имеющие одинаковую конечную меру
,
имеющие одинаковую конечную меру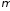 ,равновозможно
и не зависит от формы и расположения
,равновозможно
и не зависит от формы и расположения
 внутри
внутри .
При этом говорят, чтоточка
равномерно распределена
в области
.
При этом говорят, чтоточка
равномерно распределена
в области
 или бросается в область
или бросается в область наудачу.
наудачу.
Согласно
геометрическому
определению вероятности
вероятность попадания точки в любую
область
 (событие
(событие )
пропорциональна ее мере
)
пропорциональна ее мере :
:
 .
.
В частности:
при
 под мерой
под мерой понимается длина
понимается длина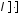 подмножества на числовой прямой
подмножества на числовой прямой и
и
 ;
;
при
 под мерой
под мерой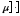 понимается площадь
понимается площадь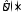 подмножества на плоскости
подмножества на плоскости и
и

A
 ;
;
при
 под мерой
под мерой понимается объем
понимается объем подмножества в пространстве
подмножества в пространстве и
и
 .
.
V
VA
Замечание.
В рассмотренной схеме событиями считаются
не любые подмножества
 ,
а только имеющие конечную меру
,
а только имеющие конечную меру
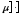 .
Данное ограничение необходимо, поскольку
в
.
Данное ограничение необходимо, поскольку
в
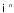 существуют неизмеримые (не имеющие
меры) множества (см. замечание из раздела
1.2, а также раздел 1.7).
существуют неизмеримые (не имеющие
меры) множества (см. замечание из раздела
1.2, а также раздел 1.7).
Из геометрического определения вероятности вытекают следующие свойства вероятности.

Следовательно, справедливы и свойства вероятности 4° – 7°, доказательство которых в классическом определении вероятности основывалось только на свойствах 1° – 3°.
Пример.
На обслуживающее устройство в промежутке
времени
 равновозможно поступление двух заявок.
Время обслуживания одной заявки равно. Если очередная
заявка поступает в момент занятости
устройства обслуживанием предыдущей,
то она теряется. Найти вероятность
потери заявки.
равновозможно поступление двух заявок.
Время обслуживания одной заявки равно. Если очередная
заявка поступает в момент занятости
устройства обслуживанием предыдущей,
то она теряется. Найти вероятность
потери заявки.
|
Решение. Обозначим t1,
t2 моменты поступления заявок.Тогда Интересующее нас событие Аимеет вид:
Поэтому (см. рисунок)
|
t2
T
t1 T
|


 .
. .
.



