- •Теоретическая механика
- •Основные понятия и аксиомы статики
- •1.1.1 Основные понятия
- •1.1.2 Аксиомы статики
- •1.3 Сложение сил на плоскости
- •1.3.1 Векторный (геометрический) способ сложения сил.
- •1.4.2 Теорема о трех непараллельных силах.
- •1.5 Вопросы для самоконтроля
- •2.1 Момент силы относительно центра (точки). Теорема Вариньона
- •2.1.1 Момент силы относительно центра.
- •2.1.2 Теорема Вариньона.
- •2.2 Теория пар сил, свойства пар сил
- •2.2.1 Основные понятия.
- •2.2.2 Свойства пар сил.
- •Приведение сил к заданному центру
- •2.3.1 Лемма Пуансо.
- •2.3.2 Теорема Пуансо.
- •2 .3.3 Частные случаи.
- •2.5 Вопросы для самоконтроля
- •3.1 Параллельные силы
- •Основная форма условий равновесия.
- •Вторая форма условий равновесия:
- •3.2 Распределенные нагрузки
- •3.3 Равновесие системы тел
- •3.4 Вопросы для самоконтроля
- •4.1 Момент силы относительно оси
- •4.2 Пространственная система сил
- •Уравнения равновесия произвольной пространственной системы сил в аналитической форме имеют вид:
- •Аналитические условия равновесия различных систем сил
- •4.4 Вопросы для самоконтроля
- •5.1 Трение
- •5.1.1 Трение скольжения
- •5.1.2 Трение качения
- •5.1.3 Трение верчения
- •5 .2 Центр тяжести твердого тела
- •5 .3 Статическая устойчивость
- •5.3.1 Устойчивость при опрокидывании
- •5.3.2 Устойчивость трактора на склоне
- •5.4 Вопросы для самоконтроля
- •Лекция №6
- •6.1 Основные понятия кинематики
- •6.2 Векторный способ задания движения точки
- •6.3 Координатный способ задания движения точки
- •Естественный способ задания движения точки
- •7.1 Поступательное движение твердого тела
- •7 .2 Вращательное движение твердого тела
- •7.3 Передаточные механизмы
- •7.4 Вопросы для самоконтроля
- •8.1 Плоское движение твердого тела
- •8.1.1 Свойства плоского движения:
- •8.1.2 Теорема сложения скоростей плоской фигуры:
- •8.1.4 Теорема о сложении ускорений плоской фигуры
- •8.2 Сложное движение точки (тела)
- •8.2.3 Сложение вращательных движений твердого тела
- •8.3 Вопросы для самоконтроля
- •Лекция №9
- •9.1 Законы динамики (Ньютона)
- •9.2 Системы единиц в механике
- •9.3 Дифференциальные уравнения движения материальной точки
- •9.3.1 Уравнения движения точки в декартовых координатах
- •9.3.2 Уравнение движения точки в естественных координатах
- •9.4 Вопросы для самоконтроля
- •10.1 Гармонические колебания точки под действием восстанавливающей силы
- •Свойства свободных гармонических колебаний:
- •А мплитуда а и начальная фаза α зависят от начальных условий;
- •Затухающие колебания точки при линейном законе сопротивления среды
- •10.3 Вопросы для самоконтроля
- •11.1 Вынужденные колебания точки в отсутствие сопротивления среды
- •11.2 Вынужденные колебания точки при вязком сопротивлении среды
- •11.3 Вопросы для самоконтроля
- •12.1 Относительное движение точки
- •12.1.1 Принципы относительности
- •Обозначим: - переносная сила инерции;
- •12.1.3 Сила тяготения, сила тяжести, вес.
- •12.2 Механическая система
- •12.2.2 Масса системы. Центр масс
- •12.2.6 Главные оси инерции
- •12.3 Вопросы для самоконтроля
- •13.1 Работа силы
- •13.1.6 Графический способ вычисления работы силы
- •1 3.1.7 Теоремы о работе силы:
- •13.1.8 Работа сил приложенных к вращающемуся телу
- •13.2 Мощность. Коэффициент полезного действия
- •13.3 Кинетическая энергия
- •Неизменяемая система
- •Система с идеальными связями
- •13.4 Вопросы для самоконтроля
- •14.1 Количество движения точки и системы. Импульс силы
- •14.2 Момент количества движения (кинетический момент)
- •14.3 Уравнение вращательного движения твердого тела
- •14.4 Уравнения плоского движения твердого тела
- •14.5 Вопросы для самоконтроля
- •15.1 Принцип Даламбера
- •15.2 Реакции, действующие на ось вращающегося тела
- •15.3 Вопросы для самоконтроля
- •16.1 Классификация связей
- •16.2 Возможные перемещения системы
- •16.3 Обобщенные координаты. Число степеней свободы системы
- •16.4 Принцип возможных перемещений
- •16.4.2 Примеры простейших механизмов:
- •16.5 Общее уравнение динамики
- •16.6 Вопросы для самоконтроля
- •17.1 Обобщенные скорости
- •17.2 Обобщенные силы
- •17.3 Уравнения Лагранжа (второго рода)
- •17.4 Вопросы для самоконтроля
- •18.1 Теория удара. Основные понятия и теоремы
- •18.1.1 Основные понятия.
- •18.2 Удар точки о неподвижную поверхность
- •1 8.2.1 Прямой удар.
- •18.2.2 Косой удар
- •18.2.3 Экспериментальное определение коэффициента восстановления.
- •18.2.4 Теоремы Карно.
- •18.3 Центральный удар двух тел
- •18.3.1 Прямой центральный удар.
- •18.4 Удар по телу, имеющему ось вращения. Центр удара
- •18.5 Вопросы для самоконтроля
7.3 Передаточные механизмы
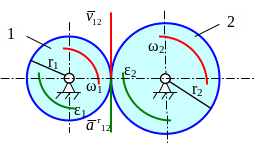
Передаточные механизмы служат для передачи и преобразования движения от одного звена механизма к другому. Для передачи вращательного движения служат различные зубчатые, фрикционные, ременные, цепные передачи. Простейшие из них - с параллельными неподвижными осями вращения.
К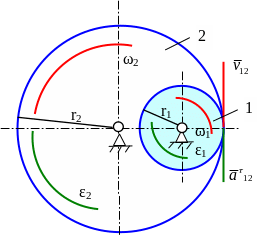 олеса
с внутренним и внешним зацеплением:
олеса
с внутренним и внешним зацеплением:
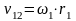 ;
;
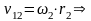
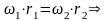
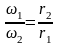 .
.


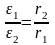 .
.
Для колес с внешним зацеплением направления ω1 и ω2, ε1 и ε2 противоположны. Для колес с внутренним зацеплением – одинаковы.
Р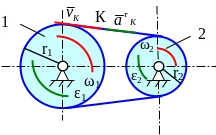 еменные
(цепные) передачи:
еменные
(цепные) передачи:
Каждая точка ремня (цепи) в данный момент имеет скорость равную скорости точки К.
 .
.
У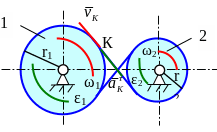 гловые
скорости колес направлены в сторону,
указанную вектором
гловые
скорости колес направлены в сторону,
указанную вектором
.
Каждая точка ремня (цепи) имеет ускорение
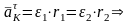
Угловые
ускорения колес направлены в сторону
указанную вектором
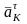 .
.
7.4 Вопросы для самоконтроля
Перечислите простейшие виды движения твердого тела.
Какое движение твердого тела называется поступательным? Перечислите свойства поступательного движения.
Какое движение называется мгновенно поступательным?
Какое движение называется вращательным? Что такое угол поворота тела?
Что называют угловой скоростью тела? Угловым ускорением?
Как соотносятся угловая скорость и угловое ускорение тела при ускоренном движении? При замедленном движении? При равнопеременном движении?
Запишите закон равноускоренного вращения тела.
Как определяются скорость, нормальное, касательное, полное ускорения точки тела вращения по модулю и направлению?
Для чего предназначены передаточные механизмы. Перечислите простейшие из них с неподвижными осями вращения.
З
 апишите
формулы, устанавливающие соотношения
между угловыми скоростями и их радиусами,
между угловыми ускорениями и радиусами.
апишите
формулы, устанавливающие соотношения
между угловыми скоростями и их радиусами,
между угловыми ускорениями и радиусами.
ЛЕКЦИЯ №8
8.1 Плоское движение твердого тела
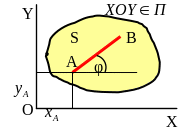
Движение твердого тела называется плоским (плоскопараллельным), если каждая точка тела движется в одной и той же плоскости.
8.1.1 Свойства плоского движения:
т
 очки
тела движутся в плоскостях параллельных
между собой и некоторой фиксированной
плоскости П0;
очки
тела движутся в плоскостях параллельных
между собой и некоторой фиксированной
плоскости П0;траектории точек – плоские кривые;
для изучения плоского движения тела достаточно изучить движение плоской фигуры S в сечении плоскостью П÷÷ П0;
положение плоской фигуры S однозначно определяется положением в этом сечении отрезка АВ; положение отрезка АВ однозначно определяется координатами произвольно выбранной точки А (полюса) и углом φ:
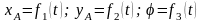 - уравнения
плоского движения твердого тела;
- уравнения
плоского движения твердого тела;
д
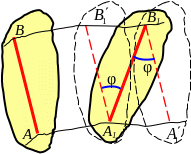 вижение
плоской фигуры S
в ее плоскости П
может рассматриваться как сумма
поступательного движения
всех точек фигуры, движущихся как полюс
– точка А
и
вращения
фигуры S
вокруг этого полюса;
вижение
плоской фигуры S
в ее плоскости П
может рассматриваться как сумма
поступательного движения
всех точек фигуры, движущихся как полюс
– точка А
и
вращения
фигуры S
вокруг этого полюса;поступательное движение полюса и угол поворота φ не зависят от выбора полюса.
8.1.2 Теорема сложения скоростей плоской фигуры:
Т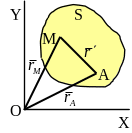 еорема:
Скорость любой точки (М)
плоской фигуры геометрически складывается
из скорости какой-либо другой точки
(А),
принятой за полюс и скорости, которую
данная точка (М)
получит при вращении фигуры вокруг
полюса.
еорема:
Скорость любой точки (М)
плоской фигуры геометрически складывается
из скорости какой-либо другой точки
(А),
принятой за полюс и скорости, которую
данная точка (М)
получит при вращении фигуры вокруг
полюса.
Доказательство
Так
как
 ,
то
,
то
 .
.
В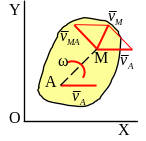 ектор
ектор
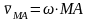 и
направлен перпендикулярно АМ
в сторону указанную угловой скоростью
ω.
Модуль
и направление вектора
и
направлен перпендикулярно АМ
в сторону указанную угловой скоростью
ω.
Модуль
и направление вектора
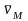 определяют
по правилу параллелограмма. Векторное
уравнение
определяют
по правилу параллелограмма. Векторное
уравнение
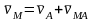 может быть решено аналитически (для
этого его проецируют на оси координат)
и графически (строят план скоростей,
см. ниже).
может быть решено аналитически (для
этого его проецируют на оси координат)
и графически (строят план скоростей,
см. ниже).
8.1.3 Планом скоростей называется векторная диаграмма, построенная на основе теоремы сложения скоростей. Покажем порядок построения плана скоростей для кривошипно-ползунного механизма – широко распространенного в сельхозмашиностроении и других отраслях.
К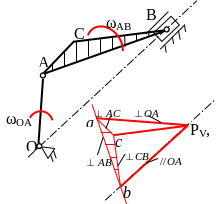 ривошипно-ползунный
механизм состоит из трех подвижных
звеньев: кривошипа ОА;
шатуна АВС;
ползуна (поршня) В
и неподвижной стойки (заштриховано).
Если заданы: положение механизма, угловая
скорость кривошипа ωОА,
длины звеньев
ривошипно-ползунный
механизм состоит из трех подвижных
звеньев: кривошипа ОА;
шатуна АВС;
ползуна (поршня) В
и неподвижной стойки (заштриховано).
Если заданы: положение механизма, угловая
скорость кривошипа ωОА,
длины звеньев
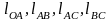 ,
то можно рассчитать модуль скорости
точки А
по формуле
,
то можно рассчитать модуль скорости
точки А
по формуле
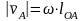 ;
вектор
;
вектор
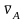 направлен перпендикулярно кривошипу
ОА в сторону, указанную
направлен перпендикулярно кривошипу
ОА в сторону, указанную
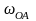 .
.
Из произвольной точки РV (полюс плана скоростей) отложим в масштабе вектор , его конец обозначим буквой а. Шатун АВ совершает плоское движение, применим к нему теорему сложения скоростей
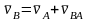 .
.
Из
конца вектора
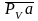 проведем перпендикуляр к АВ,
а из полюса плана PV//OB.
Точку пересечения обозначим b.
Проведем из полюса PV
стрелки к точкам a
и b.
Это в масштабе векторы скоростей
и
проведем перпендикуляр к АВ,
а из полюса плана PV//OB.
Точку пересечения обозначим b.
Проведем из полюса PV
стрелки к точкам a
и b.
Это в масштабе векторы скоростей
и
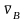 .
Вектор
.
Вектор
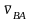 изображен на плане скоростей отрезком
ab
и направлен от a
к b.
изображен на плане скоростей отрезком
ab
и направлен от a
к b.
Чтобы определить скорость точки С шатуна составим по теореме сложения скоростей два векторных уравнения, приняв за полюсы точки А и В:

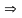
Чтобы
совместно графически решить эти
уравнения, проведем из точки
a
плана скоростей перпендикуляр к АС,
а из точки b
перпендикуляр к ВС.
Точку их пересечения обозначим с.
Стрелка из полюса плана скоростей PV
к точке c
– в масштабе вектор
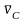 .
План построен.
.
План построен.
Свойства плана скоростей:
масштаб плана скоростей определяется по заданному вектору скорости (
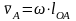 или
)
с помощью масштабного коэффициента
или
)
с помощью масштабного коэффициента
 ,
который рассчитывают разделив модуль
заданной скорости на выбранную длину,
например,
,
который рассчитывают разделив модуль
заданной скорости на выбранную длину,
например,
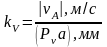 ;
;полюс плана скоростей точка PV, в этой точке находятся точки, скорость которых равна нулю (например, неподвижная точка стойки О;
скорость любой точки механизма относительно стойки (например, ) изображается отрезком, направленным от полюса плана PV к соответствующей точке (отрезок Pvc);
скорость вращения одной точки какого-либо звена вокруг другой (например, точки С вокруг точки А -
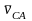 )
изображается одноименным отрезком
(ac),
направлен вектор к той точке, которую
вращают (к точке с);
)
изображается одноименным отрезком
(ac),
направлен вектор к той точке, которую
вращают (к точке с);модуль угловой скорости звена равен частному от деления скорости вращения одной точки этого звена вокруг другой на натуральную длину расстояния между точками на звене механизма (например,
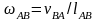 );
);модуль любой скорости механизма можно определить, умножив длину соответствующего отрезка на плане скоростей на масштабный коэффициент (например,
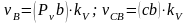 );
);если на плане найдены скорости двух точек звена, то скорость любой другой точки этого звена можно найти по правилу подобия: если на звене механизма точки образуют геометрическую фигуру, то одноименные точки на плане скоростей образуют подобную сходственно расположенную (повернутую в плоскости чертежа) фигуру (например,
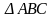 ~
~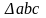 ).
).
8.1.4
Мгновенный центр скоростей
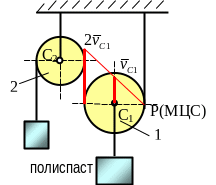
Наиболее просто находить скорости точек плоской фигуры при помощи мгновенного центра скоростей (МЦС).
Теорема: В каждый момент времени при плоском движении фигуры, если ее угловая скорость не равна нулю (ω≠0), то в ее плоскости есть единственная точка этой фигуры (или жестко с ней связанная), скорость которой равна нулю. Эту точку называют мгновенным центром скоростей.
С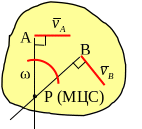 ледствие:
ледствие:
чтобы определить положение МЦС надо знать направление скоростей двух точек фигуры – МЦС лежит на пересечении перпендикуляров к векторам скоростей, проведенным из этих точек;
для определения с помощью МЦС скорости любой точки плоской фигуры надо знать модуль и направление скорости одной точки и направление другой;
угловая скорость плоской фигуры в любой момент времени равна отношению скорости любой точки к ее расстоянию до МЦС (например,
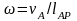 );
направление ω
указывает скорость точки;
);
направление ω
указывает скорость точки;если ω=0, то МЦС не существует.
В некоторых случаях МЦС, то есть неподвижная в данный момент точка тела Р (плоской фигуры), заранее известна, что позволяет находить скорости других точек тела.