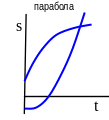- •Теоретическая механика
- •Основные понятия и аксиомы статики
- •1.1.1 Основные понятия
- •1.1.2 Аксиомы статики
- •1.3 Сложение сил на плоскости
- •1.3.1 Векторный (геометрический) способ сложения сил.
- •1.4.2 Теорема о трех непараллельных силах.
- •1.5 Вопросы для самоконтроля
- •2.1 Момент силы относительно центра (точки). Теорема Вариньона
- •2.1.1 Момент силы относительно центра.
- •2.1.2 Теорема Вариньона.
- •2.2 Теория пар сил, свойства пар сил
- •2.2.1 Основные понятия.
- •2.2.2 Свойства пар сил.
- •Приведение сил к заданному центру
- •2.3.1 Лемма Пуансо.
- •2.3.2 Теорема Пуансо.
- •2 .3.3 Частные случаи.
- •2.5 Вопросы для самоконтроля
- •3.1 Параллельные силы
- •Основная форма условий равновесия.
- •Вторая форма условий равновесия:
- •3.2 Распределенные нагрузки
- •3.3 Равновесие системы тел
- •3.4 Вопросы для самоконтроля
- •4.1 Момент силы относительно оси
- •4.2 Пространственная система сил
- •Уравнения равновесия произвольной пространственной системы сил в аналитической форме имеют вид:
- •Аналитические условия равновесия различных систем сил
- •4.4 Вопросы для самоконтроля
- •5.1 Трение
- •5.1.1 Трение скольжения
- •5.1.2 Трение качения
- •5.1.3 Трение верчения
- •5 .2 Центр тяжести твердого тела
- •5 .3 Статическая устойчивость
- •5.3.1 Устойчивость при опрокидывании
- •5.3.2 Устойчивость трактора на склоне
- •5.4 Вопросы для самоконтроля
- •Лекция №6
- •6.1 Основные понятия кинематики
- •6.2 Векторный способ задания движения точки
- •6.3 Координатный способ задания движения точки
- •Естественный способ задания движения точки
- •7.1 Поступательное движение твердого тела
- •7 .2 Вращательное движение твердого тела
- •7.3 Передаточные механизмы
- •7.4 Вопросы для самоконтроля
- •8.1 Плоское движение твердого тела
- •8.1.1 Свойства плоского движения:
- •8.1.2 Теорема сложения скоростей плоской фигуры:
- •8.1.4 Теорема о сложении ускорений плоской фигуры
- •8.2 Сложное движение точки (тела)
- •8.2.3 Сложение вращательных движений твердого тела
- •8.3 Вопросы для самоконтроля
- •Лекция №9
- •9.1 Законы динамики (Ньютона)
- •9.2 Системы единиц в механике
- •9.3 Дифференциальные уравнения движения материальной точки
- •9.3.1 Уравнения движения точки в декартовых координатах
- •9.3.2 Уравнение движения точки в естественных координатах
- •9.4 Вопросы для самоконтроля
- •10.1 Гармонические колебания точки под действием восстанавливающей силы
- •Свойства свободных гармонических колебаний:
- •А мплитуда а и начальная фаза α зависят от начальных условий;
- •Затухающие колебания точки при линейном законе сопротивления среды
- •10.3 Вопросы для самоконтроля
- •11.1 Вынужденные колебания точки в отсутствие сопротивления среды
- •11.2 Вынужденные колебания точки при вязком сопротивлении среды
- •11.3 Вопросы для самоконтроля
- •12.1 Относительное движение точки
- •12.1.1 Принципы относительности
- •Обозначим: - переносная сила инерции;
- •12.1.3 Сила тяготения, сила тяжести, вес.
- •12.2 Механическая система
- •12.2.2 Масса системы. Центр масс
- •12.2.6 Главные оси инерции
- •12.3 Вопросы для самоконтроля
- •13.1 Работа силы
- •13.1.6 Графический способ вычисления работы силы
- •1 3.1.7 Теоремы о работе силы:
- •13.1.8 Работа сил приложенных к вращающемуся телу
- •13.2 Мощность. Коэффициент полезного действия
- •13.3 Кинетическая энергия
- •Неизменяемая система
- •Система с идеальными связями
- •13.4 Вопросы для самоконтроля
- •14.1 Количество движения точки и системы. Импульс силы
- •14.2 Момент количества движения (кинетический момент)
- •14.3 Уравнение вращательного движения твердого тела
- •14.4 Уравнения плоского движения твердого тела
- •14.5 Вопросы для самоконтроля
- •15.1 Принцип Даламбера
- •15.2 Реакции, действующие на ось вращающегося тела
- •15.3 Вопросы для самоконтроля
- •16.1 Классификация связей
- •16.2 Возможные перемещения системы
- •16.3 Обобщенные координаты. Число степеней свободы системы
- •16.4 Принцип возможных перемещений
- •16.4.2 Примеры простейших механизмов:
- •16.5 Общее уравнение динамики
- •16.6 Вопросы для самоконтроля
- •17.1 Обобщенные скорости
- •17.2 Обобщенные силы
- •17.3 Уравнения Лагранжа (второго рода)
- •17.4 Вопросы для самоконтроля
- •18.1 Теория удара. Основные понятия и теоремы
- •18.1.1 Основные понятия.
- •18.2 Удар точки о неподвижную поверхность
- •1 8.2.1 Прямой удар.
- •18.2.2 Косой удар
- •18.2.3 Экспериментальное определение коэффициента восстановления.
- •18.2.4 Теоремы Карно.
- •18.3 Центральный удар двух тел
- •18.3.1 Прямой центральный удар.
- •18.4 Удар по телу, имеющему ось вращения. Центр удара
- •18.5 Вопросы для самоконтроля
6.3 Координатный способ задания движения точки
При координатном способе закон движения точки (уравнения движения точки) в пространстве задается тремя координатами (декартовыми координатами) как функциями времени:
X = f1(t); Y = f2(t); Z = f3(t);
на плоскости – двумя координатами:
X = f1(t); Y = f2(t);
при прямолинейном движении – одной координатой:
X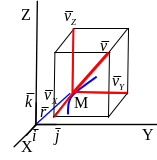 = f1(t).
= f1(t).
Для получения уравнения траектории точки из уравнений движения исключают время.
Так как , то скорость точки равна:
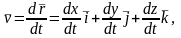 но
но

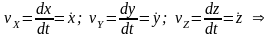
Проекции вектора скорости на оси декартовых координат равны первым производным от соответствующих координат по времени.
Модуль вектора скорости равен
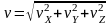 .
.
Вектор образует с осями координат углы, определяемые направляющими косинусами
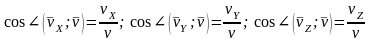 .
.
Ускорение точки равно:
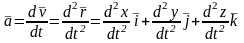 .
.
С другой стороны
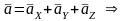
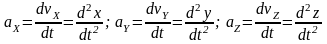
Проекции вектора ускорения на оси декартовых координат равны первым производным от проекций скорости или вторым производным от координат точки по времени.
М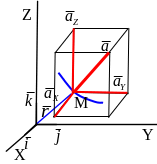 одуль
вектора ускорения равен:
одуль
вектора ускорения равен:
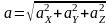 ;
;
Углы вектора ускорения с осями координат:
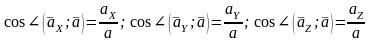 .
.
Естественный способ задания движения точки
Для применения естественного способа задания движения точки должна быть известна ее траектория. Траектория может быть задана различными способами:
уравнениями (возможно с неравенствами), например,
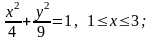
словесно, например, радиус окружности равен 3м;
в виде графика в масштабе.
Для задания закона движения точки по известной траектории необходимо:
в
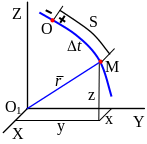 ыбрать
на траектории начало отсчета расстояний
– точку О и указать направление
положительного отсчета (знак «+»);
ыбрать
на траектории начало отсчета расстояний
– точку О и указать направление
положительного отсчета (знак «+»);выбрать начало отсчета времени t =0, обычно за начало отсчета времени принимают или начало движения или момент времени, когда движущаяся точка М проходит через точку О.
Закон движения точки М по траектории имеет вид:
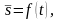
где
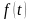 - непрерывная дважды дифференцируемая
функция, причем это выражение определяет
положение точки на траектории, но не
пройденный ею путь.
- непрерывная дважды дифференцируемая
функция, причем это выражение определяет
положение точки на траектории, но не
пройденный ею путь.
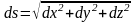 .
.
Если
при
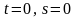 ,
то
,
то
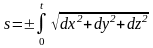 .
.
Если известен закон движения точки в декартовых координатах, то
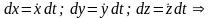
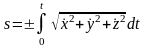 ,
,
где знак «+» или «–» определяется выбором положительного или отрицательного направления отсчета расстояний по траектории. Это выражение устанавливает связь естественного способа задания движения точки с координатным.
Скорость точки равна:
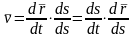 ,
,
Н о
о
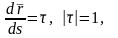 единичный
вектор
единичный
вектор
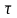 направлен
по касательной к траектории в сторону
движения точки М,
следовательно,
скорость точки М
направлена по касательной к траектории
в сторону движения и равна
направлен
по касательной к траектории в сторону
движения точки М,
следовательно,
скорость точки М
направлена по касательной к траектории
в сторону движения и равна
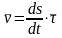 .
.
С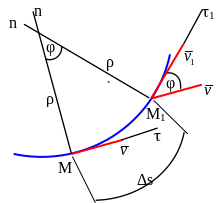 овместим
с движущейся по траектории точкой М
начало подвижной системы координат –
оси
естественного трехгранника
Мtnb.
Ось
Mt
- касательную
направим по касательной к траектории
в сторону движения точки. Ось Мn
– главную
нормаль
направим перпендикулярно Мt
в сторону вогнутости траектории так,
чтобы эти оси образовали соприкасающуюся
плоскость.
Ось Мb-
бинормаль
направим перпендикулярно соприкасающейся
плоскости в сторону, откуда поворот от
оси Мt
к оси Mn
виден против хода часовой стрелки.
Образовались еще две координатные
плоскости: Mnb
- нормальная
и Mtb
– спрямляющая.
овместим
с движущейся по траектории точкой М
начало подвижной системы координат –
оси
естественного трехгранника
Мtnb.
Ось
Mt
- касательную
направим по касательной к траектории
в сторону движения точки. Ось Мn
– главную
нормаль
направим перпендикулярно Мt
в сторону вогнутости траектории так,
чтобы эти оси образовали соприкасающуюся
плоскость.
Ось Мb-
бинормаль
направим перпендикулярно соприкасающейся
плоскости в сторону, откуда поворот от
оси Мt
к оси Mn
виден против хода часовой стрелки.
Образовались еще две координатные
плоскости: Mnb
- нормальная
и Mtb
– спрямляющая.
Пусть
точка М
переместилась в положение М1.
Векторы ее скорости в этих точках
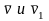 образуют
угол
смежности
φ.
образуют
угол
смежности
φ.
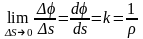 ,
,
k – кривизна кривой в точке М,
ρ – радиус кривизны кривой в точке М.
Ускорение точки М равно:
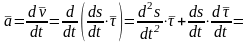

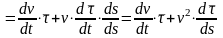 ,
,
н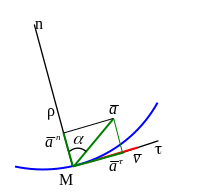 о
о
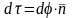 ,
следовательно
,
следовательно
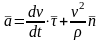 .
.
Вектор ускорения точки М разложен на две взаимно перпендикулярные составляющие лежащие в соприкасающейся плоскости:
 -
касательное
(тангенциальное) ускорение,
направленное по касательной к траектории,
характеризующее изменение
скорости по величине;
-
касательное
(тангенциальное) ускорение,
направленное по касательной к траектории,
характеризующее изменение
скорости по величине;
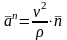 -
нормальное
(центростремительное) ускорение,
направленное перпендикулярно касательному
в сторону вогнутости траектории,
характеризующее изменение
скорости по направлению.
-
нормальное
(центростремительное) ускорение,
направленное перпендикулярно касательному
в сторону вогнутости траектории,
характеризующее изменение
скорости по направлению.
Модуль ускорения равен:
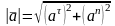
Направление ускорения по отношению к нормали определяется углом α:
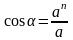 .
.
6.5 Частные случаи движения точки
6.5.1 Прямолинейное движение
Так
как траектория точки - прямая линия, то
r®
¥,
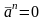 и полное ускорение
и полное ускорение
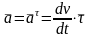 ,
направлено по прямой так же как и скорость
,
если точка
движется ускоренно
и в противоположном направлении, если
замедленно.
Ускорение меняется только по величине.
Если
,
направлено по прямой так же как и скорость
,
если точка
движется ускоренно
и в противоположном направлении, если
замедленно.
Ускорение меняется только по величине.
Если
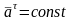 ,
то точка движется равнопеременно
или равнозамедленно
или
равноускоренно
,
то точка движется равнопеременно
или равнозамедленно
или
равноускоренно
6.5.2 Равномерное криволинейное движение
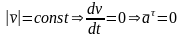
Полное
ускорение
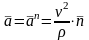 и направлено по радиусу кривизны в
сторону вогнутости. Ускорение меняется
только по направлению.
и направлено по радиусу кривизны в
сторону вогнутости. Ускорение меняется
только по направлению.
6.5.3 Равномерное прямолинейное движение
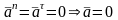 .
Точка
движется по прямой с постоянной скоростью
.
Точка
движется по прямой с постоянной скоростью
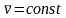 .
.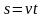 .
.
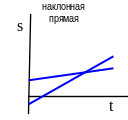
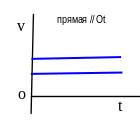
6.5.4 Графики равномерного прямолинейного или криволинейного движения имеют вид:
График движения |
График скорости |
График ускорения |
|
|
|
6.5.5 Равнопеременное криволинейное движение
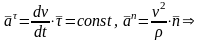
 ,
интегрируем:
,
интегрируем:
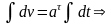
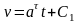
При t=0, v=v0 , C1=v0 ,
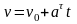 .
.
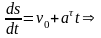
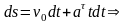
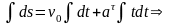
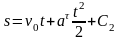 ,
,
при t =0, С2=s0 ,
Закон движения точки при ее равнопеременном криволинейном движении имеет вид:
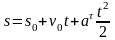 .
.
Если
направления векторов скорости
и
касательного ускорения
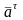 совпадают,
то точка движется равноускоренно,
если противоположны
– равнозамедленно.
совпадают,
то точка движется равноускоренно,
если противоположны
– равнозамедленно.
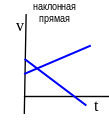
Графики равнопеременного криволинейного или прямолинейного движения точки имеют вид:
График движения |
График скорости |
График ускорения |
||
|
|
at(a) o 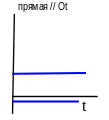
|
||
6.6 |
Вопросы для самоконтроля |
|
||
В чем состоит основная задача кинематики?
Перечислите основные способы задания движения точки.
Перечислите основные способы задания траектории движения точки.
Дайте определения понятий: скорость, ускорение, траектория движения.
Как всегда направлен по отношению к траектории вектор скорости, вектор ускорения?
Как определяются вектор скорости и ускорения по модулю и направлению при координатном способе задания движения?
Как задается закон движения точки по траектории при естественном способе задания движения?
Запишите выражение, связывающее естественный способ задания движения точки с координатным.
Изобразите оси естественного трехгранника, назовите образованные ими координатные плоскости. Является эта система координат неподвижной?
Поясните понятия: кривизна кривой, радиус кривизны.
Докажите математически как ускорение точки может быть представлено суммой нормального и касательного ускорений.
Как направлены по отношению к траектории движения точки векторы нормального и касательного ускорений? Запишите формулы для определения их модулей.
Перечислите и запишите формулы для частных случаев движения материальной точки. Покажите графики их движения.
ЛЕКЦИЯ №7