
- •Введение
- •Глава I элементы организации и процесса управления
- •1.1. Основные понятия и определения организации и управления
- •1.2. Подходы к управлению
- •1.2.1. Процессный подход
- •1.2.2. Системный подход
- •1.2.3. Ситуационный подход
- •1.3. Внутренняя среда организации
- •1.3.1. Внутренние переменные
- •1.3.2. Взаимосвязь внутренних переменных
- •Организация
- •1.4. Внешняя среда организации
- •1.4.1. Характеристики внешней среды
- •1.4.2. Среда прямого воздействия
- •1.4.3. Среда косвенного воздействия
- •1.4.4. Модель влияния внешних факторов на организацию
- •1.5.1. Классификация по виду хозяйственной деятельности
- •1.5.2. Классификация по правовому положению
- •1.5.3. Классификация по характеру собственности
- •Глава II фазы управления организацией
- •2.1. Стратегическое планирование
- •2.1.1. Сущность планирования
- •2.1.2. Цели организации
- •2.1.3. Оценка и анализ внешней среды
- •Организация Международные Социальные
- •2.1.4. Управленческое обследование внутренних сильных
- •2.1.5. Изучение стратегических альтернатив
- •2.1.6. Реализация стратегического плана
- •2.1.7. Оценка стратегического плана
- •2.2. Организация взаимодействия и полномочия
- •2.2.1. Делегирование, ответственность и полномочия
- •2.2.2. Линейные и аппаратные (штабные) полномочия
- •2.2.3. Эффективная организация распределения полномочий
- •2.3. Построение структур организаций
- •2.3.1. Выбор структуры
- •2.3.2. Департаментализация
- •Зарубежные
- •2.3.3. Адаптивные структуры
- •Блок-схема подобной структуры авиакосмического отделения фирмы «Universal Products» показана на рис. 2.18. Она напоминает решетку, отсюда и название матричная структура.
- •2.3.4. Централизованные и децентрализованные организации
- •2.4. Мотивация
- •2.4.1. Понятие мотивации
- •2.4.2. Содержательные теории мотивации
- •2.4.3. Процессуальные теории мотивации
- •2.5. Контроль
- •2.5.1. Сущность контроля
- •2.5.2. Процесс контроля
- •Глава III проектирование организационных систем
- •3.1. Системный подход
- •3.1.1. Теория организационных систем и многоуровневый
- •3.1.2. Классификация систем управления
- •3.1.3. Многоэшелонные системы – Организационные иерархии
- •Решающий элемент
- •Координация Обратная связь
- •Процесс
- •3.1.4. Основные свойства систем управления
- •3.1.5. Формализация процесса проектирования организационных систем
- •Процессы
- •3.1.6. Моделирование простого производственного объекта
- •3.1.7. Моделирование сложного производственного объекта
- •Производство
- •3.1.8. Моделирование запаздывания при освоении капитальных вложений
- •3.1.9. Моделирование многоотраслевой экономики
- •3.2. Аналитическое проектирование многоуровневых иерархических организационных систем
- •3.2.1. Построение морфологической структуры сложной системы управления
- •3.2.2. Формирование задач аналитического проектирования
- •3.2.2.1. Одноуровневая одноцелевая система
- •3.2.2.2. Одноуровневая многоцелевая система
- •3.2.2.3. Многоуровневая многоцелевая система
- •3.2.3. Выбор номинальных значений параметров целевых подсистем
- •3.2.4. Аппроксимация областей допустимых вариаций проектных
- •3.2.5. Распределение ограничений на проектные параметры
- •3.2.6. Декомпозиция главных целей на подцели подсистем нижних уровней
- •3.2.7. Выбор вариантов сложных многоуровневых систем управления
- •3.2.8. Оптимизационные методы решения задач аналитического
- •Введем условия трансверсальности
- •Введем функцию
- •3.2.9. Методы решения задач аналитического проектирования
- •Примеры аналитического проектирования организационных систем
- •4.2. Задача наискорейшего выхода предприятия на потребность
- •Критерий качества процесса
- •После времени года, развитие предприятия должно осуществляться по кривой потребности.
- •4.3. Оптимальное распределение ресурсов между предприятиями
- •Для решения оптимизационной задачи воспользуемся методом динамического программирования р. Беллмана [7, 17]. Для этого сведем ее к многошаговому управляемому процессу.
- •4.4. Оптимальная корректировка плана развития предприятия
- •Оглавление
- •Глава I. Элементы организации и процесса управления
- •Глава II. Фазы управления организацией
- •2.1.4. Управленческое обследование внутренних сильных и
- •Глава III. Проектирование организационных систем
- •3.1.3. Многоэшелонные системы - Организационные иерархии..……82
- •3.2.1. Построение морфологической структуры сложной системы управления и процедуры ее аналитического проектирования……….....107
- •3.2.2.3. Многоуровневая многоцелевая система……..…………116
- •Глава IV. Примеры аналитического проектирования
- •Список литературы………….…………………..…………………….……178
3.2.9. Методы решения задач аналитического проектирования
для одноуровневых, многоцелевых подсистем
В общем случае
задача многокритериальной оптимизации
формируется как задача одновременной
минимизации некоторой совокупности
показателей
![]() .
Следует сразу отметить, строго
математически задача с такой постановкой
смысла не имеет, так как минимум различных
критериев достигается в общем случае
при различных значениях вектора u.
Вместе с тем существует ряд способов
многокритериальной оптимизации, одни
из которых сводят задачу к однокритериальной
оптимизации путем сворачивания критериев
в один, другие – сокращают множество
исходных вариантов решений путем
неформального анализа.
.
Следует сразу отметить, строго
математически задача с такой постановкой
смысла не имеет, так как минимум различных
критериев достигается в общем случае
при различных значениях вектора u.
Вместе с тем существует ряд способов
многокритериальной оптимизации, одни
из которых сводят задачу к однокритериальной
оптимизации путем сворачивания критериев
в один, другие – сокращают множество
исходных вариантов решений путем
неформального анализа.
Простейший
способ
сведения многокритериальной задачи
оптимизации к однокритериальной состоит
в выделении одного основного критерия,
например
![]() ,
и переводе остальных критериев в разряд
ограничений
,
и переводе остальных критериев в разряд
ограничений
![]() .
.
Линейная
свертка
критериев также является широко
распространенным способом в инженерной
практике. Суть этого способа состоит в
переходе от
![]() критериев к одному
критериев к одному
![]() ,
где
,
где
![]() – весовые коэффициенты
– весовые коэффициенты
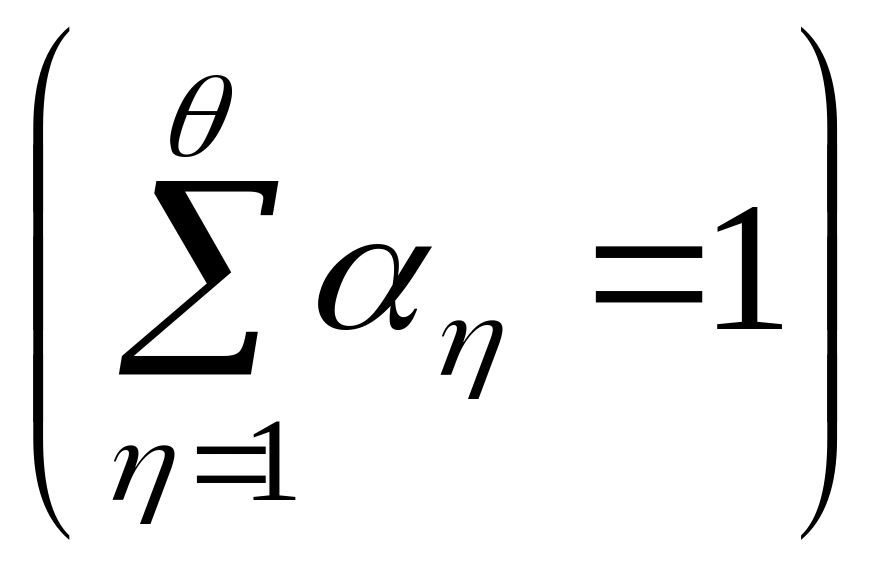 ,
характеризующие значимость соответствующего
критерия и устанавливающие определенный
компромисс между ними ранжированием
целей по их важности. Назначение
коэффициентов
является неформальным актом и
осуществляется экспертным путем.
,
характеризующие значимость соответствующего
критерия и устанавливающие определенный
компромисс между ними ранжированием
целей по их важности. Назначение
коэффициентов
является неформальным актом и
осуществляется экспертным путем.
Минимаксная
свертка сводит
многокритериальную задачу оптимизации
к отысканию гарантированного решения
в смысле близости к контрольным значениям
исходных показателей. В качестве меры
близости исходных показателей к своим
контрольным значениям
![]() используется следующая функция
используется следующая функция
![]() ,
где
– оценки сверху
,
где
– оценки сверху
![]() ,
для рассматриваемых показателей. Затем
ищется
,
для рассматриваемых показателей. Затем
ищется
![]() .
.
Использование
принципа Парето.
Сущность данного подхода состоит в
исключении из неформального анализа
таких вариантов решения, которые заведомо
являются плохими. Действительно, пусть
![]() и
и
![]() – два возможных (допустимых) варианта
решения задачи, такие, что имеют место
неравенства:
– два возможных (допустимых) варианта
решения задачи, такие, что имеют место
неравенства:
![]() ,
причем хотя бы одно из них выполняется
строго. В этом случае решение
предпочтительнее решения
.
Значит все векторы
,
удовлетворяющие этому условию, могут
быть сразу исключены из рассмотрения.
Поэтому неформальному анализу должны
быть подвергнуты лишь те векторы, для
которых не существует предпочтительных
векторов. Такие векторы называются
неулучшаемыми. Множество всех неулучшаемых
векторов принято называть множеством
Парето.
Принцип Парето заключается в том, что
в качестве оптимального решения
,
причем хотя бы одно из них выполняется
строго. В этом случае решение
предпочтительнее решения
.
Значит все векторы
,
удовлетворяющие этому условию, могут
быть сразу исключены из рассмотрения.
Поэтому неформальному анализу должны
быть подвергнуты лишь те векторы, для
которых не существует предпочтительных
векторов. Такие векторы называются
неулучшаемыми. Множество всех неулучшаемых
векторов принято называть множеством
Парето.
Принцип Парето заключается в том, что
в качестве оптимального решения
![]() должно быть выбрано только такое, которое
принадлежит множеству Парето. Необходимо
отметить, что принцип Парето не выделяет
единственное решение, а лишь сужает
множество возможных альтернатив.
должно быть выбрано только такое, которое
принадлежит множеству Парето. Необходимо
отметить, что принцип Парето не выделяет
единственное решение, а лишь сужает
множество возможных альтернатив.
Метод
основной задачи проектирования,
излагаемый в данной работе, заключается
в поиске одного из множества допустимых
решений
![]() ,
обеспечивающего нахождение всех целей
(критериев) аналитического проектирования
в заданном (допустимом) диапазоне
,
обеспечивающего нахождение всех целей
(критериев) аналитического проектирования
в заданном (допустимом) диапазоне
![]() ,
где
,
где
![]() – соответственно минимальные и
максимальные допустимые значения
критериев
– соответственно минимальные и
максимальные допустимые значения
критериев
![]() .
Необходимо отметить, что если основная
задача проектирования имеет решение,
то оно имеет не единственное решение,
а целое множество.
.
Необходимо отметить, что если основная
задача проектирования имеет решение,
то оно имеет не единственное решение,
а целое множество.
Основная задача проектирования для нелинейных подсистем и метод ее решения. Постановка задачи. Рассмотрим динамическую управляемую подсистему, математическая модель которой описывается системой обыкновенных дифференциальных уравнений [17] следующего вида:
![]() (3.129)
(3.129)
с начальными условиями
![]() .
(3.130)
.
(3.130)
Начальные условия
(3.115) и управление
![]() в соответствии с системой (3.114) задают
определенные фазовые траектории
в соответствии с системой (3.114) задают
определенные фазовые траектории
![]() (3.131)
(3.131)
Пусть на множестве допустимых управлений и траекторий определены функционалы
![]() (3.132)
(3.132)
каждый из которых представляет некоторый критерий качества функционирования динамической подсистемы, соответствующий той или иной характеристике управляемой подсистемы.
Разнообразные требования, предъявляемые к управляемым подсистемам, математически могут быть выражены ограничениями в виде неравенств
![]() .
(3.133)
.
(3.133)
Ставится следующая основная задача проектирования: среди всех допустимых управлений w найти такое, при котором решение уравнений (3.129), (3.130) обеспечивало бы выполнение требований (3.133) для функционалов (3.132).
Условие существования задачи. Если основная задача проектирования имеет решение, то, вообще говоря, оно будет не единственным. В некорректно поставленных задачах проектирования решение может вообще не существовать. Поэтому необходимо установить условия существования решения задачи аналитического проектирования и способы построения этого решения.
Введем безразмерные функционалы вместо функционалов (3.132) по формулам [18]
![]() (3.134)
(3.134)
Из выражения (3.119) следует, что если:
![]() ,
(3.135)
,
(3.135)
то
![]() (3.136)
(3.136)
Обратное утверждение также имеет место.
Введем обозначения
![]()
тогда неравенства (3.136) запишутся в виде
![]() .
(3.137)
.
(3.137)
Анализируя выражения (3.135), видим, что условие (3.137) можно заменить односторонними неравенствами
![]() ,
(3.138)
,
(3.138)
![]() ,
(3.139)
,
(3.139)
так как при выполнении (3.138) выполняется (3.139), и наоборот. В силу этого в дальнейшем будем рассматривать условие (3.138) вместо (3.159).
Теперь рассмотрим теорему, дающую условие существования решения задачи проектирования [18].
Теорема 3.6. Для того чтобы существовало решение задачи аналитического проектирования, необходимо и достаточно выполнения неравенства
![]() (3.140)
(3.140)
Алгоритм численного решения задачи. Среди методов решения минимаксных задач выделяются как наиболее эффективные так называемые прямые или пошаговые итерационные методы. Рассмотрим решение минимаксной задачи методом скорейшего спуска.
Пусть функционалы заданы в следующей форме
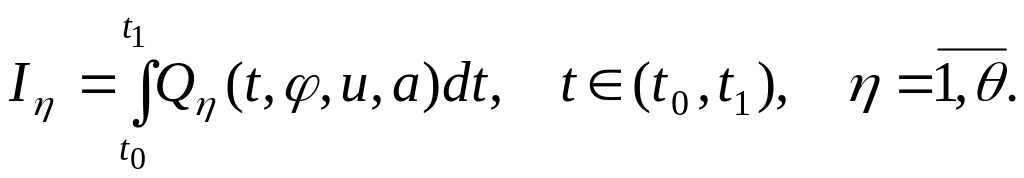 (3.141)
(3.141)
Тогда безразмерные функционалы будут иметь вид:
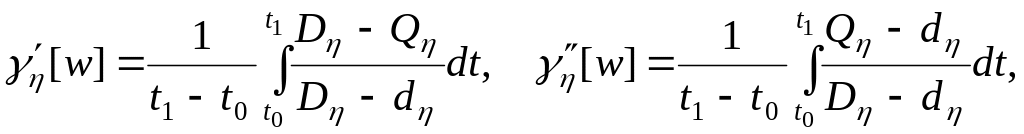 (3.142)
(3.142)
или с учетом обозначений:
![]() (3.143)
(3.143)
примут такой вид
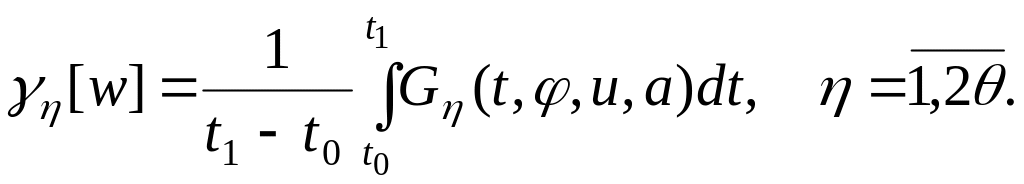 (3.144)
(3.144)
Вариации функционалов (3.144) с учетом связей (3.139) находятся обычным способом [18].
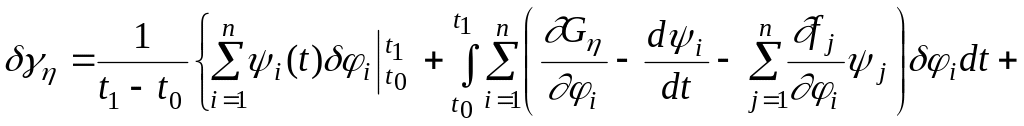
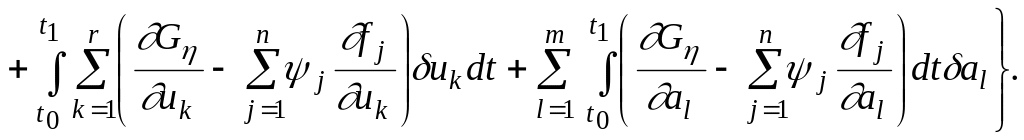
Здесь
![]() – неопределенные множители Лагранжа,
которые определяются из сопряженной
системы уравнений
– неопределенные множители Лагранжа,
которые определяются из сопряженной
системы уравнений
![]() (3.145)
(3.145)
где
![]() (3.146)
(3.146)
Учитывая выражения
(3.145), (3.146) и тот факт, что начальные
состояния (3.130) подсистемы фиксированы
![]() ,
получим следующие выражения для
,
получим следующие выражения для
![]() :
:
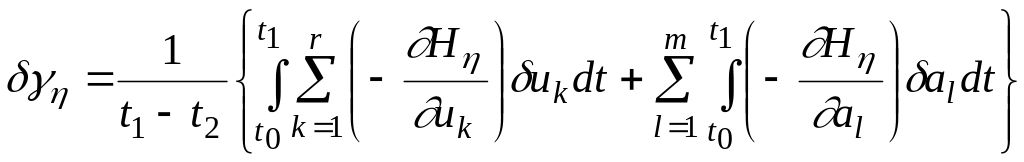 .
(3.147)
.
(3.147)
В соответствии с
методом скорейшего спуска поправки к
управлениям, уменьшающие
![]() ,
определяются соотношениями
,
определяются соотношениями
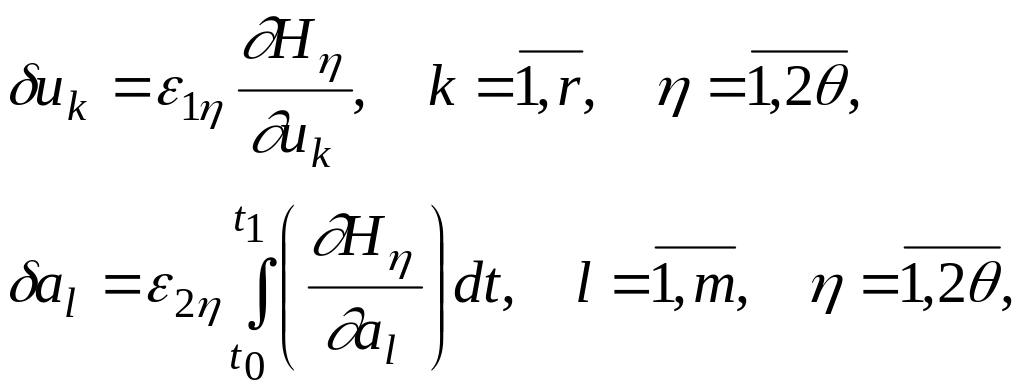 (3.148)
(3.148)
где
![]() – достаточно малые положительные
величины, определяющие шаг итерации.
– достаточно малые положительные
величины, определяющие шаг итерации.
С учетом (3.148) выражение (3.147) примет вид
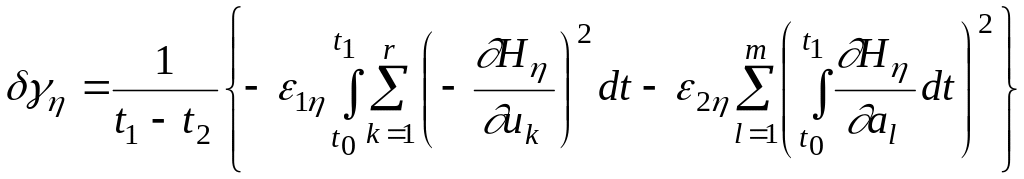 .
(3.149)
.
(3.149)
Используя полученные соотношения, можно предложить следующий алгоритм решения минимаксной задачи.
1. Задаемся нулевым приближением управляющих воздействий
![]()
2. Интегрируя уравнения (3.107) с начальными условиями (3.130), находим
![]()
3. Вычисляем значения
функционалов
![]() и находим
и находим
![]() .
.
4. Решаем в направлении
от
![]() к
к
![]() систему дифференциальных уравнений
(3.125) при
систему дифференциальных уравнений
(3.125) при
![]() и конечном условии
и конечном условии
![]() и
находим первое приближение для
и
находим первое приближение для
![]() .
.
5. Вычисляем производные
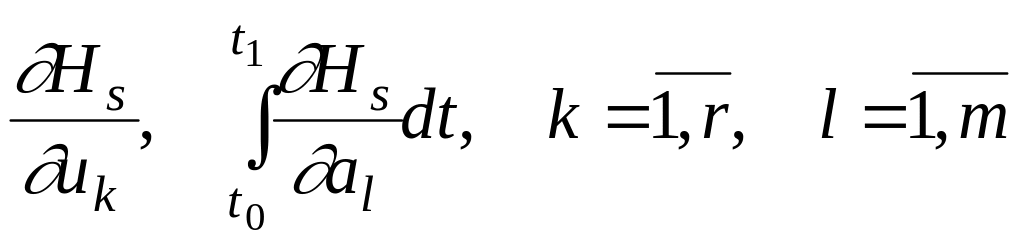
при
![]() и, задавшись достаточно малыми
положительными величинами
и, задавшись достаточно малыми
положительными величинами
![]() ,
находим поправки
,
находим поправки
![]() ,
уменьшающие
,
уменьшающие
![]() .
.
6. Определим первое приближение для управляющих воздействий
![]()
7. Интегрируя
уравнения (3.133), (3.134), находим первое
приближение для фазовых координат
![]() .
.
Вычисляем значения функционалов (3.144) при управляющих воздействиях и фазовых координатах первого приближения, т.е.
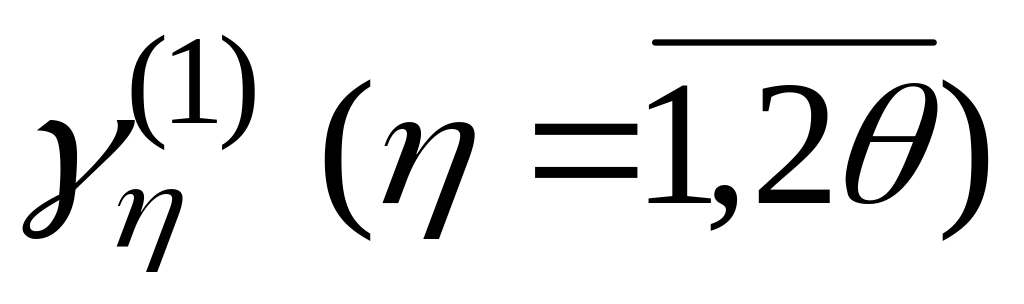 .
Если для всех
.
Если для всех
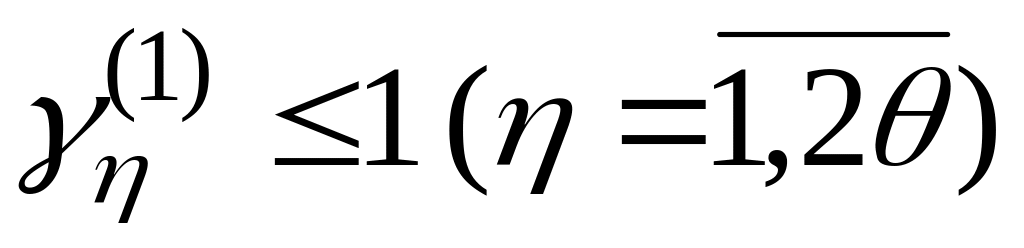 ,
то в силу выполнения условия
,
то в силу выполнения условия
 задача проектирования решена, если же
хотя бы для одного индекса
задача проектирования решена, если же
хотя бы для одного индекса
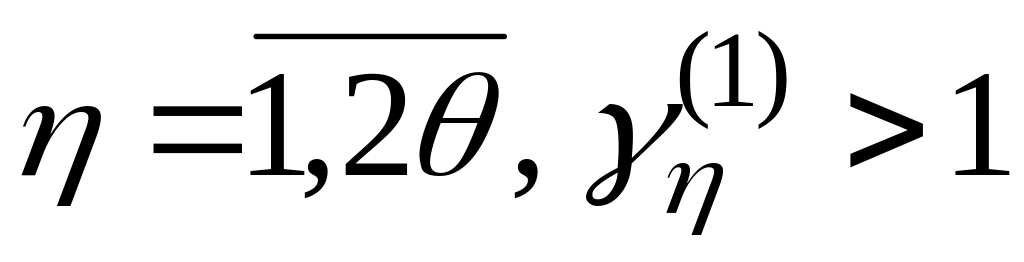 ,
то описанную процедуру надо повторить,
начиная с п.3 .
,
то описанную процедуру надо повторить,
начиная с п.3 .
Доказательства теорем, утверждений и следствий, приведенных в данной главе, можно найти в работах [3, 10, 11, 17].
Г Л А В А IV
