3.2.5. Распределение ограничений на проектные параметры

целевых подсистем

Как уже отмечалось, для каждой целевой подсистемы формируется и решается две задачи: построение областей допустимых вариаций проектных параметров и распределение ограничений на параметры системы – показатели качества функционирования подсистемы нижнего уровня. Последняя задача является ключевой при аналитическом проектировании многоуровневых систем.

Если первая задача требует выделения некоторого множества в пространстве параметров, для которых заведомо выполняются ограничения на качество функционирования целевой подсистемы, то вторая, помимо первого условия, накладывает определенные ограничения на саму структуру области допустимых вариаций, то есть должна быть определена в виде системы независимых ограничений на вариации каждого проектного параметра в отдельности. Геометрически задача распределения ограничений трактуется как задача вписания в область допустимых вариаций параметров m-мерного параллелепипеда с гранями, параллельными координатным плоскостям. Ребра параллелепипеда определяют ограничения на каждый из проектных параметров целевой подсистемы.

Постановка задачи. Особенностью задачи распределения ограничений является ее некорректность [3]. При распределении ограничений обычно стараются максимизировать их по каждому из проектных параметров при сохранении показателей качества функционирования целевой подсистемы в заданных пределах. Однако достичь одновременно максимальных ограничений невозможно и, следовательно, необходим поиск их компромиссных значений.

С учетом изложенного, задачу распределения ограничений на проектные параметры целевой подсистемы можно представить в виде:

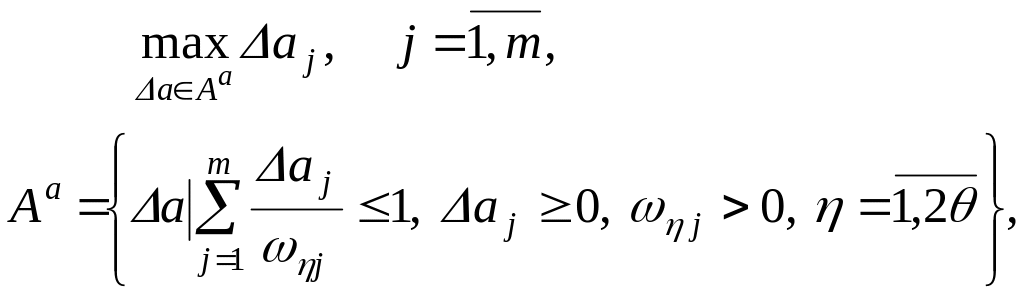(3.79)

где – множество, аппроксимирующее симметричную область допустимых вариаций параметров .

Задача (3.79) – типичная задача многокритериальной оптимизации с положительными линейными ограничениями, характерной особенностью которой является совпадение пространства критериальных функций с пространством переменных.

Для решения задачи (3.79) применим минимаксный подход, который в нашем случае сводится к решению следующей задачи

(3.80)

Алгоритм численного решения. Для решения задачи распределения ограничений на проектные параметры целевой подсистемы в виде (3.80), необходимо осуществить следующую последовательность операций.

1. Номинальные значения проектных параметров

и соответствующие им значения критериев качества целевой подсистемы предполагаются известными в результате предварительных исследований.

2. Вычисляются все производные от функционалов качества по каждому проектному параметру в точке , то есть

.

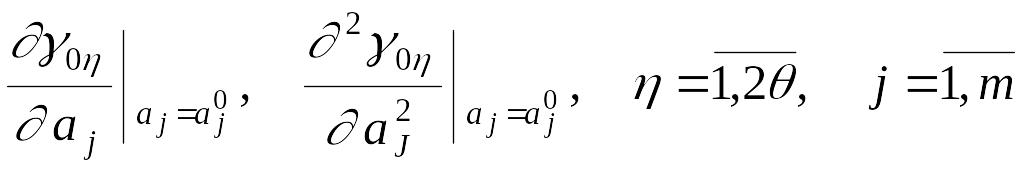3. Задаемся произвольными положительными вариациями проектных параметров 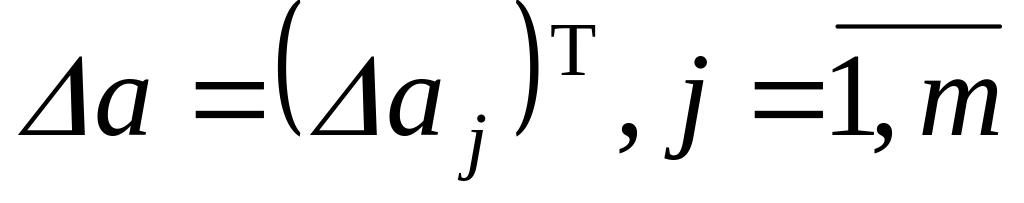, и вычисляем значения всех функционалов для каждой вариации, то есть

, .

4. В зависимости от знака производных 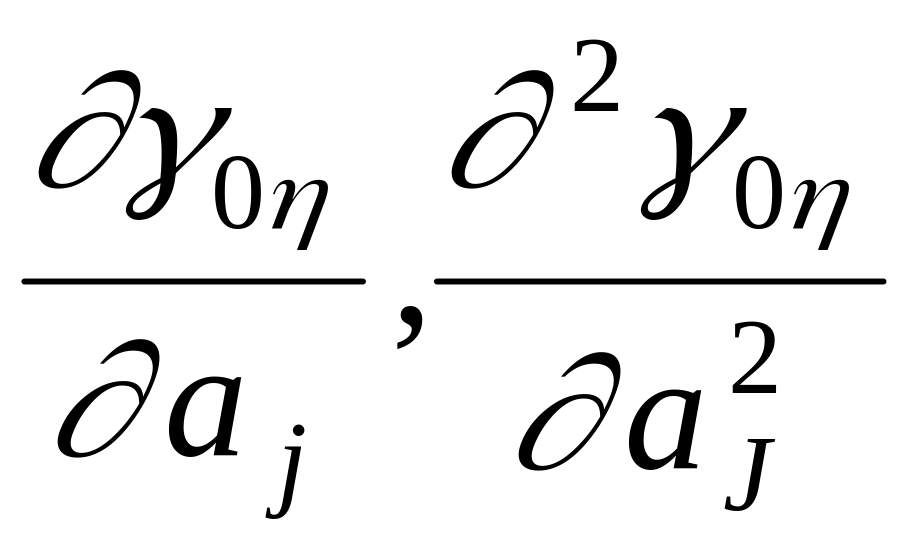и численных значений функционалов выбираем по формулам (3.73), (3.74) форму записи соответствующего компонента вектора .

5. Полагая , определяем методом итераций такие вариации , при которых функционалы качества функционирования целевой подсистемы находятся на границе области допустимых значений, то есть .

6. Корректируем найденные вариации так, чтобы выполнялось условие

7. Формируем матрицы , осуществляя при этом для каждого вектора вычисления с п.3 по п.6 .

8. Затем, для каждой j-й вариации проектного параметра , выбираем минимальные по абсолютной величине коэффициенты по индексу , то есть

9. В заключение алгоритма, решаем следующую задачу максимизации

В результате получаем вписанный в область допустимых изменений проектных параметров m-мерный брус, каждая грань которого определяет диапазон независимого изменения

Примечание. При решении задач как аппроксимации областей допустимых вариаций проектных параметров, так и распределения ограничений на проектные параметры целевых подсистем, необходимо уметь вычислять как показатели качества, так и их производные по параметрам. Если явная функциональная зависимость показателей качества от параметров неизвестна, то конкретные показатели и их производные по параметрам вычисляются путем моделирования функционирования разрабатываемой подсистемы на ЭВМ. В том же случае, когда показатели качества представляют собой скалярную функцию от функций состояния подсистемы и управляющих параметров, то для вычисления градиентов функционалов или производных по параметрам удобно использовать метод функций чувствительности.

Пусть, например, поведение целевой подсистемы описывается уравнениями (3.35), (3.36), которые зависят только от управляющих параметров . Дифференцируя эти уравнения по параметрам и вводя обозначения

(3.81)

получим следующую систему уравнений для определения функций чувствительности :

(3.82)

где

(3.83)

Тогда для вычисления производных по параметрам от целевых функционалов имеем следующее выражение:

(3.84)

где производные , вычисляются аналитически, а функции чувствительности находятся из решения системы дифференциальных уравнений (3.82) (3.83).