Глава 9. Вихревое течение идеальной несжимаемой жидкости.

Вихревым называется движение жидкости, сопровождающееся вращением частиц вокруг своих осей. Вихревому движению в пространстве можно поставить в соответствие систему вихревых линий. Вихревая линия -это огибающая векторов мгновенной угловой скорости. Вектор угловой скорости перпендикулярен плоскости вращения жидкой частицы, так что из конца вектора вращение наблюдается против часовой стрелки. Так как вектор угловой скорости в каждой точке направлен по мгновенной оси вращения частицы, то вихревая линия может быть представлена как воображаемая мгновенная криволинейная ось вращения группы частиц. Вихревые линии в общем случае не совпадают с линиями тока и могут пересекаться с ними. Дифференциальным уравнением вихревой линии является условие коллинеарности касательной к вихревой линии и вектора угловой скорости жидкой частицы в данной точке.

dx/_x = dy/_y = dz/_z

Напряжением или интенсивностью вихревой трубки называется удвоенное произведение угловой скорости вращательного движения на площадь поперечного сечения трубки dI = 2 dF

И нтенсивность вихревой трубки является мерой завихрения жидкости, содержащейся в ней. Интенсивность вихревого шнура, скорость вращения частиц в сечении которого переменна, определится выражением:

Аналогом уравнения неразрывности в вихревом движении жидкости является теорема Гельмгольца: интенсивность вихревого шнура на всём его протяжении постоянна, то есть: F = const (167)

По существу теорема Гельмгольца выражает условие сплошности среды и справедлива для любой сплошной среды независимо от её физических свойств при условии, что поле скоростей является непрерывной функцией координат.

Уравнение [167] отражает условие неразрывности вихрей. Действительно, если предположить, что у вихревого шнура в некоторой точке площадь поперечного сечения равна нулю, то согласно теореме Гельмгольца в этой точке угловая скорость вращения жидкой частица бесконечно велика, что противоречит физическим представлениям. Поэтому вихрь нигде не может оборваться в жидкости, он может опираться на твердую поверхность, свободную поверхность жидкости, а внутри жидкость может сворачиваться в кольцо. Таким образом, теорема Гельмгольца налагает определенные ограничения на форму вихрей в идеальной жидкости.

Наряду с интенсивностью вихревой нити вихревое движение характеризуется циркуляцией скорости. Циркуляцией скорости Г по замкнутому контуру L называется интеграл от скалярного произведения векторов с и dS, взятый по всему контуру.

Вектор элемента дуги dS направлен по касательной к контуру, так что обход контура по направлению вектора dS происходит против часовой стрелки.

В потенциальном потоке идеальной несжимаемой жидкости циркуляция скорости по любому контуру тождественно равна нулю.

Д ействительно:

Однако обратное утверждение (если циркуляция скорости по какому-либо контуру равна нулю, то течение потенциально) несправедливо. И в самом деле, можно представить вихревое течение, образованное парой вихрей одинаковой интенсивности, но разного знака. Циркуляция по контуру, охватывающему оси вихрей, в этом случае равна нулю.

Ц иркуляция скорости и интенсивность вихря непосредственно связаны между собой: циркуляция скорости по произвольному замкнутому контуру равна потоку вектора вихря через поверхность, ограниченную этим контуром, или сумме интенсивностей всех вихревых нитей, пересекающих эту поверхность (такая формулировка известна как теорема Стокса). Теорему Стокса легко доказать для элементарного контура размерами dx, dy (рис.30). Пусть скорость на отрезке ОС; – u, тогда скорость на отрезке АВ:

С оответственно, если скорость на отрезке ОА- v, то скорость на отрезке ВС:

z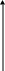

z

v

A

u

dyz

O

y

dz

C

u+ u dy

y

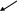
B

x

v+v dx

x

Рис.30. К расчету циркуляции скорости по элементарному контуру.

Таким образом, циркуляция скорости по замкнутому контуру, охватывающему трубку, равна напряжению вихревой трубки. Циркуляция же по контуру, лежащему на поверхности вихревой трубки, но не охватывающему трубку, равна нулю.

Вихрь в идеальной жидкости может быть представлен как масса жидкости, заключенная внутри вихревого шнура, вращающаяся по закону твердого тела. Действительно, при рассмотрении циркуляционного безвихревого течения была выявлена особая зона в окрестности начала координат. При этом кинематические граничные условия на радиусе особой зоны r_a для идеальной жидкости выполняются и в том случае, если среда, заполняющая пространство внутри цилиндра радиуса r_a, вращается с произвольной угловой скоростью  вокруг оси Z. C_ = r_a (167)

С о стороны потенциального движения на радиусе особой зоны скорость определится по известному потенциалу скорости.

Поэтому: r_a = Q /2r_a ; Q = 2r_a²= I = Г

Таким образом, в потенциальном безвихревом течении величина Q является физически циркуляцией скорости по любому контуру, охватывающему начало координат, Циркуляция же скорости по любому контуру, не охватывающему начала координат, равна нулю.

Согласно уравнению (167) скорость жидкости внутри вихря возрастает пропорционально радиусу, а вне вихря, согласно уравнению (168),убывает обратно пропорционально радиусу.

В этом смысле можно утверждать, что прямолинейный вихрь наводит (индуцирует) в окружающей среде определенное поле скоростей. Если вихрь имеет сложную геометрическую форму, то величину скорости, индуцируемую в какой-либо точке, отстоящей на расстояние r от оси вихря, от участка вихря длинной dL можно определить по формуле Био - Савара. dc = Гsin dL/4r²

В последней формуле  - угол, под которым виден участок вихря длинной dL из рассматриваемой точки, Г - циркуляция скоростей по любому контуру, охватывающему вихрь.

Для идеальной жидкости справедлива теорема Томсона: если внешние массовые силы, действующие в идеальной жидкости, потенциальны, то циркуляция скорости по любому замкнутому контуру постоянна во времени. Иначе говоря, в идеальной несжимаемой жидкости с консервативными массовыми силами безвихревое движение этой жидкости, зафиксированное в какой -либо момент времени, так и останется безвихревым в последующем, что эквивалентно утверждению о вечности вихрей.

Циркуляционное вихревое движение ( вихрь ) реализуется и в том случае, если внутри некоторого цилиндра радиуса r_a находится твердое тело, вращающееся с некоторой угловой скоростью . Это циркуляционное обтекание цилиндра. Циркуляционное обтекание цилиндра, как потенциальное течение, получается сложением простых потенциальных течений : параллельного потока и диполя, дающих бесциркулярное обтекание цилиндра, с циркуляционным течением, вызванным вихрем, ось которого совпадает с осью цилиндра. В частности представляет интерес поперечное обтекание цилиндра вихрем с отрицательной циркуляцией. В этом случае.

 = u (1 + r_²/ r² ) r Cos - Г  / 2

 = u (1 – r_²/ r² ) r Sin - Г lnr / 2

Из выражения для функции тока видно, что наложение циркуляционного потока (вихря) нарушает симметрию линий тока относительно горизонтальной оси. Действительно, окружная и радиальная составляющие скорости определяются из выражения для потенциала скоростей.

При этом на поверхности цилиндра: Cr = 0; C_ = -2 uSin - Г/2r_

В точках торможения потока: Sin_ = – Г/4r_u; _ = arcSin (– Г/4r_u )

Таким образом, при условии – Г  4r_u; /2 _ 3/2; 3/2  _ 2

Если – Г > 4r_u, то точки полного торможения потока расположены вне цилиндра, соответственно и нулевая линия тока находится вне цилиндра. Между поверхностью цилиндра и нулевой линией тока жидкость движется по замкнутым, хотя и не концентрическим траекториям.

Х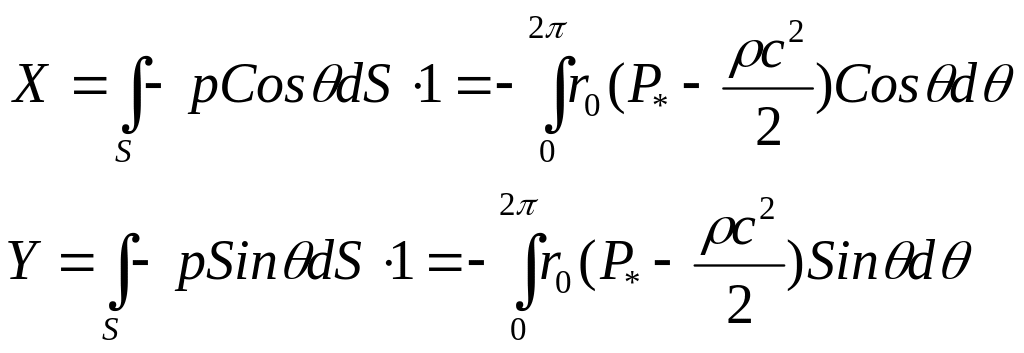 арактерной особенностью циркулярного обтекания цилиндра является симметричность поля скоростей (и следовательно давлений) относительно оси Y и отсутствие симметрии относительно оси Х. В связи с этим следует ожидать наличия равнодействующей сил давления вдоль оси Y. Действительно,

Поскольку C = C_ = -2 uSin - Г/2r, то X = 0, Y = uГ

Последний результат есть содержание теоремы Жуковского: подъемная сила, возникающая при обтекании цилиндра идеальной несжимаемой жидкостью, равна произведению скорости натекающего потока на его плотность и на циркуляцию скорости по любому контуру, охватывающему цилиндр. Методами конформных преобразований можно показать, что теорема Жуковского справедлива при обтекании произвольного тела потенциальным потоком идеальной несжимаемой жидкости.

Из теоремы Жуковского следует, что для получения подъемной силы тела произвольной формы, обтекаемого плоскопараллельным потенциальным потоком, необходимо обеспечить такое поле скоростей, при котором циркуляция скорости по любому контуру, охватывающему тело, должна быть отлична от нуля. Для кругового цилиндра, обтекаемого вязкой жидкостью, этого можно достичь путем вращения цилиндра.

Согласно теореме Жуковского каждому значению циркуляции, характеризующей поле скоростей вокруг обтекаемого тела, соответствует определенное значение подъемной силы.

Задавая различные значения циркуляции, можно получить разные распределения линий тока вокруг обтекаемого тела и соответственно отличающиеся между собой значения подъемной силы. Таким образом, теорема Жуковского не дает однозначного ответа на вопрос о величине подъемной силы, поскольку при обтекании потенциальным потоком произвольного тела заранее не известно распределение линий тока вокруг тела и, следовательно, не известна величина циркуляции скорости. Поэтому, задавая произвольные значения циркуляции, можно получить ряд значений подъемной силы и каждый такой случай теоретически вполне возможен. Поэтому при практическом применении требуется своего рода граничное условие, которое из множества возможных случаев оставляло бы одно. Чаплыгин впервые обратил внимание на то, что для любого обтекаемого тела характерно положение задней точки торможения потока до нулевой скорости. Было замечено, что при обтекании тел с острой задней кромкой задняя точка торможения совпадает с угловой точкой задней кромки. Методами конформных преобразований можно показать, что если бы точка торможения не совпадала бы с угловой точкой задней кромки, то вблизи нее скорость обтекания была неограниченна, что противоречит физическим представлениям. Такого рода граничное условие сформулировано в виде постулата Жуковского-Чаплыгина: при обтекании тела с острой задней кромкой физически реализуется такое единственное значение циркуляции, при котором задняя точка полного торможения потока совпадает с задней кромкой.