
- •Рыбинская государственная авиационная технологическая академия Конспект Лекций по механике жидкости и газа
- •Оглавление
- •Введение Общая постановка задач в механике жидкости и газа.
- •Кинематические понятия и определения, используемые в прикладной гидрогазодинамике.
- •Классификация сил, действующих в жидкости при ее движении.
- •Глава 1. Одномерное энергоизолированное установившееся движение легкой идеальной жидкости.
- •1.1. Уравнение движения
- •Лёгкой идеальной жидкости в элементарной струйке тока.
- •1.2. Интегрирование уравнения движения.
- •1.3. Скорость звука
- •В элементарной трубке тока
- •1.4. Связь между формой струйки тока и величиной скорости сжимаемого газового потока, движущегося в условиях энергетической изолированности.
- •1.5. Вычисление массового расхода газа по параметрам торможения и приведенной скорости потока. Газодинамические функции расхода.
- •1.6. Газодинамический импульс. Газодинамические функции импульса.
- •Глава 2. Установившееся одномерное движение вязкого сжимаемого газа в канале переменного сечения при наличии энергообмена и массообмена с окружающей средой.
- •Глава 3. Одномерное установившееся движение вязкой жидкости в каналах постоянного сечения.
- •3.1. Описание турбулентных течений путем использования осредненных во времени величин
- •Степень турбулизации течения определяется интенсивностью турбулентности
- •3.2. Гипотеза турбулентности л. Прандтля. Понятие о длине пути перемешивания. Логарифмический профиль осредненной скорости.
- •3.3. Гидравлическое сопротивление круглых труб.
- •3.4. Гидравлические потери на местных сопротивлениях.
- •3.5. Взаимодействие потоков вязких жидкостей. Перемешивание газовых потоков. Потери смешения.
- •Глава 4. Движение вязкой жидкости вблизи твердой поверхности.
- •4.1. Пограничный слой.
- •Т аким образом:
- •4.2. Физическая толщина пограничного слоя. Интегральные толщины.
- •4.3. Интегральное соотношение для пограничного слоя
- •4.4. Методы расчёта пограничного слоя при наличии продольного градиента давления
- •Глава 5. Осреднение параметров газового потока.
- •Глава 6. Сверхзвуковое течение газа.
- •С пониженным давлением.
- •Глава 7. Основные уравнения в механике жидкости и газа.
- •7.1. Уравнение неразрывности.
- •7.2. Уравнение движения.
- •7.3. Дифференциальные уравнения движения.
- •При этом в силу равновесия элемента имеет место равенство моментов сил
- •7.4. Дифференциальные уравнения Навье-Стокса.
- •7.5. Уравнение энергии.
- •7.6. Дифференциальное уравнение энергии.
- •7.7. Дифференциальные уравнения Эйлера.
- •2 .Стационарное винтовое течение:
- •Глава 8. Потенциальное движение идеальной жидкости.
- •Глава 9. Вихревое течение идеальной несжимаемой жидкости.
- •Глава 10. Основы теории подобия
- •Глава 11. Связь энтропии газового потока с коэффициентом сохранения полного давления.
Глава 6. Сверхзвуковое течение газа.
Сверхзвуковые течения идеального газа отличаются от дозвуковых тем, что зона возмущений (при распространении слабых возмущений) ограничена в пространстве. Действительно, пусть в какой-то момент времени (рис.12.) в точке А возникло малое возмущение. Это возмущение за время dt распространится в сфере радиусом α dt.

Рис.12. Распространение слабых
возмущений в сверхзвуковом потоке
П![]() ри
этом центр возмущённой области сместится
на расстояние c
dt [c > a ]
вследствие движения потока.
В итоге
область возмущённых параметров
ограничится конусом с углом полураствора
.
ри
этом центр возмущённой области сместится
на расстояние c
dt [c > a ]
вследствие движения потока.
В итоге
область возмущённых параметров
ограничится конусом с углом полураствора
.
В
(125)
В течениях с непрерывным увеличением скорости [рис.13] происходит расширение газа до давления окружающей среды [в соответствии с необходимостью соблюдения граничного условия] последовательно и непрерывно на системе конусов, имеющих общую вершину А.
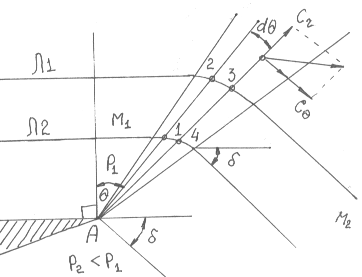
Рис.13. Истечение сверхзвукового потока в область
С пониженным давлением.
При этом поток поворачивает в сторону области пониженного давления на угол . Первый конус возмущений наклонён по отношению к первоначальному вектору скорости на угол 1 = arcSin ( 1 / M1 ).
Последний конус возмущений имеет угол полураствора по отношению к конечному вектору скорости 2 = arcSin ( 1 / M2 ). Поскольку процесс расширения газа на каждом конусе является изоэнтропическим, то и процесс расширения на всей совокупности конусов [на волне разрежения] также является изоэнтропическим. Это означает, что полное давление сохраняется постоянным на линии тока, пересекающей волну разрежения.
Для расчёта параметров газа на линии тока, пересекающей волну разрежения, и для расчёта ориентации и угловой протяжённости волны разрежения, необходимо иметь соответствующие уравнения, которые могут быть получены из интеграла уравнения движения для идеального сжимаемого газа.
![]()
И
(126)
С![]()
![]() вязь
между составляющими C
и Сr обнаруживается из следующей операции
(Рис.13):
при обходе по контуру 12341, образованному
линиями тока Л1 и
Л2 и секущими
двух конусов, отстоящих друг от друга
на малое угловое расстояние d,
перемножаются проекции скорости на
соответствующие длины сторон контура
и затем алгебраически складываются
(определяется
циркуляция скорости по контуру 12341).
Поскольку поток безвихревой до волны
разрежения, безвихревой и после волны
разрежения, то естественно поток должен
быть безвихревым и в волне разрежения.
Пусть составляющие скорости на конусе
12 есть Cr и C.
Тогда составляющие скорости на конусе
43 есть: Cr + (dCr/d
)
dи
C
+(dC/d)
d.
Пусть расстояние точки 1 от вершины А
равно r. Тогда расстояние точки 2 от
вершины А есть r + dr. В результате вычисления
циркуляции получается следующее
соотношение:
вязь
между составляющими C
и Сr обнаруживается из следующей операции
(Рис.13):
при обходе по контуру 12341, образованному
линиями тока Л1 и
Л2 и секущими
двух конусов, отстоящих друг от друга
на малое угловое расстояние d,
перемножаются проекции скорости на
соответствующие длины сторон контура
и затем алгебраически складываются
(определяется
циркуляция скорости по контуру 12341).
Поскольку поток безвихревой до волны
разрежения, безвихревой и после волны
разрежения, то естественно поток должен
быть безвихревым и в волне разрежения.
Пусть составляющие скорости на конусе
12 есть Cr и C.
Тогда составляющие скорости на конусе
43 есть: Cr + (dCr/d
)
dи
C
+(dC/d)
d.
Пусть расстояние точки 1 от вершины А
равно r. Тогда расстояние точки 2 от
вершины А есть r + dr. В результате вычисления
циркуляции получается следующее
соотношение:
Полученное уравнение приводится к виду: C = dCr/d (127)
Это и есть уравнение связи между составляющими скорости Cr и C.
Т
(128)
И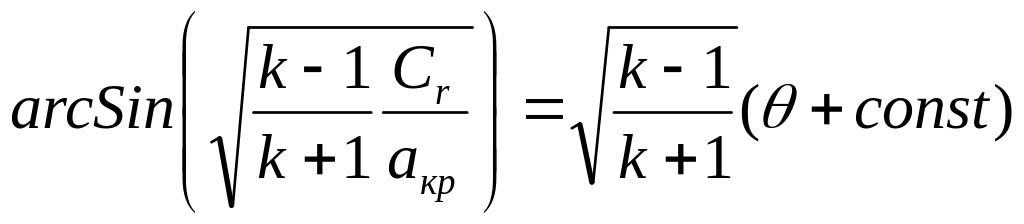 нтеграл
уравнения [128]:
нтеграл
уравнения [128]:
П
(129)![]() остоянную
интегрирования,
вообще говоря, следует
определять из граничных условий для
конкретной задачи, однако есть смысл
вычислить её для случая
= 1. При этом const = 0, а интеграл имеет
наиболее простой вид:
остоянную
интегрирования,
вообще говоря, следует
определять из граничных условий для
конкретной задачи, однако есть смысл
вычислить её для случая
= 1. При этом const = 0, а интеграл имеет
наиболее простой вид:
Угол отсчитывается от нормали к вектору скорости, равной скорости звука. В этом случае рассматривается расширение потока, движущегося со скоростью звука. Расширение потока, движущегося с произвольной сверхзвуковой скоростью, следует рассматривать как мысленное от критического состояния до данной скорости и далее как реальное в соответствии с поставленной задачей.
В соответствии с уравнением (127):
В
(130)![]()
![]() результате:
результате:
Максимальный угол в волне разрежения, соответствующий истечению в вакуум, определится из уравнения [131] при 2 = (k + 1)/(k – 1)
![]()
П

 ри
этом последний конус возмущений
вырождается в луч, направленный вдоль
линии тока. Действительно, при
(k + 1)/(k –
1); M
.
ри
этом последний конус возмущений
вырождается в луч, направленный вдоль
линии тока. Действительно, при
(k + 1)/(k –
1); M
.
![]()
Максимально возможному расширению потока до нулевого давления [истечение в вакуум] соответствует максимальное отклонение потока от первоначального направления. Как видно из рис.13, справедливо тригонометрическое уравнение:
+ = + /2 (132)
П![]() оэтому
оэтому
Возможно графическое представление уравнений, описывающих непрерывное расширение сверхзвукового потока в форме годографа скорости и диаграммы характеристик. Под годографом скорости понимается кривая, описываемая концом вектора скорости при его повороте и увеличении модуля, что соответствует расширению газа от критического давления до нулевого. При этом модуль скорости увеличивается от 1 до (k + 1)/(k – 1), а угол поворота потока
о
![]() т
0 до .
т
0 до .
Кривая годографа скорости относится к классу эпициклоид. Семейство годографов скорости, смещённых друг по отношению к другу на определенное угловое расстояние и ориентированных во взаимно противоположных направлениях образует диаграмму характеристик весьма удобную для расчетов, что позволяет обойтись без вычислений по соответствующим уравнениям.
П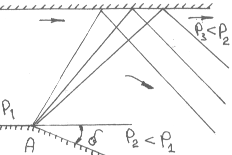 ри
распространении волны разрежения на
твердую поверхность происходит ее
отражение с сохранением знака,
т.е. волна
разрежения отражается от твердой
поверхности как волна разрежения ( Рис.
14 ).
ри
распространении волны разрежения на
твердую поверхность происходит ее
отражение с сохранением знака,
т.е. волна
разрежения отражается от твердой
поверхности как волна разрежения ( Рис.
14 ).
Рис. 14. Отражение волны разрежения от твёрдой поверхности.
Дело в том, что в волне разрежения поток поворачивается на некоторый угол, в то время как граничное условие для идеальной жидкости на твердой поверхности предполагает параллельность вектора скорости стенке. Поэтому в месте падения каждого конуса волны на твердую поверхность в силу соблюдения граничного условия происходит поворот потока в сторону противоположную первоначальному повороту. Этому соответствует расширение потока до давления меньшего, чем давление за первичной волной разрежения. В результате возникает отраженная волна разрежения.
При распространении волны разрежения на границу струи идеального газа (за границей струи выше линии B – B газ неподвижен) происходит ее отражение с переменой знака, т.е. волна разрежения отражается от границы струи как волна сжатия (рис.15).

Рис. 15. Отражение волны разрежения от границы струи.
В месте соприкосновения первичной волны разрежения с границей струи происходит снижение давления в потоке, в то время как вне струи давление постоянно и совпадает с давлением на границе струи. Поэтому в месте падения волны разрежения на границу струи в силу соблюдения граничного условия происходит сжатие потока до первоначального давления. Этому соответствует сжатие потока до первоначального давления и его дальнейший поворот. В результате возникает отраженная волна сжатия.
Распространение конечных возмущений в сверхзвуковом потоке в виде повышения давления на конечную величину не может происходить плавно и изоэнтропически.

Рис. 16. Образование скачка уплотнения при обтекании внутреннего тупого угла.
В самом деле, при обтекании внутреннего тупого угла сверхзвуковым потоком (Рис.16) плавное изоэнтропическое торможение в системе конусов возмущений означало бы, что каждый последующий конус (по мере сжатия потока) имел бы большой угол полураскрытия, чем предыдущий в связи с уменьшением скорости потока, что противоречит логике. Между тем задача о торможении сверхзвукового потока поставлена корректно и единственное возможное преодоление логического противоречия состоит в том, что имеет место скачкообразное торможение сверхзвукового потока на некоторой поверхности, занимающей промежуточное положение между конусами возмущений по начальной (линия AB на рис.16.) и конечной (линия AC на рис.16.) скорости. Скачкообразное торможение на некоторой поверхности можно представлять как ударный процесс, в ходе которого терпят разрыв все кинематические и газодинамические параметры потока (кроме температуры торможения, которая постоянна в силу энергетической изолированности течения ).
П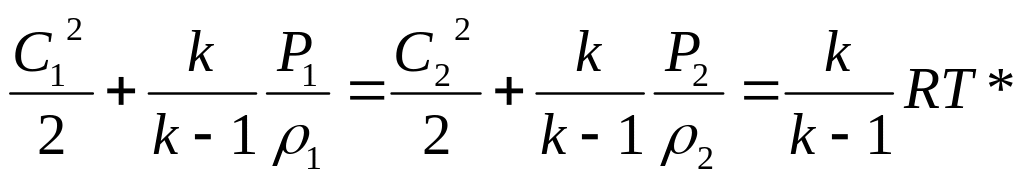 ри
этом на скачке уплотнения соблюдаются
все законы механики,
что и даёт
возможность рассчитывать течение газа.
Так, в частности закон сохранения энергии
при энергоизолированном движении
идеального газа в скачке уплотнения
имеет вид : i* = const, что эквивалентно
уравнению:
ри
этом на скачке уплотнения соблюдаются
все законы механики,
что и даёт
возможность рассчитывать течение газа.
Так, в частности закон сохранения энергии
при энергоизолированном движении
идеального газа в скачке уплотнения
имеет вид : i* = const, что эквивалентно
уравнению:
В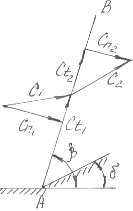 этом уравнении индексом 1 обозначены
параметры потока до скачка,
индексом
2-параметры потока после скачка (рис.17)
этом уравнении индексом 1 обозначены
параметры потока до скачка,
индексом
2-параметры потока после скачка (рис.17)
Рис.17. Схема течения газа в скачке уплотнения.
Имеет смысл скорость потока представить в виде геометрической суммы двух составляющих: скорости Сn - направленной перпендикулярно фронту скачка и скорости C - направленной по фронту скачка.
Закон сохранения массы может быть сформулирован как условие равенства массовых расходов через единичную площадку, перпендикулярную фронту скачка.
1Cn1 = 2Cn2
Закон сохранения количества движения в проекции на направление скачка (на плоскость скачка) имеет вид: 1Cn1(Ct1 – Ct2 ) = 0
Из этого уравнения в частности следует что Ct1 = Ct2, т.е. тангенциальные составляющие скорости на скачке не меняются. Вывод очевиден в связи с отсутствием импульса сил на направление скачка.
Закон сохранения количества движения в проекции на нормаль к плоскости скачка имеет вид: 1Cn1(Cn1 – Cn2 ) = P2 – P1
Для установления связи между составляющими скорости на скачке из системы уравнений механики следует исключить плотность и давление, имея в виду, что температура торможения связана с критической скоростью. В итоге получается основное кинематическое соотношение для скачка уплотнения.
Cn1 Cn2 = a кр2 – Ct2 ( k – 1 )/(k + 1) (133)
B безразмерной форме это же соотношение записывается в виде :
n1 n2 = 1 – t2 ( k – 1 )/(k + 1)
Из уравнения (133) в частности следует, что если = /2 [ прямой скачёк ], то Ct = 0; Cn1 = C1; Cn2 = C2 и справедливо соотношение: 1 2 = 1
Из этого соотношения следует, что: 2 = 1/1
Поскольку изначально поток сверхзвуковой, то 1 >1, а 2 < 1. Это означает, что за прямым скачком скорость всегда дозвуковая. Это наиболее сильный скачёк из всех возможных при прочих равных условиях.
Из уравнений сохранения массы, количества движения и энергии путём исключения соответствующих величин вытекают соотношения, связывающие параметры состояния в скачке, скорости и угол поворота потока с углом фронта скачка.

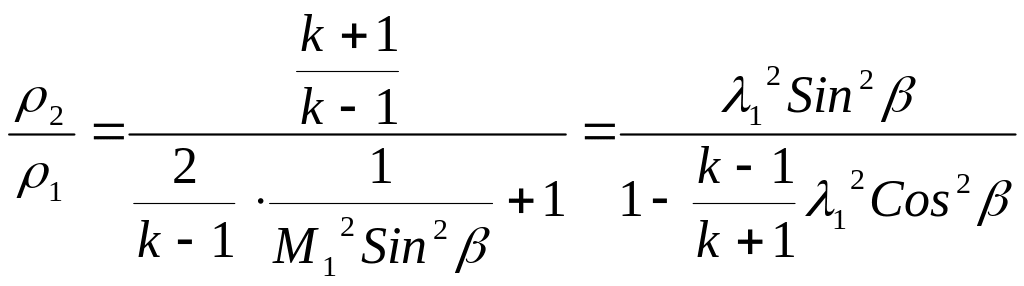
В
прямом скачке уплотнения =
/2,
поэтому: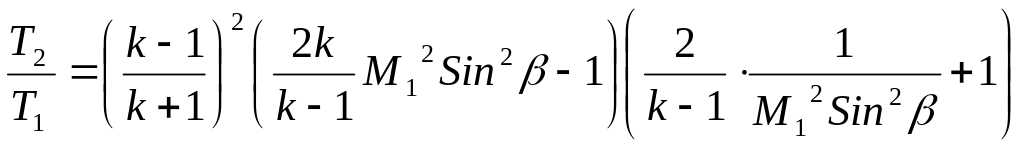
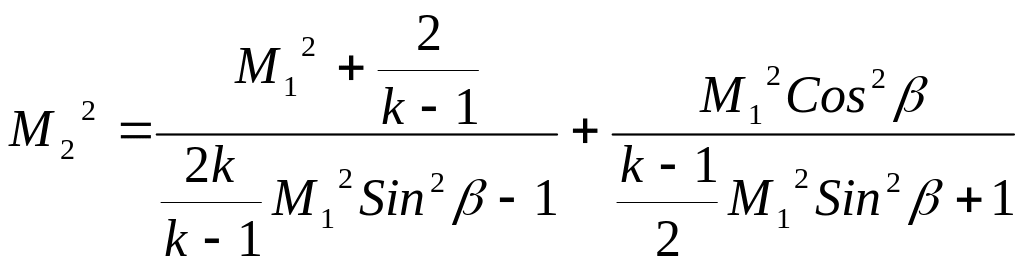



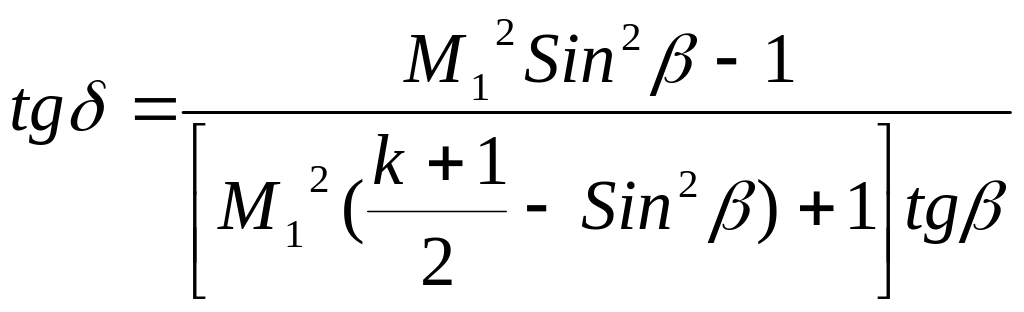
И з последних уравнений отчётливо видно, что при неограниченном увеличении числа Маха перед скачком неограниченно возрастают давление и температура за скачком, в то время как плотность за скачком возрастает несущественно. Действительно, при M1 , 1= (k + 1)/(k – 1), 2 1 (k + 1)/(k – 1).
В то же время, если бы было возможно плавное торможение потока, сопровождающееся изоэнтропическим процессом сжатия газов, то при M1 все параметры состояния [в том числе и плотность] возрастали бы неограниченно по отношению к параметрам перед скачком.
Причиной отмеченного является неограниченный рост энтропии газа при неограниченном возрастании интенсивности скачка, что является следствием необратимого перехода части механической энергии газа в тепловую на фронте скачка из - за неупругого удара молекул газа.
Действительно, в энергоизолированном процессе прирост энтропии определится из уравнения: dS = [R k / (k-1) ] dT /T – R dP /P
Согласно уравнению состояния газа: dT / T =dP / P – d /
Поэтому dS = [ R / (k-1) ] ( dP / P – k d / )
S1 – 2 = [ R / ( k – 1)] ln ( P2 / P1) ( 1 / 2 )k
Поскольку при M1 ; P2 / P1 , а ( 1 / 2 )k [ (k-1) / (k+1) ] k, то S1 – 2 .
К стати,
из уравнений
связывающих давления и плотности на
прямом скачке следует уравнение ударной
адиабаты:
стати,
из уравнений
связывающих давления и плотности на
прямом скачке следует уравнение ударной
адиабаты:
В изоэнтропийном же процессе эти параметры связаны иным образом:
P / k = const или P2 / P1 = ( 2 / 1 )k
Однако в случае очень слабого скачка уравнение ударной адиабаты переходит в уравнение изоэнтропы и прирост энтропии стремится к нулю. Действительно, в случае слабого скачка: P2 = P1 + dP, 2 = 1+ d. Поэтому уравнение ударной адиабаты записывается в виде: dP / P = k d /
Интеграл этого уравнения: P/k = const
З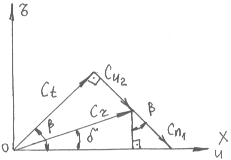 ависимости
между параметрами потока на скачке
уплотнения можно представить графически,
составив уравнение годографа скорости
[уравнение ударной поляры]. Для этого в
прямоугольной системе координат ХОУ
скорость перед скачком следует направить
по оси Х, составив зависимость между
вертикальной составляющей скорости за
скачком v
и горизонтальной составляющей u
(рис.18).
ависимости
между параметрами потока на скачке
уплотнения можно представить графически,
составив уравнение годографа скорости
[уравнение ударной поляры]. Для этого в
прямоугольной системе координат ХОУ
скорость перед скачком следует направить
по оси Х, составив зависимость между
вертикальной составляющей скорости за
скачком v
и горизонтальной составляющей u
(рис.18).
Рис.18. К выводу уравнения ударной поляры
При этом Cn1 = C1Sin ; Ct = C1Cos , а основное кинематическое уравнение на скачке запишется в виде:
C![]()
![]()
![]() учётом:
учётом:
из
основного кинематического соотношения
для скачка следует уравнение для ударной
поляры .
Кривая, соответствующая полученному уравнению (рис.19), относится к классу гипоциссоид, однако в бесконечно малой окрестности точки D переходит в эпициклоиду, поскольку процесс является изоэнтропическим по причине бесконечно малого изменения первоначальной скорости. Ударная адиабата удобна для анализа и быстрого расчёта параметров потока на скачке уплотнения.
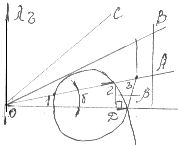
Рис.19. Ударная поляра
Действительно, скорость потока за скачком определится из пересечения секущей ОА [проведённой под углом ] с кривой [точка2]. Решения, соответствующие точкам 1 и 3 следует проигнорировать, т.к. они вступают в противоречие с физическим содержанием процесса торможения газа в скачке уплотнения. Точке 3 соответствует скачкообразное увеличение скорости и соответственно скачкообразное понижение давления [скачёк разрежения],сопровождающееся понижением энтропии газа. Между тем в энергоизолированных системах энтропия может оставаться постоянной, либо возрастать. Точке 1 соответствует снижение скорости, значительно большее, чем точке 2, и соответственно значительно больший прирост энтропии. Между тем, из двух физически возможных процессов реализуется такой, которому соответствует меньший прирост энтропии. Реализация процесса, соответствующего большему приросту энтропии, возможна при специальных условиях.
Секущая ОВ, имеющая одну точку касания с ударной полярой, определит максимально возможный угол поворота потока в косом скачке. Если секущая ОС нигде не пересекает ударную поляру, то при данных условиях [скорости потока и угла поворота] косой скачёк уплотнения вообще не реализуется.
Угол между нормалью, опущенной из точки 2 на ось абсцисс, и отрезком 2D равен углу фронта скачка.
Ступенчатое торможение сверхзвукового потока возможно в многоскачковой системе, чему соответствует обтекание некоторой ломаной поверхности. При этом может быть поставлена задача оптимизации системы скачков. Суть задачи состоит в том, чтобы подобрать углы поворота потока на отрезках ломаной т.о., чтобы суммарные потери полного давления на системе скачков были бы минимальны. Такая задача всегда разрешима.
Действительно, в двухскачковой системе, состоящей из косого скачка и последующего прямого, потери полного давления в косом скачке возрастают по мере увеличения угла фронта скачка ( рис.19a ).
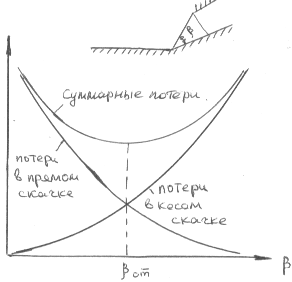
Рис.19a. Изменение потерь энергии в системе двух скачков уплотнения
При этом скорость за косым скачком уменьшается, а скорость за прямым возрастает поскольку они связаны обратной зависимостью. Таким образом интенсивность прямого скачка снижается и, соответственно, уменьшаются потери давления на прямом скачке уплотнения. Поэтому суммарные потери давления в системе из двух скачков имеют минимальное значение при некотором оптимальном значении угла фронта скачка, чему соответствует оптимальный угол поворота потока в косом скачке. В многоскачковой системе минимальные потери полного давления достигаются при равномерном торможении потока на всех скачках уплотнения.
Вообще говоря, чем больше скачков в многоскачковой системе, тем меньше потери давления на каждом скачке и меньше суммарные потери давления, поэтому возможно изоэнтропическое торможение сверхзвукового потока при обтекании вогнутой плавной поверхности. При этом геометрически гладкая образующая может рассматриваться как бесконечная совокупность системы ломаных отрезков, развёрнутых друг к другу на бесконечно малый угол. Поскольку процесс сжатия при каждом переходе от одного отрезка ломаной к другому является бесконечно слабым и, соответственно, изоэнтропическим, то и весь процесс сжатия также является изоэнтропическим. Однако изоэнтропическое сжатие возможно только для линий тока, непосредственно прилегающих к поверхности. По мере удаления от поверхности происходит наложение элементарных процессов сжатия [в связи с увеличением угла конуса возмущений по мере снижения скорости плюс увеличение наклона стенки], приводящее к возникновению прямого скачка, который наиболее интенсивный из всех возможных.
При падении скачка уплотнения на твёрдую поверхность возникает отражённый скачёк уплотнения в связи с необходимостью удовлетворения граничного условия для идеальной жидкости на твёрдой стенке. Однако при падении скачка уплотнения на свободную границу струи возникает отражённая волна разрежения в связи с необходимостью соблюдения граничного условия по давлению на границе струи.
