Глава 8. Потенциальное движение идеальной жидкости.

Безвихревое движение идеальной жидкости называется потенциальным. Необходимым и достаточным условием потенциальности течения является :

_x = _y = _z = 0

Этому соответствует определённое соотношение между частными производными составляющих скорости:

В свою очередь последние уравнения, являясь по существу условиями Коши Римана, свидетельствуют о существовании некоторой функции координат, называемой потенциалом скорости. Частные производные потенциала скорости по осям координат (x,y,z) равны соответствующим проекциям скорости:

Д ействительно, в силу отсутствия вращения частиц вокруг оси Z, например, следует:

В случае плоского (установившегося) потенциального течения при отсутствии массовых сил можно в явном виде составить уравнение для потенциала скорости. В этом случае уравнения движения (уравнения Эйлера) имеют вид:

В свою очередь согласно дифференциальному уравнению неразрывности градиенты плотности связаны со скоростями и их производными следующим образом:

П оэтому уравнение для потенциала скоростей имеет вид:

(160)

В этом уравнении обозначено: Mu = u/ ; M_v = v/. Интегрирование уравнения (160) следует проводить при граничном условии для идеальной жидкости: скорость жидкости параллельна касательной к поверхности в данной точке.

При этом следует иметь в виду, что уравнение для потенциала скорости (160) обладает различными математическими свойствами, в зависимости от скорости движения жидкости. Так, при Mu  0 и M_v  0 уравнение для потенциала скоростей переходит в уравнение Лапласа, которое классифицируется в математике как уравнение эллиптического т

(161)

ипа.

П

(162)

ри 0 < Mu <1, 0 < M_v < 1 уравнение для потенциала скоростей является уравнением параболического типа.

П ри Mu > 1; M_v > 1 уравнение для потенциала скоростей является уравнением гиперболического типа.

В

(163)

данном случае существенно, то, что общие решения уравнения какого-либо типа не могут быть общими решениями для уравнений другого типа, т.е. ситуация такова, что как будто речь идет о разных физических объектах. В действительности уравнению (161) соответствуют несжимаемые течения, уравнению (162) соответствуют сжимаемые, но дозвуковые течения, а уравнению (163) - существенно сжимаемые, сверхзвуковые течения. В каждом из этих случаев газ обладает существенно различными физическими свойствами, что и находит отражение в математическом описании модели течения.

Потенциал скорости несжимаемого течения обладает линейными свойствами в силу свойств уравнения Лапласа. Действительно, пусть имеется несколько потенциальных потоков с потенциалами скорости ₁, ₂, … _n. Тогда новая функция, полученная путем сложения потенциалов скорости исходных течений, характеризует новый потенциальный поток, проекции скорости которого равны алгебраической сумме проекций скоростей исходных потоков, т.к.:

Линейное свойство потенциала скорости исключительно важно для изучения потенциальных течений поскольку позволяет представить любое сложное течение, как сумму простейших.

Линейное свойство потенциальных течений физически обусловлено несжимаемостью жидкости. Этим же свойством обусловлено то обстоятельство, что дифференциальное уравнение неразрывности в плоских установившихся течениях идеальной несжимаемой жидкости имеет наиболее простой вид:

Последнее уравнение означает, что существует функция координат  (x, y), обладающая следующим свойством:

;

Действительно, подстановка этих соотношений в исходное уравнение дает тождество:

Ф ункция  (x, y) существует в любых течениях (в том числе и не потенциальных), т.к. ее существование вытекает из уравнения неразрывности, безусловно справедливого во всех случаях. Функция  (x, y) принимает постоянное значение для линии тока поэтому называется линией тока. Действительно, дифференциальное уравнений линий тока есть условие коллинеарности вектора скорости и касательной к линии тока:

П оэтому: ;

;

В

(164’)

потенциальных течениях несжимаемой жидкости линии тока ортогональны линиям равного потенциала (эквипотенциалям). Действительно, в потенциальных течениях _z = 0

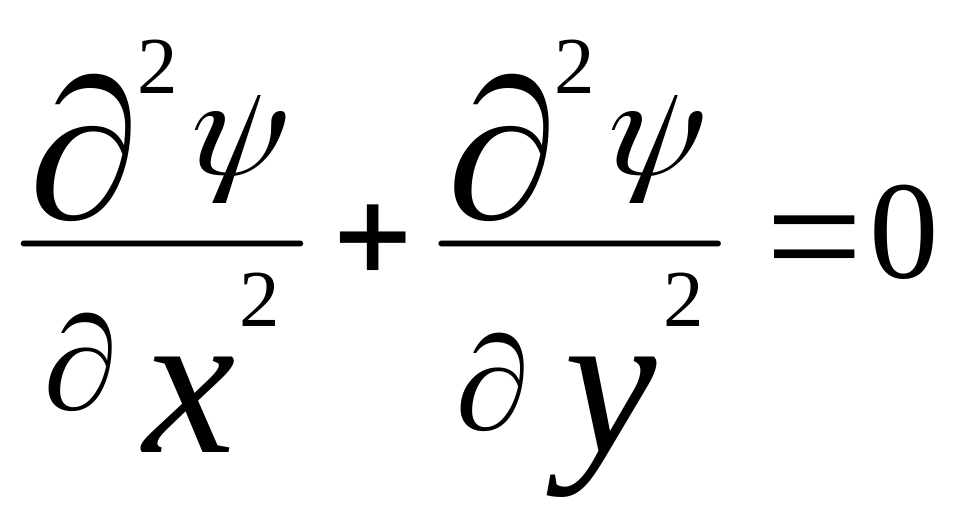
Уравнение (164) также является уравнением Лапласа. причем функция тока в уравнении (164) связана с потенциалом скорости в уравнении (162) следующим образом:

Последние уравнения являются математической формулировкой условия взаимной ортогональности в каждой точке области течения функций  ( x, y ) и  ( x, y ).

Кроме того, из факта идентичности дифференциальных уравнений для функции тока и потенциала скорости следует, что их решения взаимно заменимы. Следовательно, любому потенциальному течению можно поставить в соответствие другое потенциальное течение, линиями тока которого являются эквипотенциали исходного течения, а эквипотенциалями - линии тока исходного течения.

Следовательно, любые, как угодно сложные, потенциальные течения образованы сложением более простых течений, являющихся производными от двух простейших течений: однородного поступательного течения (плоскопараллельного потока) и источника.

Однородное поступательное течение характеризуется постоянной скоростью, направленной вдоль оси Х. Поэтому потенциал такого течения:

 = ux (164’’)

Семейство эквитенциалей - пучок прямых, параллельных оси Y.

Соответственно функция тока:  = uy. Семейство линий тока - пучок прямых, параллельных оси Х.

Источником называется поток, в котором жидкость вытекает из некоторого центра с одинаковой по всем направлениям скоростью. Поэтому линиями тока источника являются радиусы, а эквипотенциалями - окружности с центром в источнике. Действительно, объемный расход жидкости через цилиндрическую поверхность радиусом r и единичной высоты есть: Q = 2 rC.

;

(165)

Соответственно:

(166)

В уравнениях (165) и (166) r – радиус,  - угол в полярных координатах.

Источник как потенциальное течение существует везде за исключением некоторой окрестности начала координат поскольку при r  0 , C  _{ ,}   - _. Особая точка в начале координат исключается из рассмотренных путем введения некоторой области r_a (вообще говоря, радиус r_a является бесконечно малой величиной) в которой функция потенциала скорости не определена, а само потенциальное течение не существует.

В случае отрицательного объемного расхода потенциальное течение является стоком. В стоке жидкость равномерно со всех сторон втекает в начало координат.

Однородному поступательному течению соответствует взаимно обратное потенциальное течение, потенциалом скорости которого является функция тока исходного течения и наоборот, т.е. = uy;  = ux.

Это течение направлено вдоль оси Y, т.е. линии тока представляют собой семейство прямых, параллельных оси Y. Соответственно, эквипотенциали представляют собой семейство прямых, параллельных оси Х.

Аналогично, источнику соответствует взаимно обратное потенциальное течение, образованное из исходного заменой функции тока на потенциал скорости и обратно:

 = Q/2;  = Qlnr/2

Новое потенциальное течение называется циркуляционное безвихревое, которое также определено везде, за исключением особой окрестности радиуса r_a в начале координат.

Линии тока такого течения образуют семейство концентрических окружностей с общим центром в начале координат. Частицы жидкости движутся по окружностям вращаясь вокруг оси, проходящей через начало координат, и одновременно вращаясь вокруг собственных осей в противоположную сторону с одинаковыми угловыми скоростями, так что суммарное вращение жидких частиц отсутствует. В циркуляционном безвихревом течении величина Q уже не является объемным расходом жидкости через цилиндрическую поверхность единичной высоты, а имеет совершенно иной физический смысл.

Аналогично, стоку соответствует взаимно обратное потенциальное течение:

 = – Q/2  = – Qlnr/2

Это циркуляционное безвихревое движение отличается от предыдущего движением жидких частиц по окружностям в отрицательном направлении, т.е. по часовой стрелке.

Представляет интерес потенциальное течение, образованное взаимодействием источника со стоком одинакового расхода, причем источник и сток расположены на оси Х по разные стороны на одинаковом расстоянии dx от начала координат, так что 2Qdx = M = const при dx  0. В этом случае все линии тока выходящие из источника замкнутся на стоке. Можно показать, что линии тока нового потенциального течения, называемого диполем, образуют семейство неконцентрических окружностей, имеющих общую касательную - ось Х и общую точку касания - начало координат. Таким образом, функция тока есть:  = – My/2r²

В выражении для функции тока У - расстояние до данной точки по вертикальной оси, r - расстояние от начала координат. Соответственно семейство эквипотенциалей - это совокупность неконцентрических окружностей, имеющих общую касательную (ось Y) и общую точку касания [начало координат]:  = Mx/2r².

Представляет интерес потенциальное течение, образованное наложением однородного потенциального потока на диполь. В силу линейного свойства потенциала скорости и функции тока можно записать:

 = ux + Mx/2r² ;  = uy – My/2r²

Нулевая линия тока нового потенциального течения состоит из прямой, совпадающей с осью Х и окружности. Действительно, из условия  = 0 можно записать:

uy( 1 – M/2r₀² u )= 0

Т аким образом:

П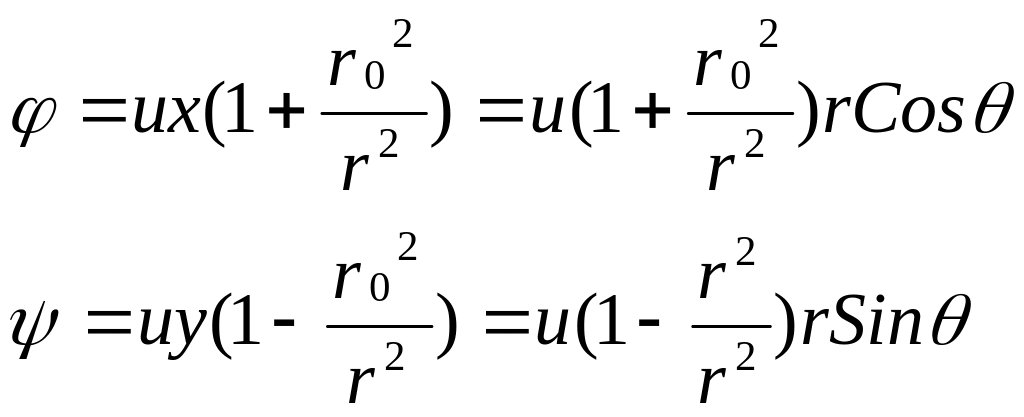 оэтому распределение линий тока вне окружности радиуса r₀ характеризует поперечное обтекание цилиндра радиусом r₀ идеальной жидкостью. При этом:

Скорости течения в полярной системе координат:

С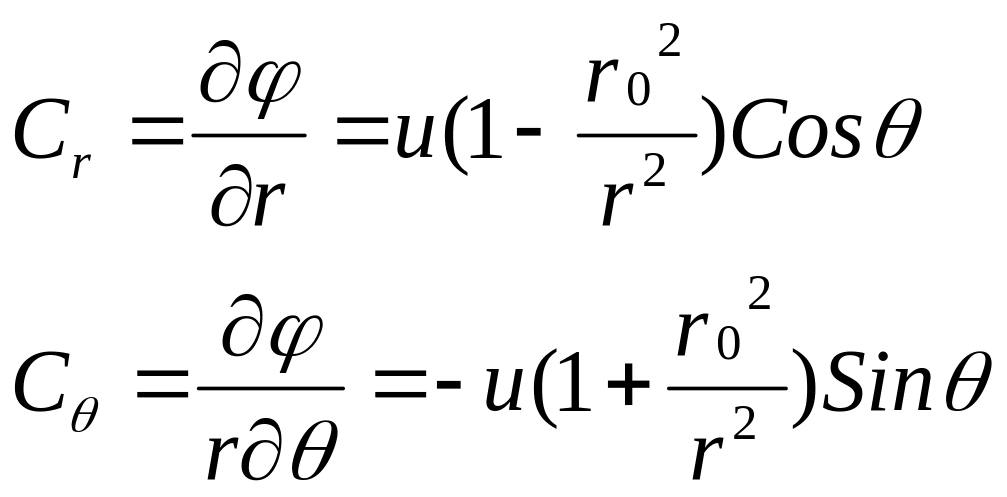 корости течения на поверхности цилиндра: Cr = 0; C_ = - 2uSin

С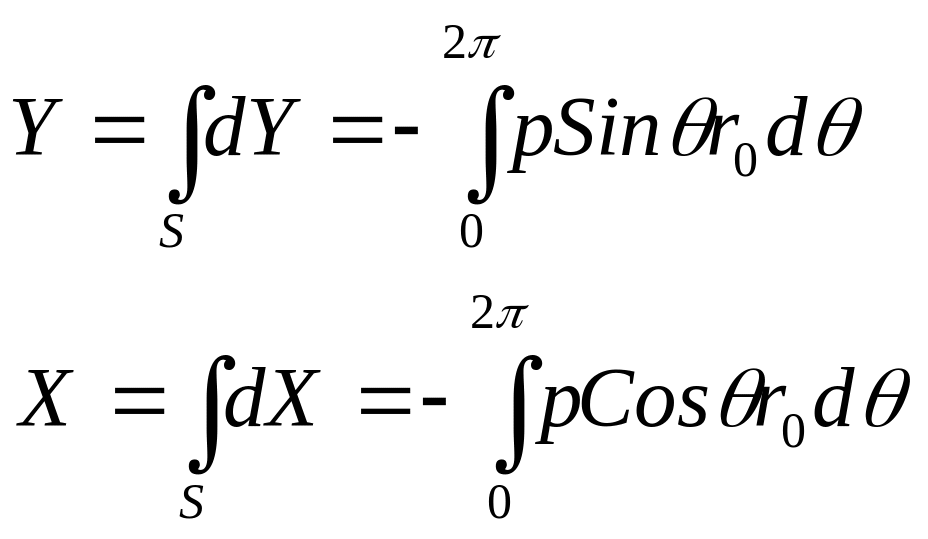 иловое взаимодействие потока с цилиндром определится как результат интегрирования по поверхности цилиндра единичной длины проекций силы давления на оси:

С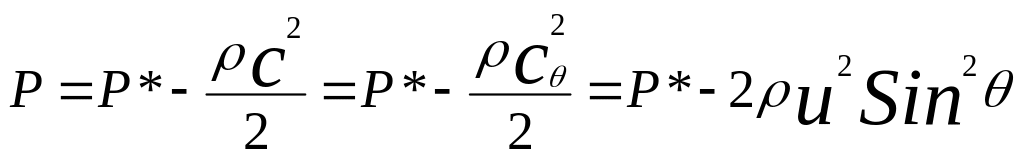 ила давления распределена по поверхности цилиндра согласно уравнению Бернулли для несжимаемой жидкости:

С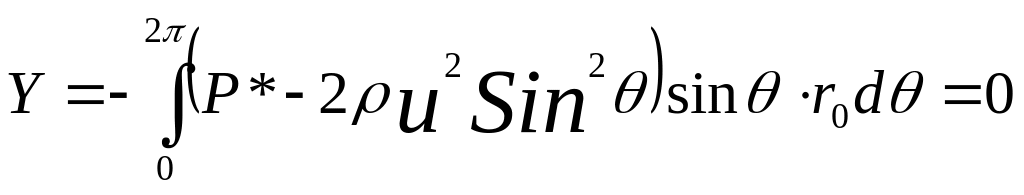 оответственно:

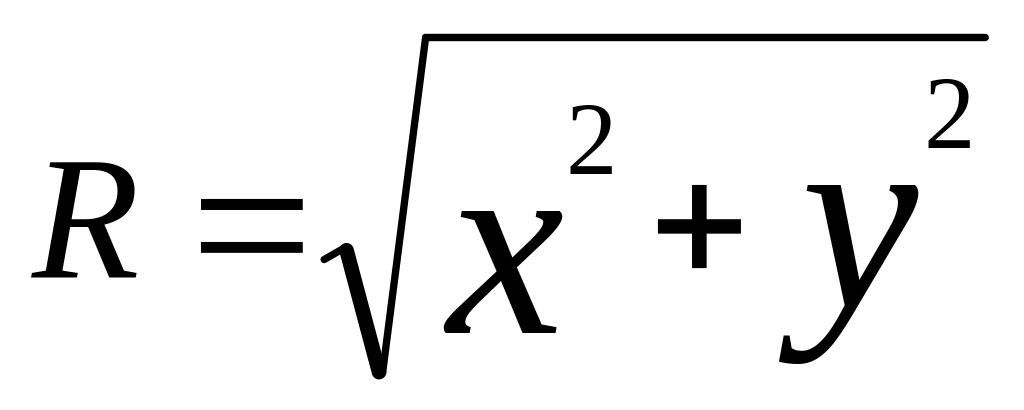
Результирующая сила действия потока на цилиндр также равна нулю.

Таким образом, на цилиндр, поперечно обтекаемый равномерным потоком идеальной несжимаемой жидкостью, не действует никакая сила. Можно показать методом конформных отображений, что полученный результат справедлив для тел любой формы. Это известно как парадокс Даламбера -Эйлера: При обтекании тел плоскопараллельным потенциальным потоком идеальной несжимаемой жидкости равнодействующая сил давления со стороны потока равна нулю.

В действительности на цилиндр всегда действует сила сопротивления. Происхождение парадокса связано с неучётом поля диссипативных сил трения. Наличие сил трения создаёт сопротивление как по причине появления проекции силы трения на направление потока, так и по причине нарушения симметричного распределения давления из -за явления отрыва вязкой жидкости.