
- •Рыбинская государственная авиационная технологическая академия Конспект Лекций по механике жидкости и газа
- •Оглавление
- •Введение Общая постановка задач в механике жидкости и газа.
- •Кинематические понятия и определения, используемые в прикладной гидрогазодинамике.
- •Классификация сил, действующих в жидкости при ее движении.
- •Глава 1. Одномерное энергоизолированное установившееся движение легкой идеальной жидкости.
- •1.1. Уравнение движения
- •Лёгкой идеальной жидкости в элементарной струйке тока.
- •1.2. Интегрирование уравнения движения.
- •1.3. Скорость звука
- •В элементарной трубке тока
- •1.4. Связь между формой струйки тока и величиной скорости сжимаемого газового потока, движущегося в условиях энергетической изолированности.
- •1.5. Вычисление массового расхода газа по параметрам торможения и приведенной скорости потока. Газодинамические функции расхода.
- •1.6. Газодинамический импульс. Газодинамические функции импульса.
- •Глава 2. Установившееся одномерное движение вязкого сжимаемого газа в канале переменного сечения при наличии энергообмена и массообмена с окружающей средой.
- •Глава 3. Одномерное установившееся движение вязкой жидкости в каналах постоянного сечения.
- •3.1. Описание турбулентных течений путем использования осредненных во времени величин
- •Степень турбулизации течения определяется интенсивностью турбулентности
- •3.2. Гипотеза турбулентности л. Прандтля. Понятие о длине пути перемешивания. Логарифмический профиль осредненной скорости.
- •3.3. Гидравлическое сопротивление круглых труб.
- •3.4. Гидравлические потери на местных сопротивлениях.
- •3.5. Взаимодействие потоков вязких жидкостей. Перемешивание газовых потоков. Потери смешения.
- •Глава 4. Движение вязкой жидкости вблизи твердой поверхности.
- •4.1. Пограничный слой.
- •Т аким образом:
- •4.2. Физическая толщина пограничного слоя. Интегральные толщины.
- •4.3. Интегральное соотношение для пограничного слоя
- •4.4. Методы расчёта пограничного слоя при наличии продольного градиента давления
- •Глава 5. Осреднение параметров газового потока.
- •Глава 6. Сверхзвуковое течение газа.
- •С пониженным давлением.
- •Глава 7. Основные уравнения в механике жидкости и газа.
- •7.1. Уравнение неразрывности.
- •7.2. Уравнение движения.
- •7.3. Дифференциальные уравнения движения.
- •При этом в силу равновесия элемента имеет место равенство моментов сил
- •7.4. Дифференциальные уравнения Навье-Стокса.
- •7.5. Уравнение энергии.
- •7.6. Дифференциальное уравнение энергии.
- •7.7. Дифференциальные уравнения Эйлера.
- •2 .Стационарное винтовое течение:
- •Глава 8. Потенциальное движение идеальной жидкости.
- •Глава 9. Вихревое течение идеальной несжимаемой жидкости.
- •Глава 10. Основы теории подобия
- •Глава 11. Связь энтропии газового потока с коэффициентом сохранения полного давления.
4.3. Интегральное соотношение для пограничного слоя
В пограничном слое силы трения соизмеримы с другими силами, действующими в жидкости, поэтому дифференциальные уравнения движения вязкой жидкости содержат вторые частные производные, что делает крайне затруднительным использование дифференциальных уравнений для решения конкретных задач о расчете пограничного слоя. Интегрирование параметров жидкости по толщине пограничного слоя позволяет избавиться от необходимости рассмотрения параметров жидкости и их производных в зависимости от поперечной координаты, что существенно упрощает математическое описание течения в пограничном слое до состояния, позволяющего произвести расчет несложными численными методами.
В самом деле, при обтекании твердой поверхности вязкой жидкостью (рис.11) по мере движения увеличивается расход жидкости через пограничный слой в связи с увеличением его толщины на величину, соответствующую расстоянию dx между сечениями 1-1 и 2-2.
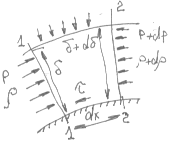
Рис.11. К выводу интегрального уравнения пограничного слоя.
П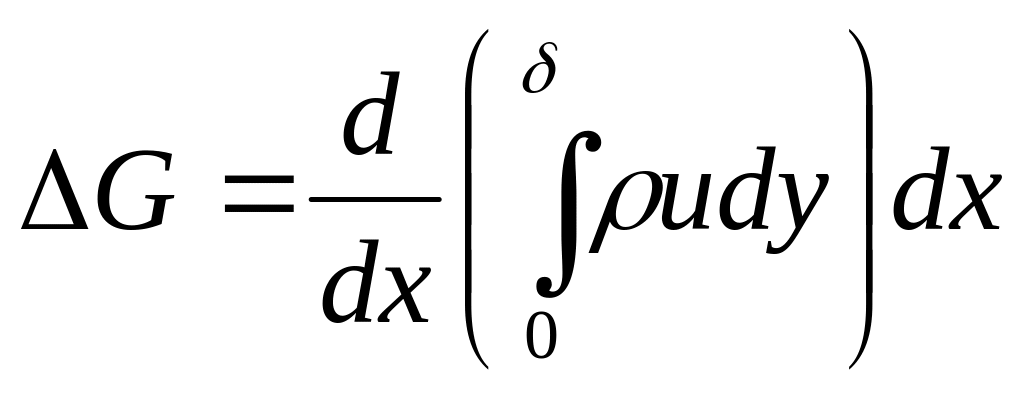
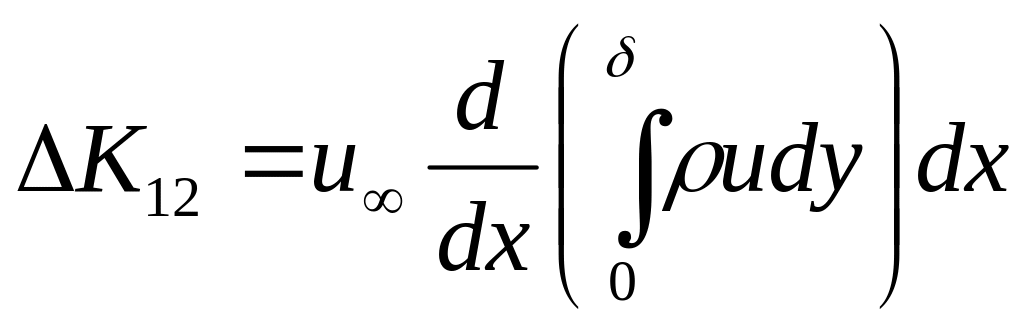 ри
этом количество движения, вносимое
жидкостью, втекающей в пограничный слой
через верхнюю грань 1-2, равно:
ри
этом количество движения, вносимое
жидкостью, втекающей в пограничный слой
через верхнюю грань 1-2, равно:
В![]() то же время количество движения в
пограничном слое между сечениями 1-1 и
2-2 уменьшается на величину:
то же время количество движения в
пограничном слое между сечениями 1-1 и
2-2 уменьшается на величину:
Очевидно, суммарное изменение количества движения в пограничном слое есть сумма K12 + K1122
С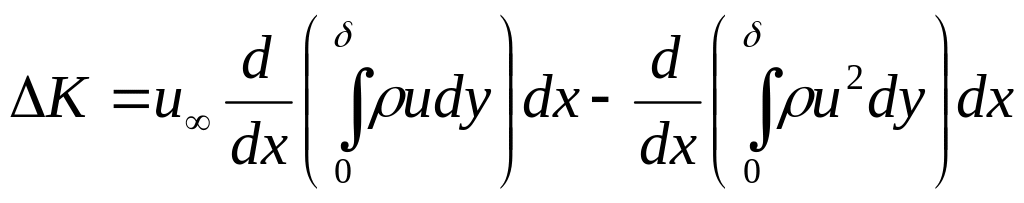 огласно
второму закону Ньютона это изменение
количества движения равно импульсу
всех внешних по отношению к элементу
жидкости 11 22 1 сил, а именно: сил давления
в сечениях 1-1 , 2-2, на границе 1-2 и сил
трения на твердой поверхности 2-1. Импульс
сил давления - есть
величина:
огласно
второму закону Ньютона это изменение
количества движения равно импульсу
всех внешних по отношению к элементу
жидкости 11 22 1 сил, а именно: сил давления
в сечениях 1-1 , 2-2, на границе 1-2 и сил
трения на твердой поверхности 2-1. Импульс
сил давления - есть
величина:
Iд = ( P + dP)( + d) – P – ( P + dP/2 ) d
Импульс сил трения – есть величина: Iт = dx.
С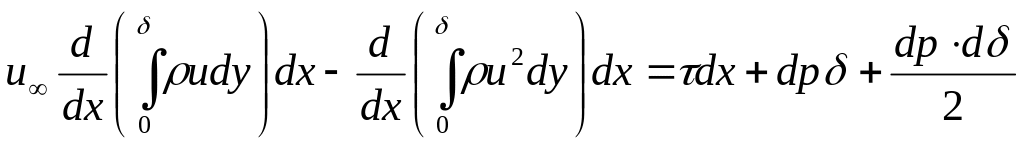 огласно
второму закону Ньютона:
огласно
второму закону Ньютона:
О
(119)![]() ставляя
в правой части уравнения члены одного
порядка. можно записать:
ставляя
в правой части уравнения члены одного
порядка. можно записать:
П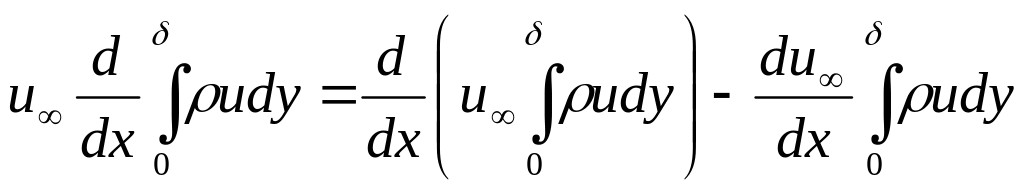 ервый
член в левой части по теореме о производной
произведения следует представить в
виде суммы:
ервый
член в левой части по теореме о производной
произведения следует представить в
виде суммы:
В![]() торой
член в правой части следует представить
как градиент скорости и перенести его
в левую часть.
торой
член в правой части следует представить
как градиент скорости и перенести его
в левую часть.
Т![]() огда:
огда:
![]()
![]()
![]()
Производную плотности в левой части уравнения следует записать через производную скорости.
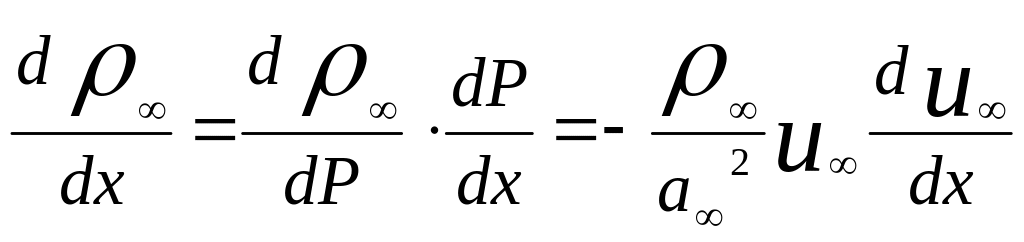
В![]() итоге:
итоге:
Далее вводятся обозначения: H = */** - формпараметр пограничного слоя;
Сf = / u2 - местный коэффициент трения.
У![]() равнение
для изменения количества движения в
пограничном слое записывается в виде:
равнение
для изменения количества движения в
пограничном слое записывается в виде:
(120)
Уравнение (120) является основным интегральным соотношением теории пограничного слоя и широко используется в расчетах. Уравнение (120) пригодно для расчета как ламинарного, так и турбулентного пограничного слоя, поскольку при его выводе не делалось никаких предположений о характере течения в пограничном слое, а также о природе и величине напряжения трения на стенке.
Поскольку уравнение (120) является дифференциальным уравнением первого порядка в полных производных, то возможно его численное интегрирование или даже решение в квадратурах (представление как комбинации аналитических функций), если соответствующие коэффициенты постоянны. При этом необходимо задать профиль скорости u = f (y) и закон изменения трения по продольной координате Cf = f (x). По заданному профилю скорости вычисляется формпараметр Н, в результате чего, имея зависимость трения от продольной координаты можно численно интегрировать уравнение (120) и получить закон изменения толщины потери импульса от продольной координаты.
При этом задание профиля скорости не противоречит логике, как это может показаться. Действительно, если известен профиль скорости, то сразу же можно вычислить толщину потери импульса, не прибегая к дальнейшим вычислениям, а если задан коэффициент трения, то сразу же можно вычислить напряжение трения. Дело однако в том, что и профиль скорости и напряжения трения, вообще говоря, неизвестны. Поэтому их задание на основе каких–либо соображений является более или менее правдоподобной гипотезой. Уравнение (120) является математической формулировкой известного физического закона, что и позволяет обоснованно определить толщину потери импульса. При этом произвольное задание профиля не влияет на конечный результат вычислений потому что операция интегрирования заданного профиля по толщине пограничного слоя сама по себе нивелирует допускаемую погрешность. Кроме того, в результате вычисляется формпараметр Н, в числителе и знаменателе которого представлены сходные интегралы, что в результате деления одной вычисленной с погрешностью величины на другую с аналогичной погрешностью величину тем более умаляет погрешность, возникающую при задании профиля скорости, отличающегося от действительного.
Что касается задаваемого с определенной погрешностью коэффициента трения, то его величина может быть уточнена после вычисления толщины потери импульса.
Расчет безградиентного пограничного слоя.
Пограничный слой, развивающийся на плоской пластине при ее продольном обтекании равномерным потоком, является безградиентным. Это наиболее простой случай течения при условии движения несжимаемой жидкости. При этом для ламинарного режима течения возможно получить аналитическое решение, не прибегая к использованию опытных данных или задаваемых величин.
Известно, что в ламинарном пограничном слое профиль скорости описывается параболитической зависимостью: u = a + b +cy2.
Здесь а, в, с, - постоянные, подлежащие определению из граничных условий.
В данном случае граничные условия следующие:
1![]() .
на твердой
стенке скорость равна нулю т.е.
.
на твердой
стенке скорость равна нулю т.е.
2. на границе пограничного слоя местная скорость совпадает со скоростью набегающего потока (с погрешностью не более 1 %) т.е.
3![]()
![]() .
на границе
пограничного слоя ввиду отсутствия
поперечного градиента скорости
отсутствуют силы трения, т.е.
.
на границе
пограничного слоя ввиду отсутствия
поперечного градиента скорости
отсутствуют силы трения, т.е.
В соответствии с граничным условием профиль скорости имеет вид:
u = u (2y / - y2 / 2)
При этом местное напряжение трения определяется по формуле Ньютона:
= (du / dy)y = 0 = 2 u /
И нтегральное
уравнение для безградиентного
пограничного слоя согласно (119) записывается
в виде:
нтегральное
уравнение для безградиентного
пограничного слоя согласно (119) записывается
в виде:
О ба
интеграла в левой части уравнения
вычисляются по известному профилю
скорости.
ба
интеграла в левой части уравнения
вычисляются по известному профилю
скорости.
В результате: (2 u2 / 15) d/ dx = 2 u / :
После разделения переменных: d/ u) dx
Интеграл последнего уравнения: 2 / 2 = x / u + const:
П остоянная
интегрирования определится из граничного
условия на передней кромке:
остоянная
интегрирования определится из граничного
условия на передней кромке:
= 0
x = 0
Т
(121)![]()
В уравнении (121) v=μ/ρ
При этом напряжение трения на стенке:
(122)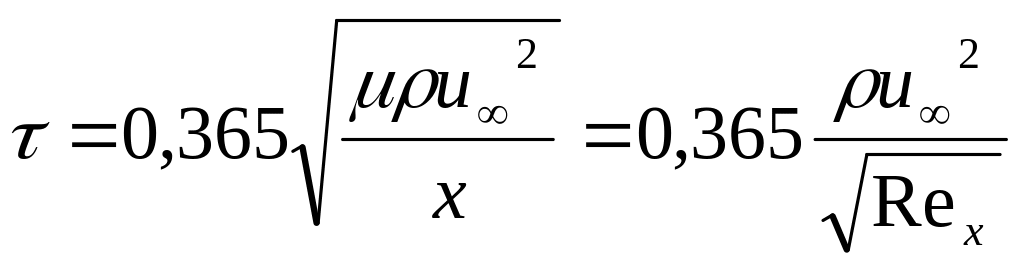
Таким образом, в ламинарном слое толщина пограничного слоя возрастает пропорционально корню расстояния от передней кромки, а местное напряжение трения убывает обратно пропорционально корню расстояния от передней кромки.
Следует отметить, что применение формулы (122) в окрестности передней кромки (x 0) дает физически неправдоподобный результат ( ). На самом деле, напряжение трения вблизи передней кромки конечно, а полученный результат связан с интенсивным поперечным течением вблизи передней кромки (где продольная и поперечная скорости соизмеримы, что противоречит основной гипотезе о пограничном слое). Поэтому, вычислять местное напряжение трения по формуле (122) можно только за пределами окрестности передней кромки (величина этой окрестности определяется на основе каких –либо дополнительных соображений или по опытным данным ).
О![]() днако
особенность течения в районе передней
кромки не влияет на правильность
определения полной силы трения,
действующей на пластину из–за того,
что указанная особенность ограничена
(вообще говоря, формула
(122) неверна только при x
0). Действительно, сила трения, действующая
на одну сторону пластины шириной b и
длинной L определится как результат
интегрирования:
днако
особенность течения в районе передней
кромки не влияет на правильность
определения полной силы трения,
действующей на пластину из–за того,
что указанная особенность ограничена
(вообще говоря, формула
(122) неверна только при x
0). Действительно, сила трения, действующая
на одну сторону пластины шириной b и
длинной L определится как результат
интегрирования:
В случае турбулентного режима течения в пограничном слое (во всем пограничном слое начиная с передней кромки)нельзя аналитическим образом определить характеристики пограничного слоя.
Д

 ело
в том, что в соответствии с граничными
условиями для вязкой жидкости на твердой
стенке u
0
ело
в том, что в соответствии с граничными
условиями для вязкой жидкости на твердой
стенке u
0
y0
 любое
движение, в том числе и турбулентное,
запрещено вблизи твердой поверхности.
поэтому в любом, сколь угодно
турбулизированном течении в пограничном
слое, существует так называемый ламинарный
подслой, физический характер движения
в котором является ламинарным. В этой
связи следует понимать, что не может
существовать единой аналитической
зависимости для профиля скорости по
всей толщине пограничного слоя в силу
разных физических механизмов поперечного
переноса импульса в турбулентной и
ламинарной части слоя. Между тем, местное
напряжение трения определяется по
закону Ньютона дифференцированием
профиля скорости. При использовании
опытной аппроксимации профиля скорости
возникает недопустимая погрешность
для величины местного напряжения трения
по той же причине. Поэтому для вычисления
характеристик турбулентного пограничного
слоя с помощью интегрального соотношения
(119) необходимо воспользоваться опытными
данными как для профиля скорости, так
и для напряжения трения.
любое
движение, в том числе и турбулентное,
запрещено вблизи твердой поверхности.
поэтому в любом, сколь угодно
турбулизированном течении в пограничном
слое, существует так называемый ламинарный
подслой, физический характер движения
в котором является ламинарным. В этой
связи следует понимать, что не может
существовать единой аналитической
зависимости для профиля скорости по
всей толщине пограничного слоя в силу
разных физических механизмов поперечного
переноса импульса в турбулентной и
ламинарной части слоя. Между тем, местное
напряжение трения определяется по
закону Ньютона дифференцированием
профиля скорости. При использовании
опытной аппроксимации профиля скорости
возникает недопустимая погрешность
для величины местного напряжения трения
по той же причине. Поэтому для вычисления
характеристик турбулентного пограничного
слоя с помощью интегрального соотношения
(119) необходимо воспользоваться опытными
данными как для профиля скорости, так
и для напряжения трения.
Экспериментально установлено, что в турбулентном пограничном слое распределение скоростей приближенно может быть представлено степенной зависимостью
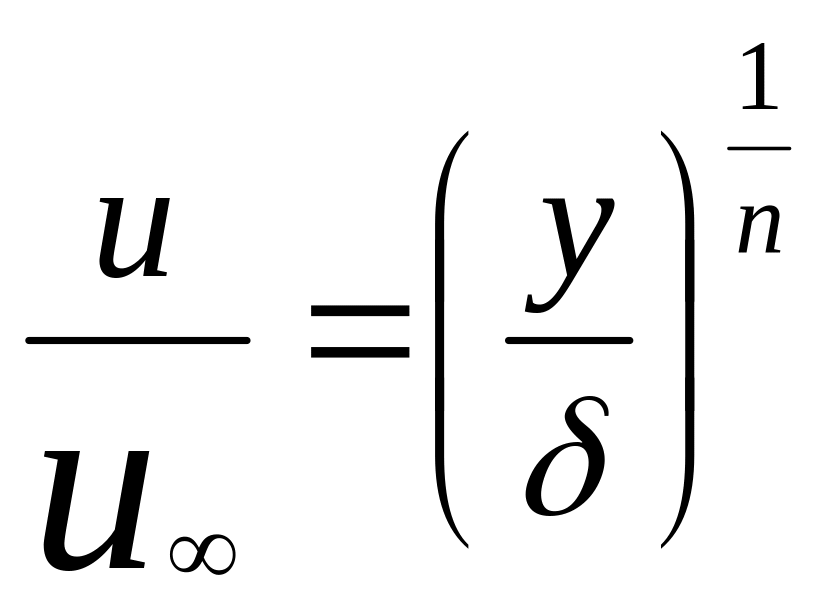
Показатель степени n в зависимости от числа Рейнольдса меняется в пределах от 6 до 10. В большинстве практически важных случаев можно принять n = 7 (закон одной седьмой).
М
,
где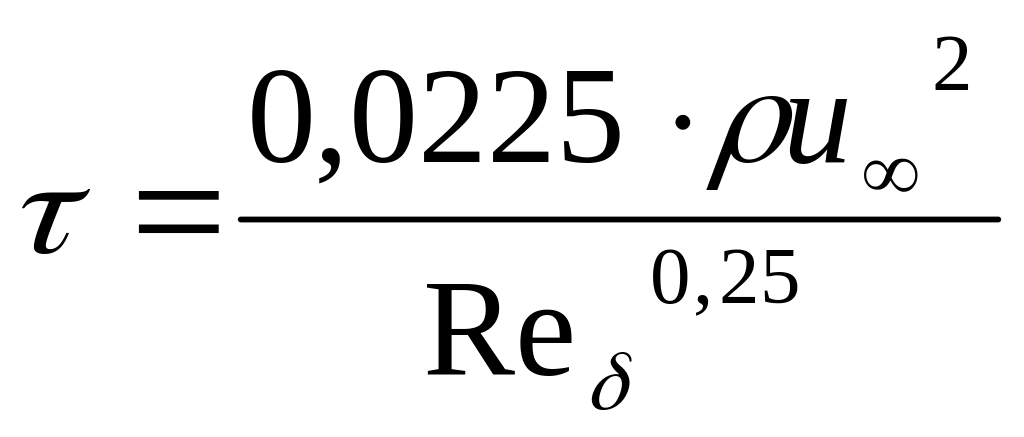
![]()
С учётом опытных данных для профиля скорости и местного напряжения трения интегральное уравнение для пограничного слоя запишется следующим образом:
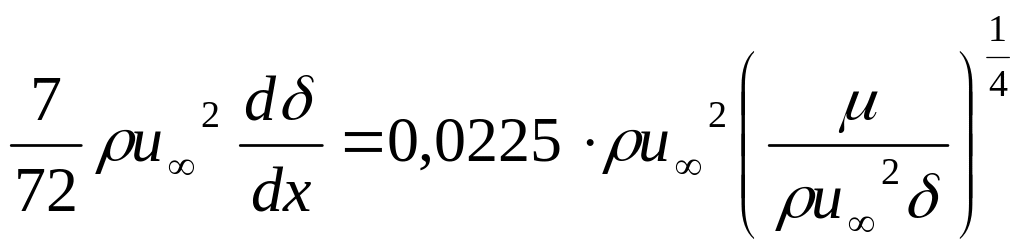
П![]() осле
разделения переменных
осле
разделения переменных
И
(123)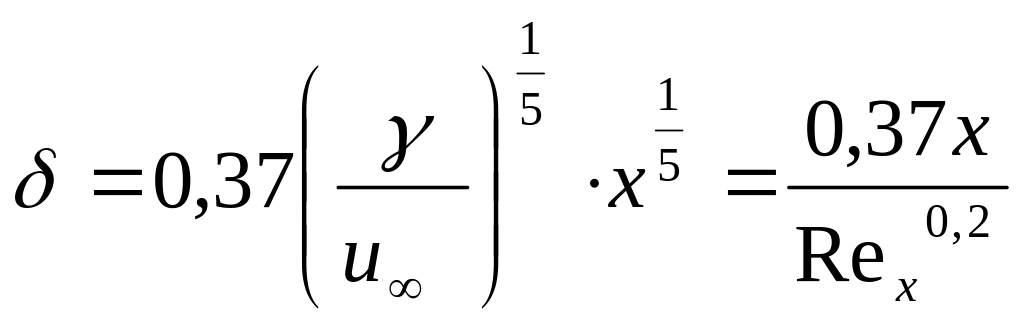
П![]() о
известной толщине определится местное
напряжение трения из формулы
о
известной толщине определится местное
напряжение трения из формулы
С
(124)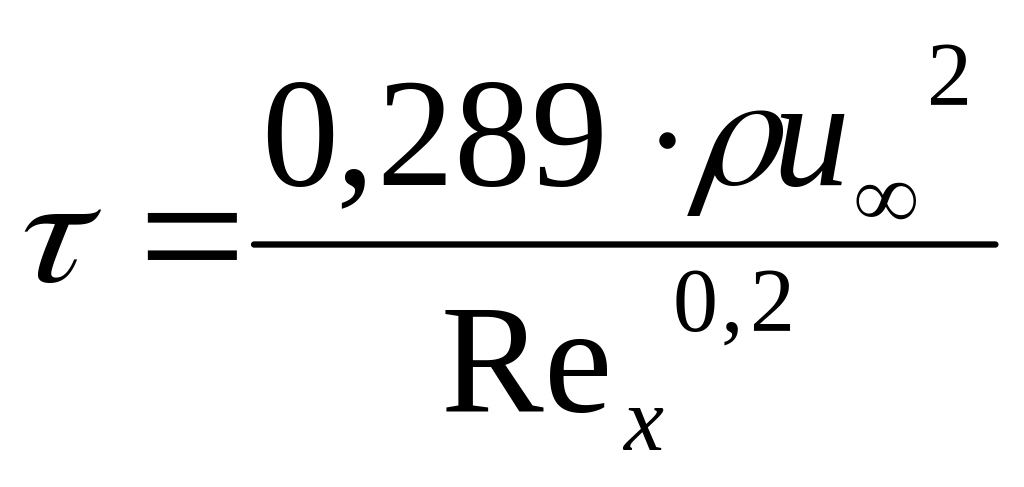 ила
трения, действующая на одну сторону
пластины определится в результате
интегрирования:
ила
трения, действующая на одну сторону
пластины определится в результате
интегрирования:
И
,
где![]()
![]() з
полученных результатов видно, что
турбулентный пограничный слой при
прочих равных условиях толще ламинарного,
нарастает более интенсивно, чем ламинарный
местное напряжение трения в турбулентном
пограничном слое больше, чем в ламинарном,
а по длине пластины оно уменьшается
медленнее. Вместе с тем в обоих случаях
толщины пограничного слоя, местные
напряжения трения и коэффициенты трения
уменьшаются с увеличением числа
Рейнольдса.
з
полученных результатов видно, что
турбулентный пограничный слой при
прочих равных условиях толще ламинарного,
нарастает более интенсивно, чем ламинарный
местное напряжение трения в турбулентном
пограничном слое больше, чем в ламинарном,
а по длине пластины оно уменьшается
медленнее. Вместе с тем в обоих случаях
толщины пограничного слоя, местные
напряжения трения и коэффициенты трения
уменьшаются с увеличением числа
Рейнольдса.
Течение сжимаемого газа в пограничном слое физически сложнее движения в несжимаемом газе. Дело в том, что в сжимаемом газе плотность и вязкость являются переменными по толщине слоя величинами в связи с эффектом разогрева газа при его подтормаживании в пограничном слое. При этом уменьшение плотности газа вблизи поверхности обтекаемого тела приводит к уменьшению числа Рейнольда. Вязкость газа увеличивается с увеличением температуры, что также имеет следствием уменьшение числа Рейнольда. Поэтому при прочих равных условиях сжимаемый пограничный слой толще несжимаемого, а местный коэффициент трения и местное напряжение трения в нём меньше.
Р![]() асчёт
сжимаемого пограничного слоя следует
проводить по интегральному уравнению
для пограничного слоя, однако, можно
воспользоваться результатами расчёта
несжимаемого пограничного слоя, внеся
в них соответствующие поправки. Так, в
частности, плотность газа обратно
пропорциональна температуре и связана
с числом Маха известным соотношением:
асчёт
сжимаемого пограничного слоя следует
проводить по интегральному уравнению
для пограничного слоя, однако, можно
воспользоваться результатами расчёта
несжимаемого пограничного слоя, внеся
в них соответствующие поправки. Так, в
частности, плотность газа обратно
пропорциональна температуре и связана
с числом Маха известным соотношением:
Известна и связь вязкости с температурой, а значит и с числом Маха:
В![]()
![]() последней формуле
-
опытный
коэффициент. Поскольку температура
поперёк пограничного слоя переменна,
то необходимо соответствующие параметры
определять по некоей средней температуре
между температурой торможения и
статической температурой невозмущённого
потока.
последней формуле
-
опытный
коэффициент. Поскольку температура
поперёк пограничного слоя переменна,
то необходимо соответствующие параметры
определять по некоей средней температуре
между температурой торможения и
статической температурой невозмущённого
потока.
В![]() последней формуле
- постоянный коэффициент, лежащий в
пределах 0 <
<1, величена которого может быть
подобрана из условия наилучшего
согласования с опытными данными (при
= 0, Тср
= Т*, а при
= 1, Тср
= Т)
Поскольку вязкость и плотность в
одинаковой степени входят в число
Рейнольдса, то справедлива зависимость:
последней формуле
- постоянный коэффициент, лежащий в
пределах 0 <
<1, величена которого может быть
подобрана из условия наилучшего
согласования с опытными данными (при
= 0, Тср
= Т*, а при
= 1, Тср
= Т)
Поскольку вязкость и плотность в
одинаковой степени входят в число
Рейнольдса, то справедлива зависимость:
П![]() оказатель
степени m зависит от режима течения,
при турбулентном режиме течения m = 0,2.
Поскольку известна зависимость плотности
и вязкости газа от температуры, то
последняя формула может быть записана
в виде:
оказатель
степени m зависит от режима течения,
при турбулентном режиме течения m = 0,2.
Поскольку известна зависимость плотности
и вязкости газа от температуры, то
последняя формула может быть записана
в виде:
С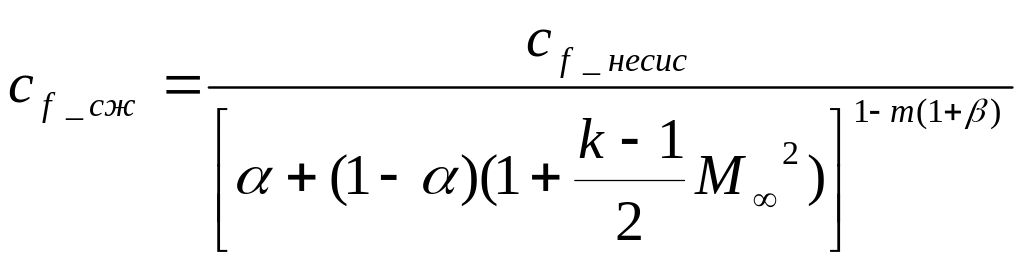 оответственно,
выражение для местного коэффициента
трения имеет вид:
оответственно,
выражение для местного коэффициента
трения имеет вид:
Наилучшее совпадение с опытными данными наблюдается при = 2\3.
