7.3. Дифференциальные уравнения движения.

Дифференциальные уравнения движения в напряжениях получаются в результате применения второго закона Ньютона к элементарному жидкому объёму dV = dx dy dz с постоянной массой dm = dV. Уравнение второго закона Ньютона в проекции на ось Х для рассматриваемой жидкой частицы [рис.21] имеет вид:

d(u  dV) / dt =  dV du / dt = dR_x

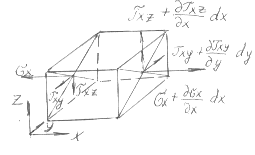
Рис. 21. Составляющие напряжений на гранях перпендикулярных оси Х.

Величина dm = dV вынесена за знак дифференциала как постоянная масса рассматриваемого непроницаемого элемента.

Сила dR_x складывается из проекции массовой силы, действующей на выделенный элемент жидкости, и проекций сил, обусловленных нормальными и касательными напряжениями.

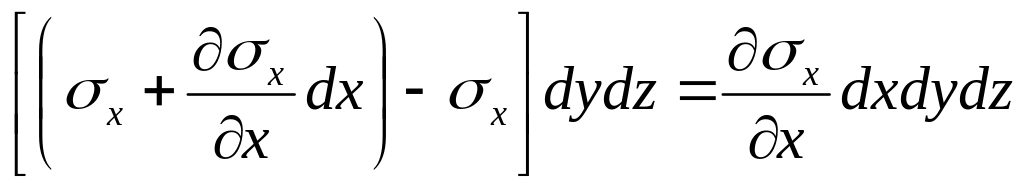Проекция массовой силы на ось Х составит величину X  dV, где Х - напряжение массовой силы в направлении оси Х. Нормальные напряжения на гранях, перпендикулярных оси Х, [рис.21] создают силу в направлении оси Х.

Тангенциальные [касательные] напряжения, действующие на гранях, перпендикулярных оси Y, создают силу в направлении оси Х [рис.22]

Рис.22 Составляющие напряжений на гранях, перпендикулярных оси Y.

Тангенциальные напряжения, действующие на гранях, перпендикулярных оси z, создают силу в направлении оси x (Рис.23.)

Рис.23.Составляющие напряжений

на гранях, перпендикулярных оси Z.

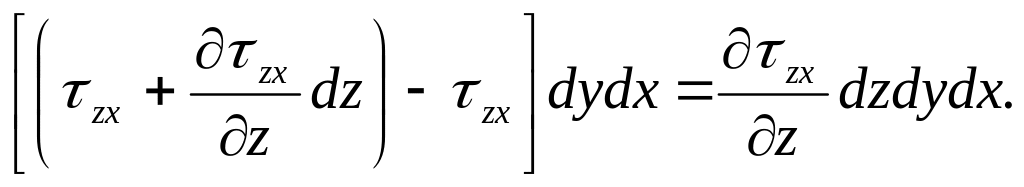
При этом в силу равновесия элемента имеет место равенство моментов сил

( _xy dy dz )dx = ( _yx dx dz ) dy

Откуда следует условие парности касательных напряжений: _xy = _yx.

А налогично: _xz = _zx. В итоге:

П оэтому второй закон Ньютона в проекции на ось Х запишется в виде:

Аналогично составляются уравнения движения в проекции на оси Y и Z. Таким образом, получаются дифференциальные уравнения движения в напряжениях:

П

(145)

ричём, поскольку скорость зависит от координат и времени, то полные производные в левой части уравнений представляют сумму:

Уравнения движения в напряжениях содержат 6 компонент напряжений (3 нормальных и 3 касательных напряжения), которые следует выразить через компоненты скорости имея в виду замкнуть систему уравнений сохранения и таким образом решить основную задачу газовой динамики.

7.4. Дифференциальные уравнения Навье-Стокса.

Дифференциальные уравнения неустановившегося пространственного движения сжимаемой вязкой жидкости ( уравнения Навье-Стокса ) получаются из дифференциальных уравнений движения в напряжениях путем введения связи между напряжениями и скоростями относительных деформаций элемента жидкости, выраженных через скорости поступательного движения.

Согласно закону вязкого трения при однонаправленной деформации сдвига в жидкости:

Пусть скорость С направлена по оси Х при однонаправленной деформации сдвига, тогда:  =  du / dy = d (dx / dt) / dy = ( / dt )dx/dy= d/dt, где d = dx/dy

- угловая деформация элемента жидкости в плоскости ХОY.

В случае пространственного движения вязкой жидкости угловые деформации элемента происходят одновременно в трёх взаимно перпендикулярных плоскостях. Например, в плоскости ХОY [рис.24] справедливо условие:

d_xy = d_x + d_y

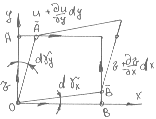
Рис.24. Связь между скоростями и деформациями жидкого элемента в плоскости ХОY.

У гловая деформация d_y обусловлена тем обстоятельством, что продольная составляющая скорости [по оси Х] точки А больше соответствующей скорости точки О. Поэтому:

А налогично для касательных напряжений в гранях, перпендикулярных плоскости ХОУ:

Причём опять-таки справедливо условие парности касательных напряжений:

_xz = _zx ; _yz = _zy

В случае отсутствия касательных напряжений (т.е. при отсутствии вязкости) нормальные напряжения возникают только под действием давления, так что:

_x = _y = _z = – P

Однако при наличии вязкости нормальные напряжения обусловлены не только давлением, но и действием касательных напряжений, уменьшающих или увеличивающих величину нормального давления в зависимости от ориентации площадки, так что можно записать:

_x = – P +_x' ; _y = – P +_y' ; _z = – P +_z'

Дополнительные нормальные напряжения _x', _y', _z' обусловлены линейными и объёмными деформациями элемента жидкости. В несжимаемой жидкости в связи с отсутствием объёмных деформаций дополнительные нормальные напряжения обусловлены только соответствующими касательными напряжениями и могут быть выражены в соответствии с законом вязкого трения через скорости продольных деформаций вдоль соответствующих осей с тем же коэффициентом пропорциональности. При этом следует иметь в виду, что нормальные напряжения, действующие в каком - либо направлении, всегда вызывают деформации на четырёх гранях [плоскостях], перпендикулярных вектору нормальных напряжений. В то время как при однонаправленной деформации сдвига несжимаемой жидкости [для какой и получен опытным путём закон вязкого трения] касательные напряжения действуют только на двух противоположных гранях. Поэтому с точки зрения закона вязкого трения в несжимаемой жидкости дополнительные нормальные напряжения должны быть связаны с продольными деформациями жидких элементов следующим образом:

где

- продольная деформация элемента жидкости.

Д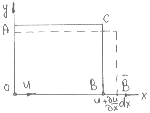 ействительно, линейная деформация жидкого элемента в направлении оси Х (рис.25) обусловлена тем обстоятельством, что продольная скорость (вдоль оси Х ) грани ОА меньше продольной скорости грани ВС.

Рис. 25. Связь между скоростями и деформациями жидкого элемента в плоскости XOY

П ри этом

А налогично:

В случае сжимаемой жидкости величина относительной объемной деформации выглядит:

С корость объемной деформации составит величину:

П ри движении несжимаемой жидкости величина относительной объемной деформации в силу определения в любой момент времени нулевая, соответственно и скорость объемной деформации также нулевая, т.е.

При этом скорость линейной деформации в каком - либо направлении, вообще говоря, не нулевая, однако алгебраическая сумма скоростей линейных деформаций по любым трём взаимно перпендикулярным направлениям равна нулю.

П ри движении сжимаемой жидкости величина и соответственно скорость продольной деформации отличается от соответствующих величин для несжимаемой жидкости при прочих равных условиях. При объемной деформации растяжения, если скорость увеличения объема под действием внутренних сил будет такой же, как и скорость увеличения объема за счет внешних сил(напряжений), то деформации не возникнет вообще, а значит не возникнет дополнительных нормальных напряжений. При этом следует учесть, что положительные нормальные напряжения увеличивают объем. Разумно предположить, что увеличение объема сжимаемой жидкости происходит равномерно во всех направлениях, чему соответствует уменьшение скорости деформации вдоль каждой оси на величину: de/3dt = (div c)/3

П оэтому для дополнительных нормальных напряжений справедливы соотношения:

В результате подстановки уравнений связи межу напряжениями и деформациями в дифференциальные уравнения движения в напряжениях получаются дифференциальные уравнения Навье - Стокса.

В

(147)

векторной форме уравнения Навье - Стокса имеют вид:

В уравнении (147)  = / - кинематическая вязкость жидкости, J - вектор массовых сил,

- оператор Лапласа.

У равнения Навье - Стокса лежат в основе современной механики сжимаемой вязкой жидкости. Интегрирование этих уравнений для общего случая движения жидкости встречает непреодолимые математические трудности. Поэтому большинство гидродинамических задач решается приближенно при введении различного рода упрощений. В частности при движении несжимаемой жидкости = const; div c = 0, а уравнения Навье - Стокса имеют вид:

При движении легкой несжимаемой жидкости (газа) пренебрегают массовыми силами (силами тяжести ). В этом случае:

При движении очень вязкой жидкости пренебрегают инерционными членами dc / dt.

В случае установившегося одномерного течения идеальной жидкости при отсутствии массовых сил уравнения Навье - Стокса принимают простейший вид:

c dc / dx = – dP /  dx