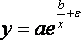- •1. Эконометрическая модель и проблемы эконометрического моделирования
- •1.1. Общие понятия
- •1.2. Экономическая модель
- •1.3. Эконометрическая модель
- •1.4. Элементы эконометрической модели и их свойства
- •1.5. Задачи эконометрики
- •1.6. Эконометрика и её место в ряду математических и экономических дисциплин
- •1.7. Резюме по теме.
- •1.8. Вопросы для повторения
- •2. Элементы теории вероятностей и математической статистики
- •2.1. Дискретные, непрерывные случайные величины
- •2.2. Зависимые случайные величины
- •2.3. Понятия генеральной совокупности и выборки (выборочной совокупности)
- •2.4. Оценки параметров генеральной совокупности. Несмещённость и состоятельность оценок
- •2.5. Резюме по теме
- •2.6. Вопросы для повторения
- •3. Модели и методы регрессионного анализа
- •3.1. Основные понятия регрессионного анализа
- •3.2. Линейная парная регрессия
- •3.2.1. Определения
- •3.2.2. Принцип, метод наименьших квадратов
- •3.2.3. Свойства оценок параметров парной линейной регрессии
- •3.2.4. Анализ статистической значимости коэффициентов линейной регрессии
- •3.3. Нелинейная регрессия
- •3.4. Характеристики парной регрессии
- •3.5. Множественная регрессия
- •3.6. Гомо- и гетероскедастичность остатков
- •Методы определения гетероскедастичности
- •Тест ранговой корреляции Спирмена
- •3.7. Резюме по теме.
- •3.8. Вопросы для повторения
- •4. Анализ временных рядов
- •4.1. Общие понятия
- •4.2. Понятие временного ряда
- •4.3. Основные понятия и модели анализа временных рядов
- •4.4. Трендовые модели генерации значений временного ряда.
- •4.5. Фильтрация и сглаживание временного ряда
- •4.5.1. Медианная фильтрация (сглаживание)
- •Проверка гипотезы о наличии тренда во временном ряде
- •4.6. Методы сглаживания временного ряда
- •4.6.1. Общие понятия
- •4.6.2. Аналитические методы
- •4.6.3. Метод скользящего среднего
- •4.6.4. Метод экспоненциально взвешенного скользящего среднего (метод Брауна)
- •4.7. Стационарные временные ряды
- •4.7.1. Основные понятия
- •4.7.2. Корреляционная функция
- •4.7.3. Использование автокорреляции для выявления структуры временного ряда
- •4.8. Модели авторегрессии стационарных временных рядов и их идентификация
- •4.8.1. Основные понятия
- •4.8.2. Модель авторегрессии 1-го порядка
- •4.8.3. Модель авторегрессии второго порядка
- •4.8.4. Оценивание параметров моделей авторегрессии. Метод инструментальных переменных.
- •4.9. Моделирование сезонных и циклических колебаний
- •4.9.1. Расчет сезонной компоненты и построение модели временного ряда
- •4.9.2. Использование сезонных фиктивных компонент при моделировании сезонных колебаний
- •4.10. Специфика изучения взаимосвязей по временным рядам. Исключение сезонных колебаний. Исключение тенденции.
- •4.10.1. Метод отклонений от тренда
- •4.10.2. Метод последовательных разностей
- •4.11. Резюме по теме.
- •4.12. Вопросы для повторения
- •5. Системы одновременных уравнений
- •5.1. Модель спроса и предложения
- •5.2. Структурная и приведённая форма системы
- •5.3. Идентифицируемость систем одновременных уравнений
- •5.4. Резюме по теме.
- •5.5. Вопросы для повторения
- •Задачник
- •Примеры решения типовых задач
- •Задачи для самостоятельного решения
- •Варианты задач
- •Нелинейные модели регрессии и их линеаризация
- •Решение типовых задач
- •Задачи для самостоятельного решения.
- •Варианты задач
- •Решение типовых задач.
- •Постановка задачи
- •Варианты для самостоятельного решения.
3.2.4. Анализ статистической значимости коэффициентов линейной регрессии
Величины yi, соответствующие
данным xi, при
некоторых теоретических значениях 0 и 1,
являются случайными. Следовательно,
случайными являются и рассчитанные по
ним значения коэффициентов b0 и b1. Их
математические ожидания при выполнении
предпосылок об отклонениях i равны,
соответственно, 0 и 1.
При этом оценки тем надежнее, чем меньше
их разброс вокруг 0 и 1,
то есть дисперсия. По определению
дисперсии ![]()
![]() Надежность
получаемых оценок а и b зависит,
очевидно, от дисперсии случайных
отклонений i,
но поскольку по данным выборки эти
отклонения (и, соответственно, их
дисперсия) оценены быть не могут, они
заменяются при анализе надежности
оценок коэффициентов регрессии на
отклонения переменной у от
оцененной линии регрессии
Надежность
получаемых оценок а и b зависит,
очевидно, от дисперсии случайных
отклонений i,
но поскольку по данным выборки эти
отклонения (и, соответственно, их
дисперсия) оценены быть не могут, они
заменяются при анализе надежности
оценок коэффициентов регрессии на
отклонения переменной у от
оцененной линии регрессии ![]() .
.
Можно доказать (доказательство опускаем), что
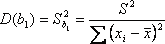
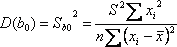 ;
;
где ![]() – мера
разброса
– мера
разброса
зависимой переменной вокруг линии регрессии (необъясненная дисперсия). Sb0 и Sb1 - стандартные отклонения случайных величин b0 и b1. Полученный результат можно проинтерпретировать следующим образом.
Коэффициент b1 есть мера наклона линии регрессии. Очевидно, чем больше разброс значений у вокруг линии регрессии, тем больше (в среднем) ошибка в определении наклона линии регрессии. Если такого разброса нет совсем (еi = 0 и, следовательно, 2=0), то прямая определяется однозначно и ошибки в расчете коэффициентов b0 и b1 отсутствуют (а отсюда и значение S1, "замещающее" 2, равно нулю).
В
знаменателе величины D(b1) стоит
сумма квадратов отклонений х, от
среднего значения ![]() . Эта
сумма велика в том случае, если регрессия
оценена на достаточно широком диапазоне
значений переменной х, и в этом случае,
при данном уровне разброса S2,
очевидно, ошибка в оценке величины
наклона прямой будет меньше, чем при
малом диапазоне изменения переменной
х. Если х1,
и х2,
лежат рядом, то даже небольшое изменение
одного из уiсущественно
меняет наклон прямой (если х1 и
х2 далеки
друг от друга - ситуация обратная).
. Эта
сумма велика в том случае, если регрессия
оценена на достаточно широком диапазоне
значений переменной х, и в этом случае,
при данном уровне разброса S2,
очевидно, ошибка в оценке величины
наклона прямой будет меньше, чем при
малом диапазоне изменения переменной
х. Если х1,
и х2,
лежат рядом, то даже небольшое изменение
одного из уiсущественно
меняет наклон прямой (если х1 и
х2 далеки
друг от друга - ситуация обратная).
Кроме
того, чем больше (при прочих равных)
число наблюдений n,
тем больше ![]() и,
тем самым, меньше стандартная ошибка
оценки. Дисперсия свободного члена
уравнения регрессии равна
и,
тем самым, меньше стандартная ошибка
оценки. Дисперсия свободного члена
уравнения регрессии равна
![]() .
.
- она пропорциональна D(b) и, тем самым, соответствует уже сделанным пояснениям о влиянии разброса yi вокруг регрессионной прямой и разброса хi на стандартную ошибку. Чем сильнее меняется наклон прямой, тем больше разброс значений свободного члена. Кроме того, дисперсия и стандартная ошибка свободного члена тем больше, чем больше средняя величина х2i. При больших по модулю значениях х даже небольшое изменение наклона регрессионной прямой может вызвать большое изменение оценки свободного члена, поскольку в этом случае в среднем велико расстояние от точек наблюдений до оси у.
3.3. Нелинейная регрессия
Зависимость многих экономических показателей не линейна. Метод наименьших квадратов не предназначен для оценки параметров нелинейных регрессий, кроме полиномиальной. Однако целый класс нелинейных зависимостей можно привести к зависимостям линейным преобразованием независимой и/или зависимой переменной. Такое преобразование называется линеаризацией.
Задача построения нелинейной модели регрессии состоит в следующем
Задана нелинейная спецификация модели
y = f(x,a,b,),
где y - зависимая, объясняемая переменная; x - независимая, объясняющая переменная; a, b - параметры модели, для которых должны быть получены оценки; - аддитивный или мультипликативный случайный фактор.
Требуется
1. Преобразовать исходные данные х х*, у у* так, чтобы спецификация модифицированной регрессии была линейной:
y* = a* + b*x*
2. Методом наименьших квадратов получить оценки параметров a*, b*.
3. По оценкам a*, b* вычислить искомые оценки параметров a, b исходной регрессии.
Способы преобразования данных и вычисления параметров a, b по оценкам a*, b* приведены в следующей таблице.
|
Исходная спецификация |
Преобра-зование х х* |
Преобра-зование у у* |
Вычисление b по b* |
Вычисление a по a* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|