4.8. Модели авторегрессии стационарных временных рядов и их идентификация

4.8.1. Основные понятия

Необходимо формировать такие модели нерегулярной компоненты (t), которые бы позволили формировать прогнозы их значений по уже известным значениям (t) в предыдущие моменты времени в отличие от классической регрессионной модели, в которой по известным значениям спецификация полностью определена, а будущие значения вычисляются простой подстановкой в модель времени t.

Такие модели, в которых прогноз будущих значений формируется по предыдущим, называются авторегрессионными.

Стационарный временной ряд (t) называется «белым шумом», если

M(t) = 0,                                                                      

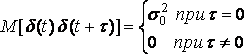
Таким образом, при любом сколь угодно малом  значения (t), (t+) независимы.

4.8.2. Модель авторегрессии 1-го порядка

Достаточно большой класс стационарных временных рядов, имеющих смысл нерегулярной компоненты экономического временного ряда, могут быть представлены следующим образом

(t) = (t – 1) + (t),  (3)

где || < 1.

Из представления (3) следует, что (t) формируется только на основе предыдущего значения (t–1) и не зависит от всех прошлых. При этом на значение (t) влияние текущее значение возмущения (t).

Процессы авторегрессии 1-го порядка также называются марковскими.

Для марковских процессов доказано, что

1) M(t) = 0,

2) K() = ^,

Таким образом, большое положительное (близкое к 1) значение  означает сильную коррелированность значений временного ряда, отстоящих на небольшое значение , и медленное затухание этой зависимости с ростом . Временной ряд при таких  имеет более плавный характер. При малом значении  степень зависимости значений временного ряда быстро уменьшается. При этом ряд имеет более изрезанный «дёрганный характер».

K(1) = ,

то есть величина  – это коэффициент корреляции соседних значений временного ряда.

3) 

Из последнего соотношения следует, что, если значение || близко к 1, тогда дисперсия (t) будет значительно больше дисперсии возмущения (t). То есть, если соседние значения ряда (t) сильно коррелированны, то ряд довольно слабых возмущений (t) будет порождать размашистые колебания остатков (t).

Из соотношения

K(1) = ,

следует способ идентификации модели авторегрессии 1-го порядка.

Оценка величины  формируется как оценка корреляционной функции в точке 1:

.

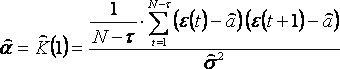4.8.3. Модель авторегрессии второго порядка

(t) = ₁(t – 1) + ₂(t – 2) + (t).

Условие стационарности (t):

|₁| < 2,

₂ < 1 – |₁|.

Доказано, что

;

;

на основе этих соотношений строятся оценки параметров ₁, ₂.

Для корреляционных функций процессов авторегрессии 2-го порядка уже не удаётся получить аналитическое выражение для корреляционной функции, однако существует рекуррентный алгоритм вычисления всех значений:

K() = ₁K( – 1) + ₂K( – 2).

²₀ = ² – ₁K(1) – ₂K(2).

4.8.4. Оценивание параметров моделей авторегрессии. Метод инструментальных переменных.

При построении моделей авторегрессии:

у_t=a + b₀  x_t + c₁  y_t-1 + u_t

возникает проблема: нарушается 1-я предпосылка нормальной линейной модели регрессии об отсутствии связи между факторным признаком и случайной составляющей. В модели авторегрессии факторный признак у_t-1 связан со случайной составляющей u_t-1. Поэтому применение обычного МНК для оценки параметров уравнения регрессии приводит к получению смещенной оценки параметра при переменной у_t-1.

Для оценивания параметров уравнения регрессии может быть использован метод инструментальных переменных.

Суть метода инструментальных переменных состоит в следующем.

Переменную у_t-1 из правой части уравнения, для которой нарушается предпосылка МНК, заменяют на новую переменную, удовлетворяющую следующим требованиям:

1)         она должна тесно коррелировать с  у_t-1;

2)         она не должна коррелировать со случайной составляющей u_t.

Затем оценивают регрессию с новой инструментальной переменной с помощью обычного МНК.

Рассмотрим один из методов получения инструментальной переменной. Так как у_t зависит от х_t, предположим, что имеет место зависимость у_t-1 от х_t-1, т.е. 

Оценка  может быть найдена с помощью обычного МНК.

Новая переменная  тесно коррелирует с у_t-1 и не коррелирует со случайной составляющей u_t, т.е. может служить инструментальной переменной для фактора у_t-1.

В результате модель авторегрессии примет вид:

().

Оценки параметров данной модели находят обычным МНК. Полученные оценки являются искомыми оценками модели авторегрессии.

Отметим, что практическая реализация метода инструментальных переменных осложняется появлением проблемы мультиколлинеарности факторов в модели: функциональная связь между  и х_t-1 () приводит к появлению высокой корреляционной связи между  и x_t. В некоторых случаях эту проблему можно решить включением в модель фактора времени t.