3.2. Линейная парная регрессия

3.2.1. Определения

Парной линейной регрессией называется зависимость

выборочного условного математического ожидания от переменной х. Термин «парная» означает зависимость двух переменных Y, X. Термин «линейная» означает их линейную зависимость.

Условное выборочное математическое ожидание – это выборочное среднее значение величины Y при условии, что переменная X приняла значение х.

Модель наблюдения

,

b₀ – оценка свободного члена ₀,

b₁ – оценка углового коэффициента ₁.

3.2.2. Принцип, метод наименьших квадратов

Согласно принципу наименьших квадратов неизвестные параметры b₀, b₁ выбираются таким образом, чтобы была минимальна сумма квадратов невязок или остатков

.

Следует отметить, что для оценки параметров b₀, b₁ возможны и другие подходы. Например, можно находить эти параметры при минимизации суммы абсолютных величин невязок . Однако вычислительные процедуры, соответствующие принципу наименьших квадратов существенно проще. Эти вычислительные процедуры получили название «Метод наименьших квадратов» (МНК).

Исходя из необходимого условия экстремума функции двух переменных S(b₀,b₁) приравниваем к нулю её частные производные

;

;

откуда после преобразований получим систему нормальных уравнений для определения параметров линейной регрессии:

Теперь разделим обе части уравнений на n, получим систему нормальных уравнений в виде

;

,

где 

Подставляя значение

из первого уравнения системы в уравнение регрессии, получим

;

Коэффициент b₁ называется выборочным угловым коэффициентом регрессии У по Х.

Коэффициент b₁ показывает, на сколько единиц в среднем изменяется выборочное условное среднее при увеличении переменной Х на одну единицу.

Из нормальной системы получаем

,

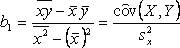где s_x² – выборочная дисперсия переменной Х;

– выборочная ковариация величин X,Y;

величину b₀ можно найти через коэффициент b₁:

.

Через коэффициент b₁ также можно выразить выборочный коэффициент корреляции

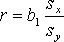
3.2.3. Свойства оценок параметров парной линейной регрессии

Для того чтобы полученные МНК оценки а и b обладали желательными свойствами, необходимо, чтобы выполнялись следующие условия:

1) величина _i, является случайной переменной;

2) математическое ожидание _i равно нулю: М(е) = 0;

3) дисперсия _i постоянна: D(_i) = D(_i) = а² для всех i;

4) значения _i независимы между собой.

По теореме Гаусса-Маркова

если условия 1)-4) выполняются, то оценки, сделанные с помощью МНК, обладают следующими свойствами:

1) Оценки являются несмещенными, т.е. математическое ожидание оценки каждого параметра равно его истинному значению: М(b₀) = ₀; М(b₁) = ₁. Это вытекает из того, что М(_i)=0, и говорит об отсутствии систематической ошибки в определении положения линии регрессии.

2) Оценки состоятельны, так как дисперсия оценок параметров при возрастании числа наблюдений стремится к нулю: limD(b₀) = 0; limD(b₁) = 0. Иначе говоря, если п достаточно велико, то практически наверняка b₀ близко к ₀, ab₁ близко к ₁: надежность оценки при увеличении выборки растет.

3) Оценки эффективны, они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра, линейными относительно величин у_i. В англоязычной литературе такие оценки называются BLUE (BestLinear Unbiased Estimators - наилучшие линейные несмещенные оценки).

Перечисленные свойства не зависят от конкретного вида распределения величин _i, тем не менее обычно предполагается, что они распределены нормально N(0;y²). Эта предпосылка необходима для проверки статистической значимости сделанных оценок и определения для них доверительных интервалов. При ее выполнении оценки МНК имеют наименьшую дисперсию не только среди линейных, но среди всех несмещенных оценок.

Если предположения 3) и 4) нарушены, то есть дисперсия возмущений непостоянна и/или значения _i связаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности - нет.