Задачи для самостоятельного решения.

Задана нелинейная спецификация модели

y = f(x,a,b,),

где y - зависимая, объясняемая переменная; x - независимая, объясняющая переменная; a, b - параметры модели, для которых должны быть получены оценки;  - аддитивный или мультипликативный случайный фактор.

Требуется

1.         Преобразовать исходные данные х  х*, у   у* так, чтобы модифицированная регрессия(спецификация) была линейной: y* = a*x* + b*.

2.         Методом наименьших квадратов получить оценки параметров a*,  b*.

3.         По оценкам a*,  b* вычислить искомые оценки параметров a, b исходной регрессии.

Варианты задач

Вариант 1			Вариант 2								Вариант 3
y=b+a/x+e, a>0			y=b+a/x+e, a<0									y=1/(b+ax+e)
X	Y		X				Y				X			Y
0,916292786	2,343363505		0,8754701				-1,26416				0,8554965			0,449422
1,96776321	1,254419585		1,71458982				-0,14667				1,9269758			0,30483
2,927757642	0,840675808		3,21629606				0,423662				3,2220226			0,163384
4,075754243	0,711689435		4,29114476				0,488321				4,0471988			0,13331
5,079008984	0,584852629		4,57218017				0,521846				5,1965291			0,106708
5,922022819	0,561834353		5,52632472				0,662738				6,0097174			0,118901
7,034135167	0,555505126		7,36311137				0,761182				7,0891826			0,114027
8,033758859	0,438769487		8,16170418				0,785765				8,0076095			0,119111
9,021557157	0,383531491		9,21670881				0,733856				8,8652203			0,097962
9,940281582	0,35673309		9,54617082				0,805989				10,193225			0,100949
11,0485224	0,364696832		11,218714				0,841907				10,784798			0,072188
12,04614621	0,403594817		12,1501452				0,814111				11,993337			0,063631
13,0913511	0,353969121		13,1276866				0,869817				13,170309			0,058044
14,06678827	0,316563563		14,2371927				0,827654				14,246495			0,064075
15,08004542	0,305715214		15,3580428				0,824779				15,215612			0,054045
15,91655332	0,251197241		16,1246149				0,88135				16,110331			0,050658
16,94457031	0,375252251		16,931787				0,911042				16,859436			0,049641
17,97281252	0,340207852		18,3341632				0,893731				17,871849			0,049417
19,08744601	0,346897736		18,9035464				0,888224				19,22026			0,052684
20,06500789	0,371743311		20,2874912				0,867629				20,077762			0,049665
Вариант 4			Вариант 5									Вариант 6
y=x/(b+ax+xe), b<0			y=beax+, a>0									y=beax+, a<0
X	Y		X				Y				Х			У
0,70420704	0,63955744		11,6396592				4,198294				0,5366679			2,476816917
0,89923496	0,54089936		21,6591799				5,322306				2,1629918			2,148240118
1,09888702	0,46827711		29,1876072				4,401264				5,6388971			1,48530221
1,29707832	0,45920069		40,3866137				5,100606				6,6146724			0,720592743
1,49528961	0,42137335		50,7178631				7,306009				6,0234452			0,980893256
1,6981285	0,40428899		61,0099721				7,35836				8,3310035			0,847704349
1,89728299	0,41258312		67,672226				7,862084				11,941435			0,69897142
2,1033694	0,38231339		77,60817				9,336061				13,424995			0,440162518
2,29960467	0,39186135		89,597099				9,166467				14,966856			0,416734365
2,50444049	0,37504088		101,146367				10,59379				18,857232			0,300226709
2,69922199	0,37496435		108,643187				12,63302				17,876686			0,242781254
2,90475386	0,37768223		122,25779				13,38357				20,195971			0,215156615
3,10047027	0,37075987		128,751711				16,49389				23,728978			0,167938169
3,29967405	0,36672255		139,348075				14,28992				28,313203			0,10080251
3,49606573	0,35425163		152,431781				16,39134				27,86847			0,110097072
3,69843332	0,38441035		158,473867				16,49684				28,815883			0,15055619
3,90438351	0,35441752		168,614341				26,37435				31,888705			0,06017931
4,10321173	0,34595593		177,931078				28,1961				33,174267			0,09264964
4,30211311	0,34304271		190,000015				29,44732				36,903934			0,039875002
4,49944876	0,3662169		199,128989				34,0054				38,042099			0,041178868
Вариант 7					Вариант 8
y=			y=bxae
X	Y		X				Y
-0,00252	0,166794139		0,009794792				0,14078981
0,443184	0,249817398		0,459925478				1,16110718
0,876557	0,331910788		0,910385205				1,61777144
1,333027	0,39546292		1,359584249				1,8328449
1,824995	0,591862697		1,809630841				1,79206784
2,249678	0,725425424		2,259900787				2,11692549
2,655618	0,703094349		2,7104565				3,00795428
3,100252	0,837453134		3,159862068				2,25212249
3,647639	0,726742863		3,61036957				2,58588532
4,036611	0,90607963		4,060197961				3,52239107
4,530949	0,904472473		4,510194061				3,29816294
4,919404	0,978331982		4,959930223				3,2486891
5,437894	0,995397311		5,409966221				4,20983394
5,832266	1,007182224		5,860071196				4,31512473
6,254228	0,881896314		6,310487825				3,97940274
6,744444	1,056702531		6,759799248				3,36234716
7,153382	1,250786629		7,209525218				4,67512974
7,637258	0,946742301		7,659749875				3,73258773
8,086705	1,113236265		8,109978847				5,15949126
8,502151	0,972237843		8,560343099				4,02303078

Проверка гипотезы о наличии тренда во временном ряде. Методы сглаживания временного ряда.

Краткое изложение используемых методов решения и основных теоретических положений

Проверка гипотезы стационарности временного ряда - начальный этап сглаживания. Даны значения временного ряда x(1), x(2),..., x(n). Необходимо определить, имеет ли этот ряд неслучайную компоненту, зависящую от времени - тренд.

Пусть x_med - выборочная медиана этого временного ряда. Образуем ряд z(1), z(2),..., z(n) следующим образом:

z(i) = знак(x(i) - x_med).

Серия - это группа подряд идущих +1 или -1. Обозначим (n) - количество серий; (n) - длина самой протяжённой серии.

Критерий, основанный на выборочной медиане состоит в следующем:

если выполняются оба неравенства

,

,

тогда с вероятностью, заключённой между 0,9025 и 0,95 делается вывод о неизменности среднего значения ряда и об отсутствии тренда. Если хотя бы одно из неравенств не выполняется, тогда с такой же вероятностью следует сделать вывод о наличии тренда.

После того, как установлено, что временной ряд имеет тренд, необходимо выделить этот тренд. Процедура  выделения тренда временного ряда называется сглаживанием. Выделение тренда из временного ряда эквивалентно удалению нерегулярной, случайной компоненты временного ряда, после чего этот ряд приобретает «гладкий» вид. По этой причине выделение тренда называется сглаживанием.

Методы выделения тренда (сглаживания) можно условно разделить на два типа:

1)             аналитические,

2)             алгоритмические.

Аналитические методы основаны на допущении, что известен общий вид, спецификация неслучайной составляющей. Например, тренд ряда может иметь линейную спецификацию

f(t) = ₀ + ₁t..

Тогда задача выделения тренда сводится к построению оценок  для параметров ₀, ₁. Эти методы называются аналитическими, потому что позволяют получить аналитическое выражение тренда.

Алгоритмические методы не используют предположение о виде тренда, поэтому имеют более широкую область применения. Алгоритмические методы заключаются в выработке алгоритма, способа расчёта значения величины тренда для любого заданного момента времени.

Аналитические методы

Временной ряд представляется в виде модели регрессии

x(t) = f(t;) + (t), t = 1, 2, …, n.

Далее применяются методы регрессионного анализа для получения вектора оценок .

Метод скользящего среднего

В основном методы алгоритмического сглаживания – это различные модификации скользящего среднего.

В основе этих методов лежит следующее соображение: если индивидуальный разброс значений временного ряда x(t) вокруг тренда f(t) характеризуется дисперсией ², то разброс среднего из N членов временного ряда (x(1) +x(2) +…+ x(N))/N около того же значения будет характеризоваться дисперсией ²/N.

Алгоритм скользящего среднего заключается в следующем:

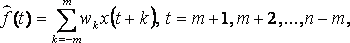
где w_k – некоторые весовые коэффициенты, в сумме равные 1, т.е.

.

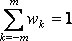Поскольку, изменяя t от m+1 до n-m диапазон суммирования скользит по временному ряду (при переходе от t к t+1 в составе слагаемых происходит замена только одного слагаемого x(t – m) слагаемым x(t + m + 1)), то и методы, основанные на формуле (1) называются методами скользящего среднего (МСС).

Один МСС отличается от другого выбором параметров m и весов w_k.

Веса определяются из следующей таблицы

m	веса
1	1/3, 1/3, 1/3 (средняя арифметическая)
2	-3/35, 12/35, 17/35, 12/35, –3/35
3	–2/21, 3/21, 6/21, 7/21, 6/21, 3/21, –2/21

Метод экспоненциально взвешенного скользящего среднего (метод Брауна)

Методы скользящего среднего основываются на том, что все значения временного ряда имеют одинаковую информационную ценность. Однако в задачах прогноза, в которых сглаженная функция  используется обычно для формирования прогнозов на несколько тактов вперёд, недавние значения x(t) очевидно ценнее, чем значения ряда в далёком прошлом, так как ряд далее будет вести себя так, какова сформировавшаяся тенденция в настоящем и недалёком прошлом.

Эта идея реализована в методе экспоненциально взвешенного скользящего среднего Брауна

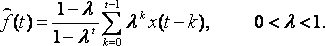
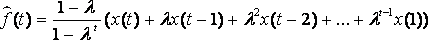
Таким образом, значения временного ряда тоже сглаживаются, однако существуют следующие отличия от обычного МСС

1)         скользит только правый край интервала усреднения(левый край закреплён в точке t = 1)

2)         веса при x(t – k) экспоненциально уменьшаются по мере «удаления в прошлое»,

3)         формула (2) даёт оценку сглаженного значения временного ряда не в средней, а в правой, конечной точке усреднения,

4)         нет проблемы крайних значений.

Дисперсия остаточной случайной компоненты после сглаживания

,

где  - остаточная нерегулярная компонента после сглаживания.

² = Dx(t);

поэтому при значениях , не слишком близких к 1, и для достаточно удалённых от прошлого значений t случайные остатки  подвержены существенно меньшему разбросу.

Рекуррентный способ вычисления сглаженных значений .

;
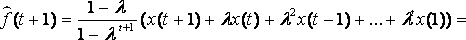
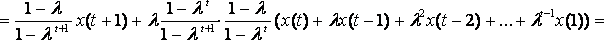
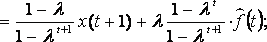
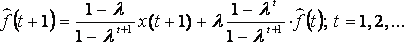