
mat_analiz
.pdf§ 9. Производные и дифференциалы высших порядков
Пусть функция y = f (x) имеет производную в каждой точке некоторо-
го множества Х. Тогда, как уже указывалось выше, производная этой функции, рассматриваемая на множестве Х, представляет собой функцию аргумента x.Эта функция также может иметь производную. Производная от
′ |
|
|
|
|
|
|
|
|
f (x ) (если она существует) называется производной второго порядка или |
||||||||
второй производной от функции |
f (x) и обозначается одним из символов: |
|||||||
|
|
d 2 y |
|
|
|
′ |
||
′′ |
′′ |
|
|
|
′ |
′ |
) . |
|
dx 2 . Таким образом, по определению y |
||||||||
y , f |
(x ), |
|
= (y |
|||||
Если существует производная от второй производной, то ее называют производной третьего порядка или третьей производной от функции f (x) и обо-
|
|
d 3 y |
|
|
|
′ |
||
′′′ |
′′′ |
|
|
′′′ |
= (y |
′′ |
) |
|
dx 3 . Итак, по определению y |
||||||||
значают однимизсимволов: y , |
f (x ), |
|
|
|||||
Аналогично от производной третьего порядка можно перейти к производной четвертого порядка и т.д.
Производную от производной (n −1)-го порядка (если она существует)
называют производной n -го порядка или n -ой производной. Для обозначения используются символы:
y (n ), f (n )(x ), |
d n y |
. |
|
||
|
dx n |
|
Таким образом, по определению
y (n ) = (y (n−1))′.
Производные, начиная с производной второго порядка, называются производными высших порядков.
Иногда для обозначения производных высших порядков используются
символы: |
′′ |
′′′ |
и т. д. |
yxx , |
y xxx |
||
Отметим, |
что y′ называют также производной первого порядка или |
||
первой производной.
157

Пример 34. Дана функция y = x 6 +ln x. Найти y (4).
Решение. y′ = 6x |
5 |
1 |
, y′′ |
= 30x |
4 |
|
|
1 |
, y′′′ =120x |
3 |
2 |
|
|||||
|
+ |
|
|
− |
|
|
+ |
|
, |
||||||||
|
x |
|
x 2 |
|
x 3 |
||||||||||||
y (4) |
= 360x 2 − |
|
6 |
, или |
y |
(4) = |
6(60x 6 −1). |
|
|||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
x 4 |
|
|
|
|
|
x 4 |
|
|
|
|
|
Замечание 12. Можно показать, что если материальная точка движется |
|||||||||||||||||
прямолинейно и функция S = f (t )-закон этого движения, то f ′′(t0 ) представ-
ляет собой ускорение движущейся точки в момент времени t0 . В этом состо-
ит механический смысл второй производной.
Рассмотрим теперь дифференциалы высших порядков.
Пусть на множестве Х задана функция y = f (x ), х – независимая пере-
менная. Дифференциал dy = f ′(x )dx данной функции является функцией от х
(заметим, что при этом дифференциал dx независимой переменной х рассматривается как величина, не зависящая от х). Рассмотрим дифференциал от этой функции, то есть дифференциал от dy как функции независимой переменной х (при этом считаем значение dx дифференциала независимой переменной тем же самым). Этот дифференциал называют дифференциалом второго порядка или вторым дифференциалом от функции y = f (x).
Таким образом, дифференциал второго порядка или второй дифференциал функции y = f (x) определяется как дифференциал от дифференциала данной функции и обозначается символом d 2 y.
Итак, d 2 y = d (dy).
Аналогично, дифференциалом третьего порядка или третьим дифференциалом функции y = f (x) называется дифференциал от дифференциала второго порядка этой функции (при этом значение dx считаем тем же самым).
Обозначается символом Итак, d 3 y = d (d 2 y ).
От дифференциала третьего порядка можно перейти к дифференциалу четвертого порядка и т.д.
158
Дифференциалом n -го порядка или n -ым дифференциалом функции y = f (x) называется дифференциал от дифференциала (n −1)-го порядка этой функции (при этом значение dx считаем тем же самым). Обозначается симво-
лом d n y.
Таким образом, d n y = d (d n−1 y ) (n >1).
Подчеркнем, что определяя дифференциалы высших порядков, дифференциал независимой переменной все время рассматриваем как постоянную величину. Учитывая это, будем иметь:
|
d |
2 |
|
|
′ |
|
′ |
′′ |
|
′′ |
|
2 |
; |
|
|
|
|
|
y = d (dy )= (y dx ) dx = y dx dx = y dx |
|
|
|
|||||||||||
d |
3 |
y |
= d (d |
2 |
′′ |
2 |
′ |
′′′ |
2 |
|
′′′ |
|
|
3 |
. |
|
|
|
y )= (y dx |
|
) |
dx = y dx |
dx = y dx |
|
|||||||||
Методом математической индукции можно доказать, что для любого натурального n справедлива формула:
d n y = y (n )dx n . |
(13) |
(При этом предполагаем, что существуют соответствующие производные.)
Здесь символы dx 2 , dx 3 , dx n обозначают соответствующие степени
dx , то есть (dx )2 , (dx )3 , |
(dx )n . |
|
|
|
|
|
|
|
Из равенства (13) получаем |
|
|
|
|
|
|
|
|
|
y |
(n ) |
= |
d n y |
, |
|||
|
|
|
dxn |
|||||
|
|
|
|
|
|
|||
то есть приведенный ранее символ |
d n y |
|
для обозначения производной n -го |
|||||
|
dxn |
|||||||
|
|
|
|
|
|
|||
порядка можно рассматривать как дробь. |
|
|
||||||
Пример35. Дана функция y = x 5 −5x 3 + 4. Найти d 4 y. |
||||||||
Решение. Согласно формуле (13) имеем: |
||||||||
|
d 4 y = y(4)dx4 . |
|||||||
Так как y′ = 5x4 |
−15x2 , y′′ = 20x3 |
−30x, y′′′ = 60x2 −30, y(4 ) =120x, то |
||||||
окончательно получаем |
d 4 y =120x dx 4 . |
|
|
|
|
|||
159
При рассмотрении в § 8 дифференциала функции, было отмечено, что он обладает свойством инвариантности формы: если y = f (x), то dy = f ′(x )dx ,
независимо от того, является ли x независимой переменной, или же x −функция другой переменной. Дифференциалы же высших порядков этим свойством не обладают. Таким образом, формула (13) при n >1 справедлива, вообще говоря, только в том случае, когда x - независимая переменная. Если же x - функция некоторой другой переменной, то эта формула в общем случае неверна.
Рассмотрим, например, дифференциал второго порядка функции y = f (x ). Выше показано, что если x - независимая переменная, то
(14)
Пусть теперь x не является независимой переменной, то есть x =ϕ(t ).
Тогда dx = ϕ′(t )dt и, следовательно, dx уже нельзя считать постоянной. В этом случае, используя правило вычисления дифференциала произведения, получим
|
|
|
d |
2 |
′ |
|
|
′ |
dx |
+ y |
′ |
|
|
′′ |
2 |
′ 2 |
x. |
|
|
|
|
|
y = d (dy )= d (y dx )= dy |
|
|
d (dx )= y dx |
+ y d |
||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 |
|
′′ |
2 |
|
|
′ |
2 |
x. |
|
|
(15) |
|
|
|
|
|
|
|
y = y dx |
+ y d |
|
|
|
||||||||
Сравнивая (14) и (15), замечаем, что в последнем случае появилось сла- |
||||||||||||||||||
гаемое |
′ |
2 |
x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ясно, что для d 2 y равенство (15) является более общим, так как в том
случае, когда x - независимая переменная, имеем d 2 x = 0 , а следовательно, второе слагаемое в равенстве (15) равно нулю, тем самым получаем формулу (14).
Пример 36. Дана функция y = 2x3 − 4x2 + 7x . Найтиd 2 y
а) при условии, что x -независимая переменная;
б) при условии, что x -функция от другой независимой переменной.
Решение. а) Так как y′ = 6x 2 −8x + 7, y′′ =12x −8 , то d 2 y = (12x −8)dx 2 .
160
б) В этом случае пользоваться формулой (13) нельзя. Следует использовать правило вычисления дифференциала произведения.
Получаем:
d 2 y = d (dy )= d |
(2x 3 |
− 4x 2 |
+ 7x )′dx |
= d ((6x 2 |
−8x + 7)dx )= d (6x 2 −8x + 7) dx + |
|
|
|
|
|
|
+ (6x 2 −8x + 7) d (dx )= (6x 2 −8x + 7)′ dx dx + (6x 2 −8x + 7)d 2 x = (12x −8)dx 2 + + (6x 2 −8x + 7)d 2 x.
Задания для самостоятельной работы
1. Найти производные второго порядка следующих функций:
а) |
y = x 3 +ln x ; |
б) |
y = ex4 ; |
в) y = sin 2 (2x +5); |
г) y = x +3 |
x + 2 . |
|||
2. |
Доказать, |
что для функции |
y = e2x (3x −1)справедливо равенство |
||||||
y′′− 4y′+ 4y = 0 . |
|
|
|
|
|
|
|
|
|
3. Найти производные третьего порядка следующих функций: |
|
||||||||
а) |
y = x 4 −8x 2 −7x +10; |
б) x = sin |
t |
; в) |
y = e5−2x ; г) y =ln |
cosx. |
|
||
|
|
||||||||
|
|
|
|
4 |
|
|
|
|
|
4. |
Материальная |
точка |
|
движется прямолинейно по |
закону |
||||
S (t )= t 3 + 2t 2 +t, где S - путь (в метрах), t - время (в секундах). Найти ускоре-
ние движущейся точки через 2 секунды после начала движения.
5. Найти дифференциал второго порядка для следующих функций:
а) y = 5 x2 ; б) y = ctg x ( x -независимая переменная).
Ответы: 1. а)
г) y |
′′ |
2 |
|
= − 9(x + 2) 3 |
|||
|
3. а) y′′′ = 24x ; б)
5. а) d 2 y = − |
6 |
25x 5
y |
′′ |
= |
|
6x 3 −1 |
; |
|
б) |
y |
′′ |
= |
4x |
2 |
e |
x 4 |
(4x |
4 |
+3); |
|
в) |
y |
′′ |
= 8cos(4x +10); |
||||||||||||
|
x 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
(x + 2)2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
′′′ |
|
1 |
|
|
|
|
t |
|
|
|
|
|
′′′ |
|
|
|
|
5−2x |
|
|
′′′ |
|
sin x |
|
|
м |
|
|||||
|
x |
= − 64 cos 4 ; |
|
в) |
y |
= −8e |
|
|
; г) y |
= − cos3 x . |
4. 16 c . |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
dx 2 ; |
|
б) |
d 2 y = |
|
2 cos x |
dx 2 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 3 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
161

§10. Дифференцирование параметрически заданных функций
Пусть функции x = ϕ(t) и y = Ψ(t) определены в некоторой окрестности точки t0 , причем функция x = ϕ(t) непрерывна и строго монотонна в указан-
ной окрестности. Тогда существует обратная к x = ϕ(t) функция t = χ(x) , и в некоторой окрестности точки x0 =ϕ(t0 ) определена функция y от x:
y= Ψ[χ(x )].
Втаком случае говорят, что эта функция y от x задана параметрически уравнениями x = ϕ(t) , y = Ψ(t) . Обозначим эту функцию так: y = Φ(x) .
Если функции x = ϕ(t) и y = Ψ(t) в точке t0 имеют производные и
ϕ'(t0 ) ≠ 0 , то функция y = Φ(x) имеет производную в точке x 0 =ϕ(t 0 ) , причем
Φ′(x0 ) = Ψ′′(t0 ) ,
ϕ(t0 )
или кратко (используя другие обозначения производной и опуская обозначение аргумента)
y′x |
= |
yt′ |
. |
|
|||
|
|
x t′ |
|
Покажем справедливость приведенного утверждения. Действительно, применяя правило дифференцирования сложной функции и правило дифференцирования обратной функции, получаем:
|
|
|
|
|
y ′x = y t′ t x′ = y t′ |
1 |
= |
|
y t′ |
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x t′ |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x t′ |
|
|
|
|
|
|
|
|
|
|
Рассмотрим теперь вычисление второй производной. |
|
|
|
||||||||||||||||||||||||||
Если кроме указанных выше условий существуют x tt′′ (t0 ) и ytt′′ (t0 ) , то |
|||||||||||||||||||||||||||||
существует и y′xx′ |
(x 0 ) , причем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
y′ |
|
|
′ |
y′′x′ |
− x′′y′ |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
tt |
t |
|
|
tt t |
|
|
|
|
||||
|
|
|
|
y′ ′ |
|
|
|
|
xt′ |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
y′′x′ − x′′y′ |
|
||||
′′ |
′ |
′ |
t |
|
= |
|
|
|
= |
|
|
|
(x′) |
= |
|
|
|||||||||||||
|
t |
′ |
|
|
|
t |
|
|
|
|
t |
|
tt t |
tt |
t |
|
|||||||||||||
y xx = (y x |
)x |
= |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
xt′ |
|
|
|
|
|
|
|
xt′ |
|
|
|
|
|
3 |
|
|
|||||||||
|
|
|
|
xt′ t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(xt′) |
|
|
|
|||||
Поступая аналогично, можно вычислить y′xxx′′ |
|
и т. д. |
|
|
|
|
|||||||||||||||||||||||
162
Пример 37. Функция y от x задана параметрически уравнениями:
x =t −sin t, y =1−cost , (−∞ < t < +∞). Найдем y x и y xx . |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
′′ |
|
|
|
|
|
|||
Решение. Имеем: x t′ =1 −cos t, |
yt′ = sin t , |
|
причем x t′ ≠ 0 при t ≠ 2kπ |
||||||||||||||||||||
( k = 0,±1,±2,... ). Следовательно, если t ≠ 2kπ , то |
|
|
|
|
|
|
|
||||||||||||||||
|
|
yt′ |
|
|
sin t |
|
|
2 sin |
t |
|
cos |
t |
|
|
t |
|
|
|
|
||||
y′x |
= |
= |
|
= |
2 |
2 |
|
= ctg |
|
; |
|
||||||||||||
x t′ |
1 − cost |
2 sin 2 |
t |
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
t |
′ |
|
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ctg |
|
|
|
|
2 sin |
2 t |
1 |
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||
y′′xx |
= |
|
t = |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
= − |
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
||||||||||||
|
|
|
xt′ |
|
|
2sin 2 |
|
|
t |
|
4sin 4 |
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задания для самостоятельной работы
1. Найти y′x и y′xx′ для функций, заданных параметрически уравнениями:
а) x = t, y = t 3 ; б) x = sin t, y = sin 2t .
2.Найти угловой коэффициент касательной, проведенной к эллипсу
x= a cost, y = bsin t в точке, для которой t = π6 .
3.Функция задана параметрически уравнениями: x = et , y = 2e −t . Соста-
вить уравнение касательной, проведенной к графику этой функции в точке М, для которой t = 0.
Ответы: 1. а) |
′ |
|
2 |
|
′′ |
′ |
|
2 cos 2t |
|
′′ |
|
3 |
|
yx |
= 3t |
|
, |
y xx |
= 6t. б) yx |
= |
|
, |
y xx |
= −2(tg |
|
t + 3 tgt ). |
|
|
cost |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. k = − |
3b . |
|
|
|
3. 2x + y −4 = 0 . |
|
|
|
|
|
|||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
§ 11. Основные теоремы дифференциального исчисления
Рассмотрим теоремы, которые ввиду их важности, называют основными теоремами дифференциального исчисления.
Теорема 4 (теорема Ферма). Пусть функция y = f (x) определена на промежутке X и во внутренней точке x0 этого промежутка принимает наи-
большее или наименьшее значение. Тогда, если в точке x0 существует произ-
водная, то она равна нулю.
163
Доказательство. Предположим для определенности, что функция y = f (x) в точке x0 принимает наибольшее значение. Тогда
|
∆y = f (x0 + ∆x)− f (x0 )≤ 0 |
|
|
||||||||||||
для любой точки x0 + ∆x X . Следовательно, если ∆x > 0, то |
∆y |
≤ 0; если же |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x |
|
∆x < 0, то ∆y |
≥ 0. Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
||
∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
∆y |
|
≥ 0 и |
lim |
|
∆y |
|
≤ 0 . |
|
(16) |
||||
|
|
|
|
|
|
|
|||||||||
|
∆x →0− ∆x |
|
|
∆x →0+ ∆x |
|
|
|
|
|
|
|||||
По условию теоремы функция y = f (x) |
в точке x0 имеет производную. |
||||||||||||||
Значит |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ′(x 0 )= lim |
∆y |
= |
lim |
∆y |
|
= lim |
∆y |
. |
|
(17) |
||||
|
|
∆x |
|
|
|||||||||||
|
∆x →0 |
∆x |
∆x →0− |
|
∆x →0+ ∆x |
|
|
||||||||
Из (16) и (17) вытекает, что f ′(x 0 )= 0.
Аналогично рассматривается случай, когда функция y = f (x) в точке x0
принимает наименьшее значение.
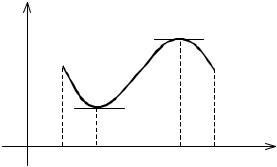
Геометрический смысл теоремы Ферма заключается в том, что если функция y = f (x) во внутренней точке x0 промежутка X принимает наи-
большее или наименьшее значение и дифференцируема в этой точке, то касательная, проведенная к графику этой функции в точке (x0 , f (x0 )), параллельна оси Ox (рис. 5).
y
0 |
x 0 |
x |
Рис. 5
164
Теорема 5 (теорема Ролля). Пусть функция y = f (x)
1)непрерывна на [a,b];
2)дифференцируема на (a,b);
3)принимает равные значения на концах отрезка, то есть f (a)= f (b).
Тогда существует хотя бы одна такая точка c (a,b), что Доказательство. Поскольку y = f (x) непрерывна на [a,b], то она
принимает на этом отрезке свое наибольшее значение и свое наименьшее значение. Обозначим их соответственно M и m . Рассмотрим два возможных случая:
1. M = m . Тогда функция на отрезке [a, b] сохраняет постоянное значе-
ние. А поэтому f ′(x )= 0 в любой точке рассматриваемого промежутка. Таким
образом, в качестве c можно взять любую точку, принадлежащую интервалу
(a,b).
2. M > m . Поскольку по условию теоремы f (a)= f (b), то по крайней ме-
ре одно из значений M или m функция принимает в некоторой точке
c (a, b). А тогда согласно теореме Ферма f |
(c)= 0. |
|
′ |
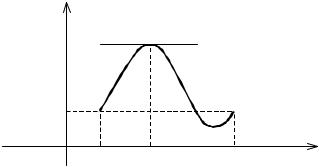
Геометрический смысл теоремы Ролля состоит в следующем: если функция y = f (x) непрерывна на [a,b], дифференцируема на (a,b) и на концах отрезка [a,b] принимает равные значения, то найдется хотя бы одна точка c (a,b), такая, что касательная, проведенная к графику данной функции в точке (c; f (c)), параллельна оси Ox (рис.6).
y
f(a)=f(b) |
|
|
|
|
0 |
a |
c |
b |
x |
|
|
Рис. 6 |
|
|
165
Теорема 6 (теорема Лагранжа). Пусть функция y = f (x) непрерывна на
[a,b] и дифференцируема на (a,b).
Тогда найдется такая точка c (a,b), что выполняется равенство
f (b)− f |
(a) |
|
′ |
|
|
|
|
|
= |
f (c). |
(18) |
b − a |
|
|
|||
|
|
|
|
|
|
Доказательство. Рассмотрим на [a,b] вспомогательную функцию
F(x)= f (x)− f (a)− |
f (b)− f (a) |
(x − a). |
|
||
|
b − a |
|
Легко проверить, что эта функция удовлетворяет всем условиям теоремы Ролля. Действительно, она непрерывна на [a,b], поскольку является раз-
ностью между непрерывной функцией f (x ) и линейной функцией. F(x) на интервале (a,b) имеет (конечную) производную, равную
′ |
′ |
f (b)− f (a) |
|
|
|
||
F (x )= |
f (x )− b − a . |
||
На концах отрезка [a,b] функция F(x) принимает одинаковые значения:
F(a)= F(b)= 0.
|
Итак, для функции F(x) |
на [a,b] выполнены все три условия теоремы |
|||||||
Ролля. Применяя эту теорему к функции F(x), |
заключаем, что существует та- |
||||||||
кая точка |
′ |
то есть |
′ |
f (b)− f (a) |
= 0, откуда получаем |
||||
b − a |
|
||||||||
c (a,b), что F (c)= 0, |
f (c)− |
||||||||
|
f (b)− f (a) |
′ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
b − a |
= f (c). |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
Равенство (18) называют формулой Лагранжа. Иногда ее записывают в |
||||||||
виде |
|
|
|
|
|
|
|||
|
|
|
f (b)− f (a) |
′ |
|
|
|
|
|
|
|
|
= f (c) (b − a), где a < c < b. |
|
|||||
Рассмотрим геометрическую иллюстрацию теоремы Лагранжа (рис.7).
166
