
mat_analiz
.pdf
вверх, а справа от точки x 0 y′′ > 0 и график функции обращен выпуклостью вниз
(рис.20).
y
0 |
x |
Рис. 20
План решения задач на определение интервалов выпуклости графика функции и нахождение точек перегиба.
1.Найти область определения функции.
2.Найти вторую производную функции.
3.Найти точки, где f ′′(x )= 0 или f ′′(x ) не существует. 4.Определить знак f ′′(x ) слева и справа от каждой из этих точек.
5.По достаточному условию выпуклости и достаточному условию точек перегиба определить характер выпуклости и сделать вывод о наличии точек перегиба.
Пример 50. Найти интервалы выпуклости и точки перегиба графика функ-
ции: |
|
|
|
|
а) y = x 4 − 6x 2 − 6x +1; |
б) y = 3 х + 2 ; |
в) y = |
1 |
. |
|
||||
|
|
|
х3 |
|
Решение. а) |
y = x 4 − 6x 2 −6x +1. |
|
|
|
1.Область определения ( − ∞; + ∞ ).
2. |
y′ = 4x 3 −12x − 6 , y′′ =12x 2 −12 . |
3. |
y′′ = 0 при 12x 2 −12 = 0 , то есть 12(x 2 −1) = 0 , x1 = −1 ; x 2 =1. |
4. |
Определим знак y′′ на каждом интервале (−∞; −1) , (−1; 1), (1; + ∞). |
187
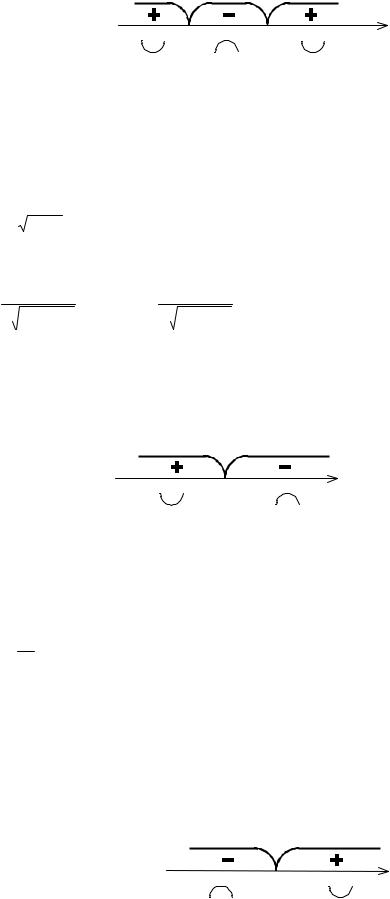
–1 |
1 |
x |
y(−1)= 2 , y(1)= −10 .
5.(−1; 2) и (1; −10) - точки перегиба графика функции, которая обращена выпук-
лостью вверх на промежутке (−1; 1) и выпуклостью вниз на промежутках (−∞; −1) и
(1; + ∞).
б) y = 3 х + 2 .
1.Область определения ( − ∞; + ∞ ).
2. |
y′ = |
1 |
; |
y′′ = − |
2 |
. |
|
33 (х + 2)2 |
93 (х + 2)5 |
||||||
|
|
|
|
|
|||
3. |
y′′ ≠ 0 , y′′ не существует при |
x = −2 (но данная функция определена при |
|||||
x= −2 ).
4.Определим знак y′′ слева и справа от точки x = −2 .
–2 x
y(− 2)= 0 .
5. Точка (− 2;0) – точка перегиба графика функции, обращенной выпуклостью вниз на промежутке (− ∞;−2) и выпуклостью вверх на промежутке(− 2;+∞).
в) y = x13 .
1.Область определения(− ∞;0)U(0;+∞).
2. |
3 |
; |
|
12 |
. |
|
y′ = − |
|
y′′ = |
|
|||
x 4 |
x5 |
|||||
3. |
y′′ ≠ 0 , y′′не существует при x = 0 (при x = 0 функция не определена). |
|||||
4.Определим знак y′′ слева и справа от точки x = 0 .
0 x
188
5. График функции обращен выпуклостью вверх при x < 0 и выпуклостью вниз приx > 0 . Точки перегиба нет.
Задания для самостоятельной работы
Найти интервалы выпуклости и точки перегиба графиков функций:
1. |
y = x3 − 6x2 +12x + 4 ; |
3. |
y = |
x3 |
|
|
; |
5. y = (x2 +1)ex . |
x2 + |
12 |
|
||||||
|
|
|
|
|
|
|
||
2. |
y = (x +1)4 ; |
4. |
y = x2 ln x ; |
|
|
|||
|
Ответы: 1. график |
функции |
обращен |
выпуклостью вверх при |
||||
x (− ∞; 2) и выпуклостью вниз при x (2; + ∞), точка перегиба (2;12). |
||||||||
2. точек перегиба нет, график обращен выпуклостью вниз на всей области определения.
3. график обращен выпуклостью вниз при |
x (− ∞; − 6)и (0; 6), |
выпуклостью |
|||||||||||||||||||
вверх при x (− 6; 0)и (6; + ∞), точки перегиба |
|
|
|
|
|
|
9 |
; (0;0) ; |
|
|
|
|
9 |
||||||||
|
− 6; − |
|
|
|
6; |
|
. |
||||||||||||||
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||
4. график функции обращен выпуклостью вверх при x |
|
|
− |
3 |
|
|
|||||||||||||||
|
|
||||||||||||||||||||
0; e |
2 |
|
и выпукло- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
3 |
|
|
|
|
− |
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
стью вниз при x e |
2 ; |
+ ∞ , точка перегиба |
e |
|
2 ; − |
|
|
e−3 . |
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. график обращен выпуклостью вниз при x (− ∞; −3)и (−1; + ∞), выпуклостью
|
|
|
10 |
|
|
2 |
|||
вверх при |
x (−3; −1), точки перегиба |
−3; |
|
|
, |
−1; |
|
. |
|
e3 |
e |
||||||||
|
|
|
|
|
|
|
|||
3. Асимптоты графика функции
При исследовании поведения функции y = f (x) при x → −∞ и при
x → +∞ , или вблизи точек разрыва, удобным оказывается рассмотрение асимптот графика функции.
Определение. Прямая называется асимптотой графика функции y = f (x), если расстояние d от точек графика до этой прямой стремится к ну-
лю при неограниченном удалении этих точек по графику функции в бесконечность.
189
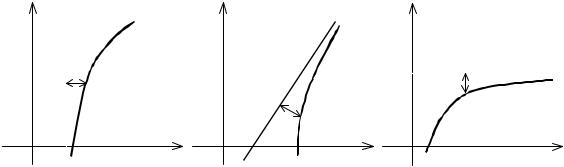
Различают три вида асимптот: вертикальные, наклонные и горизонтальные.
y |
|
|
x=x0 |
|
y |
|
|
y |
|
|
|
|
|
y=f(x) |
y=kx+b |
|
b N |
y=b |
|
|
|
|
d |
|
|
|
|||
|
|
|
|
|
y=f(x) |
||||
|
N |
|
M |
|
N |
d |
y=f(x) |
||
|
|
|
|
|
|||||
|
|
|
|
|
d |
M |
|
M |
|
|
|
|
|
|
|
|
|
||
0 |
x0 |
|
a) |
|
x 0 |
|
x 0 |
x |
|
|
|
|
|||||||
|
|
|
|
б) |
|
|
в) |
|
|
Рис. 21
На рис. 21 (а) изображена вертикальная асимптота, (б) – наклонная, (в) – вертикальная.
1. Вертикальная асимптота.
Пусть функция y = f (x) определена в некоторой окрестности точки x0 ,
кроме самой точки x0 .
Определение. |
Прямая |
x = x0 |
называется вертикальной асимптотой |
|||||||||||||
графика функции |
y = f (x), если хотя |
бы один из |
пределов |
|
lim f (x ) или |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x →x 0+0 |
||
lim f (x ) равен + ∞ или − ∞. Значит, (см. рис. 21 (а)) при x → x0 |
точки графика |
|||||||||||||||
x →x 0−0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функции М(x; f (x)) будут близки к точкам прямой |
x = x0 , т.е. |
расстояние |
||||||||||||||
d = MN стремится к нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 51. Рассмотрим асимптоты графика функции y = |
1 |
|
. Область |
|||||||||||||
|
x + 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
определения функции (− ∞; − 2)U(− 2; + ∞), т.е. функция |
y = |
|
1 |
|
не определена |
|||||||||||
x |
+ 2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при x = −2 и |
lim |
1 |
|
= +∞ и |
lim |
1 |
|
= −∞ . Значит, прямая x = −2 является |
||||||||
|
|
|
2 |
|||||||||||||
|
x →−2+0 x + 2 |
|
x →−2−0 x + |
|
|
|
|
|
|
|
|
|
||||
вертикальной асимптотой графика данной функции. |
|
|
|
|
|
|
|
|
||||||||
Замечание 24. Из определения вертикальной асимптоты следует, что |
||||||||||||||||
прямая x = x0 |
является асимптотой графика функции |
y = f (x) тогда и только |
||||||||||||||
тогда, когда функция в точке x0 имеет разрыв II рода. Следовательно, чтобы
190
отыскать вертикальные асимптоты, нужно найти все точки, где функция y = f (x) имеет бесконечный разрыв.
2. Наклонная асимптота.
Рассмотрим функцию y = f (x), определенную для сколь угодно боль-
шого положительного значения аргумента, т.е. при x → +∞. (Аналогично можно рассмотреть функцию, определенную для сколь угодно малого отрицательного аргумента, то есть при x → −∞ ).
Определение. Прямая называется наклонной асимптотой
графика функции y = f (x) при x → +∞, если функцию можно представить в виде f (x)= kx + b +α(x) , где α(x) - бесконечно малое при x → +∞, т.е.
lim α(x)= 0 .
x→+∞
Теорема 18. Для того, чтобы график функции y = f (x) имел при x → +∞
наклонную асимптоту y = kx + b , необходимо и достаточно, чтобы существо-
вали конечные пределы:
lim |
f (x) |
= k , |
lim (f (x)− kx)= b . |
||
x |
|
||||
x→+∞ |
|
x→+∞ |
|||
Доказательство. 1. Необходимость. Пусть график функции y = f (x) |
|||||
имеет наклонную асимптоту y = kx + b |
при x → +∞ , т.е. имеет место равенство |
|||||||||||||||
f (x)= kx + b +α(x) , где α(x) |
- бесконечно малое при x → +∞ . Тогда |
|||||||||||||||
|
f (x ) |
|
kx + b +α(x ) |
kx |
|
|
b |
|
α(x ) |
|
|
|
|
|||
lim |
|
|
= lim |
|
|
= lim |
|
+ |
|
|
+ |
|
= k ; |
|
|
|
x |
x |
x |
|
x |
x |
|
|
|
||||||||
x →+∞ |
x →+∞ |
x →+∞ |
|
|
|
|
|
|
|
|||||||
lim (f (x )− kx )= lim (kx + b +α(x )− kx )= lim (b +α(x ))= b . |
|
|||||||||||||||
x →+∞ |
|
|
|
x →+∞ |
|
|
|
x →+∞ |
|
|
|
|
||||
2. Достаточность. Пусть существуют пределы lim |
f (x) |
= k и |
lim (f (x)− kx)= b . |
|||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x→+∞ |
x |
x→+∞ |
|
Тогда |
lim (f (x)− kx)−b = lim (f (x)− kx −b)= 0 , |
т.е. |
f (x)= kx + b +α(x) , где |
|||||||||||||
|
|
|
x→+∞ |
|
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
lim α(x)= 0 . Значит, прямая y = kx + b является наклонной асимптотой графика
x→+∞
функции y = f (x) при x → +∞ . Теорема доказана.
Замечание 25. Аналогично определяется наклонная асимптота и доказывается теорема для случая, когда x → −∞ .
191

Замечание 26. Существование двух конечных пределов |
lim |
|
f (x) |
и |
||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
x→+∞ |
|
x |
|
|
|
||
lim (f (x)− kx) (аналогично при |
x → −∞ ) является обязательным условием для |
|||||||||||||||
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
существования наклонной асимптоты при x → +∞ (при |
x → −∞ ). Например, |
|||||||||||||||
график |
функции |
y = |
x |
не |
имеет |
асимптот, т.к. |
k = lim |
x |
= 0 , |
|
но |
|||||
b = lim ( |
x − 0 x)= ∞ . |
|
|
|
|
|
|
x→+∞ x |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 27. Если существуют только два конечных предела |
lim |
f (x) |
||||||||||||||
|
x |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
→+∞ |
|
||||
и lim (f (x)− kx) или |
lim |
f (x) |
и lim (f (x)− kx), то график функции имеет только |
|||||||||||||
x |
|
|||||||||||||||
x→+∞ |
|
x→−∞ |
x→−∞ |
|
|
|
|
|
|
|
|
|
||||
правостороннюю или левостороннюю асимптоту. |
|
|
|
|
|
|
|
|
||||||||
Замечание 28. При |
исследовании расположения |
графика |
функции |
|||||||||||||
y = f (x) |
относительно |
асимптот, отдельно рассматриваются |
случаи |
при |
||||||||||||
x → +∞ |
и x → −∞ . |
В каждом случае можно определить знак |
разности |
|||||||||||||
f (x)− (kx + b). Если |
знак этой |
разности |
положителен, то график |
функции |
||||||||||||
y = f (x) расположен над асимптотой, а если знак отрицателен, то под асим-
птотой. Если же разность меняет знак в зависимости от определенного значения x , то асимптота пересекает график функции.
Пример 52. Найти наклонные асимптоты графика функции
y = |
x2 + 3x + 5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Найдём k = lim |
y |
= lim |
x2 |
+ 3x + 5 |
=1. |
|
|
|
|
|
|||||||||
|
|
x(x +1) |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x→+∞ x |
|
x→+∞ |
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
+ 3x + 5 |
|
|
|
x |
2 |
+ 3x + 5 − x |
2 |
− x |
|
2x + 5 |
|
||||
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||
Найдём b = lim (y − kx)= lim |
|
|
|
|
|
− x |
= |
lim |
|
|
|
|
|
|
= lim |
|
= 2 . |
|||
|
|
x +1 |
|
|
|
|
x +1 |
|
|
x +1 |
||||||||||
|
x→+∞ |
x→+∞ |
|
|
|
x→+∞ |
|
|
|
|
|
x→+∞ |
|
|||||||
Следовательно, при график функции имеет наклонную асимптотуy = x + 2 . Аналогично, при x → −∞ можно убедиться, что значение пара-
метров k и b принимают те же значения. Значит, при и при x → −∞ график функции имеет единственную наклонную асимптоту y = x + 2 .
Ответ: y = x + 2 .
192
3. Горизонтальные асимптоты.
Из предыдущего определения наклонной асимптоты при k = 0 имеем:
Определение. Прямая y = b называется горизонтальной асимптотой
графика функции y = f (x) при x → +∞ , если lim f (x)= b и аналогично горизон- |
||||||||
|
|
|
|
|
|
|
x→+∞ |
|
тальной асимптотой при x → −∞ , если |
lim |
f (x )= b . |
|
|||||
|
|
|
|
|
x →−∞ |
|
|
|
|
Пример |
53. |
Найти |
горизонтальные |
асимптоты |
графика функции |
||
f (x)= arctg x . |
|
|
|
|
|
|
|
|
|
Решение. |
Имеем |
lim arctg x = |
π |
и |
lim arctg x = − |
π . Значит, прямые |
|
|
|
|
|
x→+∞ |
2 |
|
x→−∞ |
2 |
y = π |
и y = − |
π являются соответственно правосторонней и левосторонней |
||||||
2 |
|
2 |
|
|
|
|
|
|
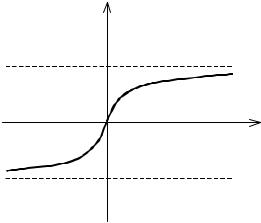
горизонтальными асимптотами графика функции f (x)= arctg x (см. рис.22).
y π |
|
y = |
π |
||||
|
2 |
|
|||||
|
2 |
|
|
||||
|
|
|
|
||||
|
|
|
y=arсtg x |
||||
|
|
|
|
|
|
|
x |
− |
π |
y = − |
|
π |
|||
2 |
|
|
|
||||
2 |
|
||||||
Рис. 22
Замечание 29. Практически для нахождении наклонной асимптоты при
k = 0 получаем горизонтальную асимптоту, если lim f (x) существует. Поэто-
x→±∞
му при нахождении асимптоты можно рассмотреть два случая: а) вертикальные и б) невертикальные (наклонные и горизонтальные) асимптоты.
Пример 54. Найти асимптоты графика функции y = 2x .
Решение: а) Вертикальных асимптот график функции не имеет, т.к. функция непрерывна на всей области определения (− ∞; + ∞).
б) Найдем невертикальные асимптоты:
193
k = lim |
f (x) |
= lim |
2x |
= lim |
(2x )′ |
= lim 2x ln 2 =+ ∞ . |
||
x |
|
x |
x′ |
|||||
x→+∞ |
x→+∞ |
x→+∞ |
x→+∞ |
|||||
Значит, при x → +∞ наклонной асимптоты не существует. Найдем наклонную асимптоту графика данной функции при x → −∞ :
k = lim |
f (x) |
= lim |
2x |
= lim |
2x ln 2 |
=0 . |
||
x |
|
x |
1 |
|||||
x→−∞ |
x→−∞ |
x→−∞ |
|
|||||
Это значит, что при x → −∞ график функции имеет только горизонтальную асимптоту:
b = lim |
f (x)= lim 2x |
= 0 . |
x→−∞ |
x→−∞ |
|
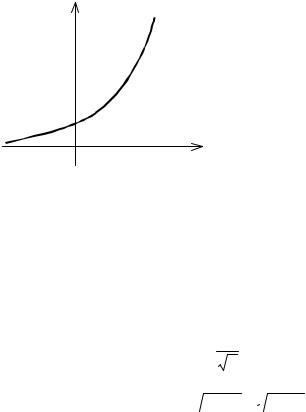
График данной функции имеет единственную горизонтальную асимптоту y = 0 при x → −∞ (см. рис.23).
y
y=2x
0 |
x |
|
Рис. 23 |
Задания для самостоятельной работы
Найти |
асимптоты следующих кривых: |
|
|
|||
1. |
y = |
x2 +1 |
. |
6. y = |
x2 |
. |
|
x2 − 4 |
|||||
|
|
x |
|
|
||
2. |
y = |
x2 |
|
. |
|
|
||
x +1 |
|
|
||||||
|
|
|
|
|
||||
3. |
y = |
|
x |
|
. |
|
|
|
x |
−1 |
|
|
|||||
|
|
|
|
|
||||
4. |
y = |
|
x2 |
. |
|
|||
2 |
− 2x |
|
||||||
|
|
|
|
|||||
5. |
y = |
|
5 |
|
|
. |
||
x |
2 − |
25 |
||||||
|
|
|
||||||
Ответы: 1. x = 0, y = x . 2. x = −1, y = x −1.
7.y = x − 1x .
8.y =  x2 +1 +
x2 +1 +  x2 −1 .
x2 −1 .
9.y = x ex .
10.y = ln(4 − x2 ).
6.x = ±2, y =1.
7.x = 0, y = x .
194

3. |
x =1, y =1 . |
|
|
8. |
y = ±2x . |
||
4. x =1, y = − |
1 |
x − |
1 |
. |
9. |
y = 0, x → −∞. |
|
|
2 |
||||||
|
2 |
|
|
|
|
||
5. |
x = ±5, y = 0 . |
|
|
10. x = ±2 . |
|||
4. Схема исследования функции и построения графиков.
Чтобы построить график функции y = f (x), проведем исследование
этой функции по следующей схеме:
1.Найти область определения функции.
2.Исследовать функцию на четность или нечетность, периодичность. При построении следует учесть, что если функция четная, то её график симметричен относительно оси y . Если функция нечетная, то её гра-
фик симметричен относительно начала координат.1
3.Найти точки пересечения графика функции с осями координат.
4.Найти асимптоты графика функции: а)вертикальные, б)невертикальные.
5.Найти интервалы монотонности и точки экстремумов.
6.Найти интервалы выпуклости вверх и вниз и точки перегиба графика функции.
7.Построить график функции, используя полученные результаты исследования.
Вслучае необходимости следует найти ещё несколько точек, принадлежащих графику функции.
Пример 55. Исследовать функции и построить их графики:
а) y = 4x3 − x4 . |
б) |
y = |
x4 −1 |
. |
в) y = x ex . |
|
|||||
|
|
|
x3 |
|
|
1 В случаях четной (нечетной) функции исследование можно проводить на половине области определения функции и затем достраивать график функции, используя свойство симметрии относительно оси ординат (начала координат). Если функция периодическая, то исследование можно проводить на промежутке длиной в один период и достраивать график влево и вправо, используя параллельный перенос.
195
Решение. а) y = 4x3 − x4 .
1.Область определения функции: (− ∞; + ∞).
2.Исследуем на четность и нечетность: y(− x)= 4(− x)3 − (− x)4 = −4x3 − x4 .
y(− x)≠ y(x), y(− x)≠ −y(x). Функция не является ни четной, ни нечетной.
3.Найдём точки пересечения с осями координат:
Сосью Oy : x = 0 , тогда y = 0 .
Сосью Ox : y = 0 , тогда 4x3 − x4 = 0, x3 (4 − x)= 0, x = 0, x = 4 .
Точки пересечения с осью Oy и Ox (0;0) и (4;0).
4.а) Вертикальных асимптот график функции не имеет, т.к. функция всюду непрерывна.
б) Найдем невертикальные асимптоты графика функции, имеющие общий вид y = kx + b :
k = lim |
y |
= lim |
4x3 − x4 |
= lim x2 (4 − x)= −∞. |
|
x |
|||
x→+∞ x |
x→+∞ |
x→+∞ |
||
Значит, при x → +∞ асимптоты (правосторонней) график функции не имеет. Аналогично при x → −∞ можно показать, что левосторонней асимптоты график функции также не имеет. Значит, невертикальных асимптот график функции не имеет.
5.Найдем интервалы монотонности и точки экстремума.
y′ =12x 2 − 4x 3 = 4x 2 (3 − x ).
y′ = 0 при x = 0 , x = 3 - критические точки. Исследуем знак производной слева и справа от каждой критической точки:
|
max |
|
0 |
3 |
x |
При x (− ∞;3) график функции возрастает, при x (3;+∞) убывает, при x = 3 функция имеет максимум и
y(3)= 27 .
6.Найдём интервалы выпуклости вверх и вниз, точки перегиба.
196
