mat_analiz

y′′ = 24x −12x2 =12x(2 − x).

y′′ = 0 при x = 0 и x = 2 .

Исследуем на знак y′′ слева и справа от x = 0 и x = 2 .

0 2 x

При x (− ∞;0) и (2;+∞) график функции обращен выпуклостью вверх,

при x (0; 2) выпуклостью вниз.

y(0)= 0; y(2)=16 .

(0;0) и (2;16) - точки перегиба графика функции.

7.Построим график функции (см. рис. 24):

y

27

16

Рис. 24

б) y = x4 −1 .

x3

1.Область определения функции: (− ∞;0)U(0; + ∞).

2.Исследуем на четность или нечетность:

симметричен относительно начала координат.

3.Найдем точки пересечения с осями координат. С осью Ox : y = 0 .

x4 −1 = 0 , x4 −1 = 0 , x = ±1. x3

197

(1;0) и (−1;0) - точки пересечения с осью Ox .

С осью Oy точек пересечения нет (x ≠ 0).

4.Найдём асимптоты графика функции:

Значит, при x → +∞ график функции имеет наклонную асимптоту y = x .

При x → −∞ параметры k и b имеют те же значения. Других асимптот график функции не имеет.

5.Найдём интервалы монотонности и экстремумы:

y′ ≠ 0 , критических точек нет, y′ > 0 при любом x из области определения функции ( x ≠ 0 ). Значит, график функции возрастает на всей области определения.

6.Найдём интервалы выпуклости:

y′′ ≠ 0, y′′< 0 при x>0 и y′′ > 0 при x<0.

График функции обращен выпуклостью вверх при х>0 и вниз при х<0.

7.Строим график функции: (рис.25)

198

y

y=x

Рис. 25

в) y = xe−x .

1.Область определения( − ∞;+∞ ).

2.Исследуем на четность или нечетность:

y(− x )= −xe x = −xe x ;

y(− x )≠ y(x ), y(− x )≠ −y(x ).

Функция не является ни четной, ни нечетной.

3. Найдем точки пересечения с осями координат. С осью Оу: x = 0 ; y(0)= 0 . С осью Ох также (0;0).

4.Найдем асимптоты:

а) вертикальных асимптот нет, так как функция непрерывна на всей области определения.

б) невертикальные:

Правосторонняя асимптота имеет вид: у=0. Для левосторонней асимптоты имеем

Значит, левосторонней асимптоты график функции не имеет.

5.Найдем интервалы монотонности и экстремумы функции:

y′ = x ′e−x + x (e−x )′ = e−x − xe −x = e−x (1 − x ) ,

199

y′ = 0 при e−x (1 − x ) = 0 ,

e−x ≠ 0 , x =1 - критическая точка.

Определим знак производной слева и справа от точки x =1 .

max

1 x

Значит, график функции возрастает при x (−∞;1) и убывает при

6.Определим интервалы выпуклости графика функции и точки перегиба:

y′′ = (e−x )′(1 − x )+ e−x (1 − x )′ = −e−x (1 − x ) − e−x = −e−x (1 − x +1) = −e−x (2 − x ) .

Определим знак y′′ слева и справа от точки x = 2 .

2 x

График функции обращен выпуклостью вверх при x (−∞;2) и выпук-

лостью вниз при x (2;+∞) . Точка перегиба графика данной функции ( 2; e22 )

7. Построим график функции, учитывая все полученные результаты исследования (рис.26). Дополнительная точка (−1; − e).

y

0,4

–2,7

Рис. 26

200

Задания для самостоятельной работы

2. Область определения (− ∞; + ∞), точки пересечения с осями координат (0; 0) и (4; 0), асимптот нет, ymax = y(3) = 5.4 , точки перегиба (0; 0) и (2; 3,2).

3. Область определения (− ∞; + ∞), точки пересечения с осями координат (0; 0)

и (1; 0), асимптот нет, ymin = y(14) = − 1627 , точки перегиба (1; 0) и (12 ; 1) .

201

8. Область определения (− ∞; − 2) (− 2; 2) (2; + ∞), точки пересечения с осями

9. Область определения (− ∞; 2) (2; + ∞), точки пересечения с осями коорди-

5. Наибольшее и наименьшее значение функции на отрезке.

На практике встречаются задачи, в которых требуется найти наибольшее или наименьшее значения функции на некотором промежутке.

Наибольшим значением (глобальным максимумом) функции называется самое большое, a наименьшим значением (глобальным минимумом) – самое меньшее из всех значений функции.

По теореме Вейерштрасса, если функция y = f (x ) определена и непре-

рывна на отрезке [a; b], то среди её значений на этом отрезке есть как наи-

большее, так и наименьшее.

Функция имеет только одно наибольшее значение и только одно наименьшее значение или может не иметь их совсем.

Например, функция y = sin x имеет наибольшее значение, равное 1 и

имеет наименьшее значение, равное -1; функция y = x 3 не имеет ни наиболь-

шего, ни наименьшего значений; функция y = x имеет наименьшее значе-

ние, равное нулю, но не имеет наибольшего значения; функция y =1 − x име-

ет наибольшее значение, равное 1, но не имеет наименьшего значения.

Если функция y = f (x ) дифференцируема на интервале (a; b), то наи-

большее и наименьшее значения функции на отрезке [a; b] могут достигаться

функцией:

202

1) либо во внутренней точке x 0 отрезка [a; b]. Эта точка x 0 являетcя

одной из критических точек, a значение функции y = f (x ) в этой точке явля-

ется максимумом (минимумом) функции;

2) либо в точках на концах отрезка [a; b].

y

Рис. 27

На рис. 27 наибольшее значение функции на конце отрезка x = b , а наименьшее – в точке минимума x 0 .

Нахождение наибольшего (наименьшего) значения непрерывной функции на отрезке [a; b] осуществляется по следующему плану:

1.Определить критические точки функции y = f (x ), принадлежащие ин-

тервалу (a; b).

2.Вычислить значение функции y = f (x ) в найденных критических точ-

ках и на концах отрезка [a; b].

3. Среди найденных значений функции выбрать наибольшее (наименьшее) значение.

Замечание 30. Если поставлена задача нахождения наибольшего или наименьшего значения функции y = f (x ) на отрезке [a; b], то, очевидно, что нет необходимости выяснять характер этих критических точек.

203

не имеет конечного значения) при x = 0 . Эти критические точки принадлежат заданному отрезку [-1;1].

На концах отрезка функция принимает значения f (−1) = 3; f (1) = −1.

3.Из найденных значений функции f (12) ; f (0) ; f (−1) ; f (1) наибольшим

204

f(- 1) = - 12 .

Задания для самостоятельной работы

Найти наибольшее и наименьшее значения функции на указанных отрезках.

205

6. Нахождение наибольшего или наименьшего значений в практических задачах.

Решение многих задач практики приводит к отысканию наибольшего или наименьшего значения некоторой функции, вытекающей из условия задачи.

Пример 57. Какими должны быть размеры прямоугольника с заданным периметром 72 м, чтобы его площадь была наибольшей?

Решение. Обозначим основание прямоугольника х, тогда его высота

отысканию наибольшего значения этой функции. Функция S (x ) дифферен-

цируема для любого x (0; 36), причем S ′(x )= 36 − 2x .

S ′(x )= 0 при 36 − 2x = 0 , то есть при x =18 и 18 (0; 36). Найдём вторую произ-

водную S ′′(x )= −2 < 0 .Значит, в точке x =18 функция S (x ) имеет максимум.

Значение функции в этой критической точке S (18)= 324 . На концах отрезка

[0; 36] имеем S (0)= 0 ; S (36)= 0 .

Итак, прямоугольник, имеющий заданный периметр 72 м, будет иметь наибольшую площадь 324 м2 , если его размеры будут 18 м и 18 м, то есть он будет иметь форму квадрата.

Ответ: 18 м, 18 м.

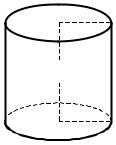
Пример 58. Консервная банка данного объема V имеет форму закрытого цилиндра. Какими должны быть её размеры (высота и радиус основания), чтобы на её изготовление пошло минимальное количество жести?

Решение. Пусть r радиус основания банки, h высота банки (рис.28).

r

h

Рис. 28

206