Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Красноярский государственный педагогический университет им. В.П. Астафьева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

mat_analiz

.pdf

Скачиваний:

163

Добавлен:

10.02.2015

Размер:

2.98 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 3615 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

функцию y = arcsin x

на интервале (−1, 1) . Она является обратной для функции

x = sin y, где

−

. На интервале

−

имеем: x ′y = cos y ≠ 0 . Со-

гласно правилу дифференцирования обратной функции получаем :

′

(arcsin x )

= cos y =

1 −sin 2 y

= 1 − x 2 .

Таким образом: (arcsin x )′ =

x (−1, 1).

1 − x 2

Аналогично, можно показать, что

(arccos x )′ =

, x (−1, 1);

1 − x 2

′

(arctgx )

x (− ∞, + ∞);

1 + x 2

′

(arcctgx )

= −

x (− ∞, + ∞).

1 + x 2

′

Отметим, однако, что формулы (arccos x )

= − 1 − x 2

и (arcctgx )

= −

1 + x 2

можно

также

получить,

используя

формулы (arcsin x )′ =

1 − x 2

′

(arctgx ) =

и равенства arccos x

= 2 − arcsin x,

arcctgx =

2 − arctgx .

1 + x 2

Замечание 8. Можно доказать, что если функция

y = f (x)

определена,

непрерывна, строго монотонна в некоторой окрестности точки

и в точке

имеет производную f ′(x 0 )= 0 , то обратная функция x = g(y)имеет в точке

= f (x0 )

бесконечную производную.

Задания для самостоятельной работы

1. Используя правило дифференцирования обратной функции, доказать формулы:

а)	(arccos x )′ =		1		, x (−1, 1);
			1 − x 2
	′		1
б)	(arctgx ) =			,	x (− ∞, + ∞);
		1 + x 2

137

′	1
в) (arcctgx ) = −			,	x (− ∞, + ∞).
		1 + x 2
2. Вывести	формулу			(loga x )′ =	1	loga e , воспользовавшись правилом

					x
дифференцирования обратной функции и формулой (ax )′ = ax ln a .

3. Получить формулу (ax )′ = ax ln a , применяя правило дифференциро-

вания обратной функции и формулу (loga x )′ =					1	loga e .

					x
4. Найти производную функции y = 5 x + 5 , используя правило диффе-
ренцирования обратной функции.
Ответ: 4. y	′			1
		=	55	(x + 5)4 .

§ 6. Правило дифференцирования сложной функции

Прежде всего, отметим особую значимость правила отыскания производной сложной функции. Умение практически применять это правило крайне важно потому, что при изучении различных процессов и явлений часто приходится исследовать именно сложные функции. Понятие сложной функции дано в главе I. Напомним это понятие. Пусть функция u = ϕ(x )определена на


множестве Χ , функция y = f (u)		определена на множестве U, причем множе-
ство значений функции u = ϕ(x )		содержится в области определения функции
y = f (u),	то есть, если x0 Χ , то ϕ(x 0 ) U . Тогда на множестве Χ определена
функция	y = f [ϕ(x)] которую называют суперпозицией функций y = f (u) и
u = ϕ(x ),	или сложной функцией, составленной из функций y = f (u) и u = ϕ(x ).

Для нее u - промежуточный аргумент (промежуточная переменная), x - независимый аргумент (независимая переменная). Например, сложными являют-

ся следующие функции: y = cos x2 (при этом y = cos u , u = x2 ); y = e x (при этом y = eu , u = x ); y = arcsin(2 − x) (при этом y = arcsin u, u = 2 − x ).

Теорема 3. Пусть y = f (u) и u = ϕ(x ) - заданные функции и пусть в не-

которой окрестности точки x0 определена сложная функция y = f [ϕ(x)]. Если

138

функция u = ϕ(x ) имеет производную в точке x0 , а функция y = f (u) имеет производную в точке u0 =ϕ(x 0 ), то сложная функция y = f [ϕ(x)] имеет произ-

водную в точке x0 , причем

y′(x 0 )= f ′(u0 ) ϕ′(x 0 ) .

(4)

Доказательство. Обозначим через Χ ту окрестность точки x0 , в ко-

торой определена сложная функция y = f [ϕ(x)]. Дадим аргументу x в точке

x0 приращение ∆x ≠ 0 , такое, чтобы точка x0	+ ∆x Χ . Тогда функция u = ϕ(x )
получит приращение ∆u , а, следовательно, и функция		y = f (u) получит при-
ращение ∆y , которое можно записать в виде
∆y = f ′(u0 ) ∆u +α(∆u) ∆u ,		(5)
где α(∆u)→ 0 при ∆u → 0 (см. §3).
Отметим, что функция α(∆u) не определена при ∆u = 0 . Но приращение
∆u зависит от выбранного ∆x ≠ 0 и может,	в частности, получиться равным
нулю. В связи с этим доопределим функцию	α(∆u) , полагая α(0)= 0 . В таком

случае равенство (5) остается верным и при ∆u = 0 . Разделим обе части равенства (5) на ∆x ≠ 0 . Получим

	∆y	= f ′(u0 ) ∆u	+α(∆u) ∆u .		(6)
	∆x	= f ′(u0 ) ∆u	+α(∆u) ∆u .		(6)
	∆x	∆x	∆x
Пусть теперь ∆x → 0 . По условию теоремы существует lim				∆u	=ϕ′(x 0 ). Кро-
			∆x →0	∆x
ме того, из дифференцируемости функции u = ϕ(x) в точке				x0 следует ее не-

прерывность в этой точке, а значит ∆u → 0 при ∆x → 0 . Но тогда α(∆u)→ 0.

Итак, при ∆x → 0 правая часть равенства (6) имеет предел, причем, учитывая, что f ′(u0 ) - постоянный множитель и используя теоремы о пределах,

находим:

lim	f ′(u0 )	∆u	+α(∆u)	∆u	= f ′(u0 ) ϕ′(x 0 ).
		∆x
∆x →0				∆x

139

А тогда существует предел и левой части равенства (6), то есть lim			∆y	и этот
		∆x→0	∆x
предел равен f ′(u0 ) ϕ′(x 0 ). Поскольку lim	∆y	= y′(x 0 ), то получаем:
предел равен f ′(u0 ) ϕ′(x 0 ). Поскольку lim		= y′(x 0 ), то получаем:
∆x →0	∆x
y′(x 0 )= f ′(u0 ) ϕ′(x 0 ).
Теорема доказана.
Сформулируем кратко правило дифференцирования сложной функции:
если y = f (u), а u = ϕ(x ), то производная сложной функции y(x)= f [ϕ(x)]				по не-
зависимой переменной x равна произведению производной функции				y по

промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной x .

Замечание 9. Используя другое обозначение производной и опуская значение аргумента, формулу (4) часто записывают в следующем виде:

dydx = dudy dudx .

Если с помощью нижнего индекса x или u указать, по какой переменной взята производная, то формула (4) примет вид:

y′x = yu′ u′x .

Пример 20. Найти производную функции y = tg(1 + x3 ).
Решение. С помощью промежуточного аргумента u
данную функцию так: y = tgu, где u =1 + x3 . Тогда yu′ =	1	,
	cos2 u

представим за- u′x = 3x 2 . Сле-

довательно, согласно правилу дифференцирования сложной функции имеем:

y′x = cos12 u 3x 2 .

Теперь, записывая 1 + x3 вместо u , получаем:


	′		3x 2
y	′	= cos2		(1 + x 3 ).
y		= cos2		(1 + x 3 ).

Пример 21. Найти производную функции y = 3 x5 − 4 .

Решение. В данном примере имеем: y = 3 u , где u = x5 − 4 .

140

Поскольку yu′ = 1	, u′x	= 5x 4 , то y′x = 1 5x 4 , откуда, подставляя
33 u 2		33 u 2
x5 − 4 вместо u , получаем:
		5x 4
		y′ = 33 (x 5 − 4)2 .
В приведенном выше правиле рассмотрена сложная функция y = f [ϕ(x)],
составленная из двух функций:		y = f (u) и u = ϕ(x ). Здесь y зависит от x через

посредство одной промежуточной переменной u . Однако правило дифференцирования сложной функции распространяется и на случай суперпозиции любого конечного числа функций, то есть на случай любого конечного числа промежуточных переменных. Например, если сложная функция составлена

из трех функций y = f (u), u = ϕ(v), v =ψ (x), причем v =ψ (x)

дифференцируема в

точке x0 , а

u = ϕ(v) и y = f (u) дифференцируемы соответственно в точках

v0 =ψ(x 0 ) и u0 = ϕ(v0 ), то

y′(x 0 )= f ′(u0 ) ϕ′(v0 ) ψ′(x 0 ).

Опуская значение аргумента и используя другие обозначения произ-

водных, последнее равенство можно переписать в виде:

или

y′x = yu′ uv′

v′x .

Пример 22. Найти производную функции y = sin 3 ( x −1).

Решение. С помощью промежуточных переменных u и v представим

заданную функцию так: y = u3 ,

где

u = sin v , а v =

x −1.

Поэтому, учитывая,

что yu′ = 3u 2 ,

uv′ = cos v, v′x =

и y′x

= yu′ uv′ v′x , получаем:

y′x = 3u 2 cos v

1 .

Подставляя вместо u и v их выражения через x , окончательно имеем:

′

3 sin 2 ( x −1) cos( x −1)

= 3sin

( x −1) cos(

x −1) 2 x

= 2

141

В приведенных выше примерах для разъяснения практического применения правила дифференцирования сложной функции промежуточные переменные обозначали буквами u и v и с помощью них записывали сложную функцию в виде цепочки более простых зависимостей. Однако таким образом желательно поступать лишь первое время, затем указанное представление сложной функции лучше выполнять устно.

Покажем на примерах, как можно рассуждать в этом случае.

Пример 23. Найти производную функции y = cos 2x +3.

Решение. Заданная функция есть косинус некоторого выражения. Мысленно принимая это выражение за промежуточную переменную, то есть за u , а затем, используя правило дифференцирования сложной функции, получаем:

y′ = −sin 2x + 3 ( 2x +3)′.

Для отыскания ( 2x +3)′ за промежуточную переменную мысленно обо-

значаем подкоренное выражение. Применяя правило дифференцирования сложной функции, можем записать:

( 2x + 3)′ =	1	(2x + 3)′ =	1	2 =	1 .
	2 2x + 3		2 2x + 3		2x + 3

Таким образом, окончательно имеем:

y′ = − sin 2x + 3 . 2x + 3

Приведенные рассуждения можно оформить следующим образом:

	′				′	1	′
y	′	= −sin 2x + 3 (		2x + 3) = −sin		2x + 3 2 2x + 3 (2x + 3) =
y		= −sin 2x + 3 (		2x + 3) = −sin		2x + 3 2 2x + 3 (2x + 3) =
= −sin 2x + 3				1	2 = − sin	2x + 3 .
			2	2x + 3		2x + 3

Пример 24. Найти производную функции y = ln5arctg x 3 .

Решение. Рассуждая аналогично тому, как это сделано при решении примера 23, получаем:

142

′

= 5 ln

arctg x

(ln arctg x

)

= 5 ln

arctg x

(arctg x

) =

arctg x 3

5 ln 4 arctg x 3

(x 3 )′

5 ln 4 arctg x 3

3x 2

15x 2 ln 4 arctg x 3 .

arctg x 3

1 + x 6

arctg x 3

1 + x 6

(1 + x 6 ) arctg x 3

С приобретением навыка дифференцирования сложной функции записи можно еще более сократить, выполняя все промежуточные рассуждения мысленно и записывая только их результат.

Пример 25. Найти производную функции y =

ctg e3

x .

Решение. Имеем

3 x

e3 x

′

−

= −

2 ctg e

sin 2 e

33 x 2

ctg e

sin 2 e

63 x 2

Замечание 10. Для отыскания производных некоторых функций можно воспользоваться методом логарифмического дифференцирования. Коротко суть его состоит в том, что заданную функцию, прежде всего, логарифмируем, после чего приравниваем результаты дифференцирования обеих частей полученного равенства и выражаем искомую производную.

Пример 26. Найти производную функции y =	(x 4 +1)5 7x 2 +8 .
	cos2 x

Решение. Прежде всего, логарифмируем заданную функцию. Полу-

чаем

ln y = 5 ln(x 4 +1)+ 12 ln(7x 2 +8)−ln cos2 x.

Теперь дифференцируем по x обе части полученного равенства, учитывая при этом, что в левой части равенства имеем сложную функцию от x . В результате приходим к выражению:

y′ =

20x 3

+ 2 tg x ,

x 4 +1

7x 2 +8

откуда получаем:

20x 3

y′

= y

+ 2 tg x ,

следовательно,

143

′

+1) 7x

20x

+ 2 tg x .

cos

Очевидно, что производную рассматриваемой в примере 26 функции можно найти, опираясь только на правила дифференцирования и не применяя метод логарифмического дифференцирования. Но использованный в примере метод логарифмического дифференцирования предпочтителен, поскольку быстрее приводит к цели.

Пример 27. Найти производную функции y = (x 2 + 4)sin x .

Решение. Логарифмируя заданную функцию, получаем равенство ln y = sin x ln(x 2 + 4).

Дифференцируем по x обе части этого равенства. Имеем:

y′ = cos x ln(x

+ 4)+

2x sin x

x 2 + 4

+ 4)+

2x sin x

Следовательно,

y′ = y cos x ln(x

, откуда получаем:

x 2 + 4

	2	sin x		2		2x sin x
y′ = (x		+ 4)	cos x ln(x		+ 4)+			.
y′ = (x		+ 4)	cos x ln(x		+ 4)+	x 2		.
						x 2	+ 4

Рассмотренная в последнем примере функция является показательностепенной. Используя метод логарифмического дифференцирования, легко устанавливается следующее правило дифференцирования показательно-

степенной функции: пусть y = uv , причем u = u(x )

и v = v(x ) –

дифференци-

руемые в данной точке функции и u(x )> 0 . Тогда

(uv )′ = uv ln u v′+ v uv−1 u′.

Задания для самостоятельной работы

1. Найти производные следующих функций:

а) y = (x 2 −4)5 ;

б) y = 3 2 −5x ;

в) y =

;

г) y = 1

;

(7x − 2)3

4 1− x 4

д) y = cos x ;

е) y = e−x

; ж) y =tg3x;

з) y = ln

и) y = arcctg 3 + x 4 ;

2 1

−

;

144

к)

y = arctg

1 + 1+e2x ;

л) y = e5x sin π x ;

м) x = ln

; н) y = (x 2 +1)sin x .

t 2 + 4

2. Найти значения производных заданных функций в указанных точках.

а)

y = 16 + x2 , x0

= 3;

б)

y = esin 3 x ,

x 0 =

π ;

(1 −

2t ),

t0 = −

в)

S = t +

cos

;

г)

y = ln3 (1 + sin x)+ arctg 2 (1 + sin x),

= 0.

3. Доказать,

что для функции

y = tg

справедливо равенство

y′− x (y 2 +1)= 0.

Ответы:

1. а) y ′ = 10 x (x 2 − 4 )4 ;

г) y′	=			x 3
			(1 − x 4 ) 4 1 − x 4
ж) y	′			3tg 2 x	з)
		= cos2 x ;

;

y′ =

б)		y	′	= −					5
						33 (2 −

д)		y	′	= −		sin			x
							2		x

					x
	2 ln 1 −
					2
								;
		x − 2

;

	;	в)	y′ = −	84	;
)2				(7x − 2)4

е) y′ = −2x e −x 2 ;

и)	2x 3
и)	y′ = − (4 + x 4 ) 3 + x 4	;

к)

y′ =

e2x

л) y′ = e5x (5sin πx +π cosπ x );

м)

1 + e2x

− x 2 +1

;

x ′ =

t(t 2 + 4);

sin x

2x sin x

н)

y′ =

(x 2

+1)

cos x

ln(x 2 +1)+

x 2

2. а) 3

;

б) 0;

в) 0;

г)

π .

§7. Геометрический смысл производной. Механический смысл производной

1. Геометрический смысл производной

Понятие производной функции y = f (x) в заданной точке x0 имеет на-

глядную геометрическую интерпретацию. Это понятие связано с понятием касательной к графику заданной функции.

145

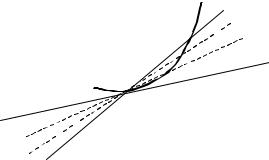
Прежде всего, поясним понятие касательной к кривой. Пусть L – плоская кривая и M 0 - точка на ней (см. рис. 2).

Рис. 2

Возьмем на этой кривой некоторую другую точку M . Проведем через точки M 0 и M прямую M 0 M . Эту прямую называют секущей. Пусть точка

M 0 остается неподвижной, а точка M движется по кривой L, неограниченно приближаясь к точке M 0 . Тогда секущая будет вращаться вокруг точки M 0 .

При этом может оказаться, что секущая M 0 M будет стремиться занять в пре-

деле положение вполне определенной проходящей через точку M 0 прямой.

Обозначим эту прямую через M 0T . В этом случае говорят, что кривая L в

точке M 0 имеет касательную M 0T .
Таким образом, касательной к кривой L в точке M 0	называют прямую
M 0T , ккоторойстремится секущая M 0 M , когдаточка M стремится кточке M 0 .
(Здесь имеется в виду, что угол между прямой M 0T	и секущей M 0 M

стремится к нулю при стремлении к нулю расстояния между точками M 0 и

M .)

Заметим, что касательная существует не всегда.

Перейдем теперь к рассмотрению геометрического смысла производ-

ной. Пусть функция y = f (x )	определена на	интервале (a, b) и в точке
x 0 (a, b) имеет производную	f ′(x 0 ). Покажем,	что существует касательная к

графику этой функции в точке M 0 (x 0 ; f (x 0 )), причем угловой коэффициент этой касательной равен f ′(x 0 ). Действительно, дадим аргументу x в точке x0

приращение ∆x ≠ 0 , такое, чтобы x 0 + ∆x (a, b). Тогда функция y = f (x ) полу-

146

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 3615 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.03.2016530.94 Кб91latina.doc
#
24.04.20192.01 Mб52Leblanc_Lupin_M.doc
#
20.04.2019154.82 Кб76Lektsii_po_gos_upravleniyu_i_politike.docx
#
20.09.2019390.14 Кб248lexicologie.doc
#
10.02.20154.22 Mб643Lysikova_O_V_Muzei_mira_Uchebnoe_posobie_-_M.pdf
#
10.02.20152.98 Mб163mat_analiz.pdf
#
25.09.20191.02 Mб53mat_logika.doc
#
10.02.2015273.41 Кб64METODIChESKIE_REKOMENDATsII_Yudenko.doc
#
14.11.2019274.43 Кб46METODIChESKIE_REKOMENDATsII_Yudenko.doc
#
23.08.201959.08 Кб4metodich_ukaz_k_kurs_rabotam_osn_biznesa.docx
#
10.02.201562.65 Кб22metodika_obuchenia_istorii.docx