mat_analiz

r = 3 2Vπ имеет минимум.

При исследовании функции S (r) на концах её области определения

207

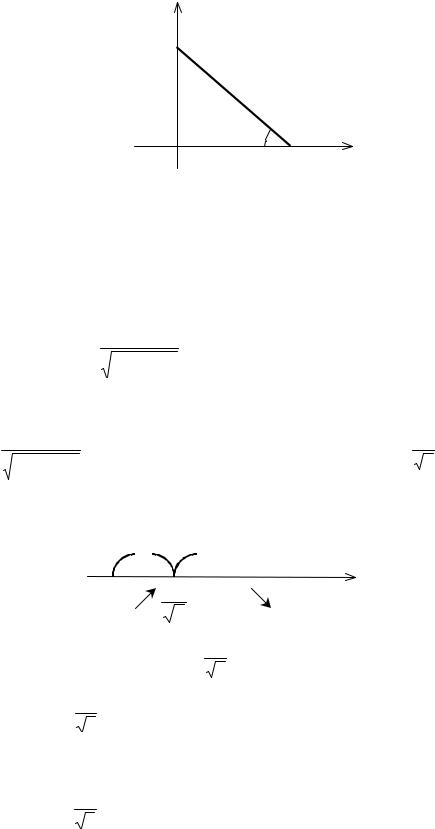
Пример 59. Пусть электрическая лампа перемещается по вертикали ОВ (оси Оу). На плоскости, перпендикулярной ОВ, возьмем точку А (на оси Ох). На какой высоте надо повесить лампу, чтобы в точке А была максимальная освещенность? (рис.29)

y

B

Значит, при h = a2 функция имеет максимум. При исследовании функции на

концах её области определения имеем: lim J (h) = 0; lim J (h) = 0 .

h→0+ h→+∞

Значит, при h = a2 функция принимает наибольшее значение.

208

Ответ. h = a2 .

Задания для самостоятельной работы

1.Решеткой длиной 120 м нужно огородить прилегающую к дому прямо-

угольную площадку наибольшей площади. Определить размеры прямоугольной площадки.

2.Дан прямоугольный лист жести со сторонами 20 см и 32 см. Требуется

изготовить открытую сверху коробку с дном в форме прямоугольника, вырезая по углам квадраты и загибая края так, чтобы объем коробки был наибольшим. Найти длину стороны вырезаемого квадрата.

3.Реакционный аппарат имеет форму открытого кругового цилиндра. При данном объеме цилиндра V, каковы должны быть радиус основания и высота цилиндра, чтобы площадь его поверхности была наименьшей?

4.Требуется изготовить воронку в форме конуса с образующей, равной 20 см. Какова должна быть высота воронки, чтобы ее объем был наиболь-

шим?

5.Материальная точка совершает прямолинейное движение по закону

s(t )= 5t + 2t 2 − 23 t 3 , где s - перемещение в метрах, t - время в секундах. В какой

момент времени t скорость движения точки будет наибольшей, и какова величина этой скорости?

6. В питательную среду вносят популяцию из 1000 бактерий. Численность популяции p(t) изменяется по закону p(t )=1000 + 1001000+tt2 , где t выражается в

часах. Найти максимальный размер этой популяции.

7. Реакция организма на введенное лекарство может выражаться в различных физиологических показателях: изменении кровяного давления, температуры тела, пульса. Степень реакции зависит от введенной дозы лекарства. Пусть х обозначает дозу введенного лекарства, степень реакции у описы-

вается функцией y = x 2 (a − x ), где а – некоторая положительная постоянная.

При каком значении х реакция организма максимальна?

209

8.В результате опытов получено n различных значений x1 , x 2 ,K, x n , ис-

следуемой величины А. Приближенным значением А выбирают такое число х, чтобы сумма квадратов отклонений его от каждого из была наименьшей. Найти х, удовлетворяющее этому условию.

210

ГЛАВА III. НЕОПРЕДЕЛЕННЫЙ ИНЕТЕГРАЛ §1. Понятие первообразной и неопределенного интеграла

Одной из основных задач дифференциального исчисления является задача нахождения производной или дифференциала функции.

В интегральном исчислении решается обратная задача – отыскание функции по заданной ее производной или дифференциалу. К этой задаче приводят такие важные проблемы механики, как определение закона движения материальной точки, если известны ее скорость или ускорение.

стоянная, будет первообразной для данной функции.

Рассмотренный пример показывает, что если задача нахождения первообразной функции имеет хотя бы одно решение, то она имеет и бесконечное множество других решений, отличающихся от упомянутого на произвольное постоянное слагаемое.

Возникает вопрос: исчерпывается ли множество всех первообразных для данной функции f(x) выражением вида

211

где F(x) – одна из этих первообразных, или же у f(x) имеются первообразные, не получающиеся из (1) ни при каком значении С. Ответ дает следующая теорема.

Теорема 1. Выражение (1) охватывает все множество первообразных для функции f(x).

Определение 2. Совокупность всех первообразных для данной функции f(x) на некотором промежутке называется неопределенным интегралом от функции f(x) (на этом промежутке) и обозначается символом

∫ f (x )dx .

Знак ∫ называется знаком интеграла, функция f(x) – подынтегральной функцией, а выражение f(x)dx – подынтегральным выражением.

Если F(x) есть одна из первообразных для f(x), то в силу проведенных выше рассуждений имеем

∫ f (x )dx = F (x ) +C ,

где С – любая постоянная.

Возвращаясь к рассмотренному примеру, можем записать

∫x 3 dx = 14 x 4 +C .

Из определений 1 и 2 вытекает следующее правило: чтобы убедиться, справедливо ли равенство

∫ f (x )dx = Φ(x ) +C ,

где Φ(x ) – какая-нибудь функция, нужно показать, что

212

3)∫sindx2 x = −ctgx +C , так как (− ctgx )′ = sin12 x ;

4)∫sin 2xdx ≠ cos 2x +C , так как (cos 2x )′ ≠ sin 2x . (Чему равна эта производная?)

Нахождение первообразной для данной функции f (x ) называется интег-

рированием f (x ) .

И, наконец, рассмотрим вопрос: для каких функций существуют первообразные (а, значит, и неопределенный интеграл)? Ответ дает следующая теорема.

Теорема 2. Всякая непрерывная на данном промежутке функция f (x )

имеет на нем первообразную.

§ 2. Таблица интегралов

Из таблицы производных и определения неопределенного интеграла несложно получить таблицу интегралов:

1.∫0 dx = C ;

2.∫1dx = x +C ;

6.∫e x dx = e x +C ;

7.∫sin xdx = −cos x +C ;

8.∫cos xdx = sin x +C ;

9.∫cosdx2 x = tgx +C ;

10.∫sindx2 x = −ctgx +C ;

213

Данную таблицу дополним несколькими широко используемыми интегралами, которые, однако, не имеют аналогов среди формул таблицы производных:

13.∫tgxdx = −ln cos x +C ;

14.∫ctgxdx = ln sin x +C ;

15.∫a2 dx+ x 2 = 1a arctg xa +C ;

16.∫a2 dx− x 2 = 21a ln aa +− xx +C ;

Для проверки всех формул этой таблицы интегралов достаточно установить, что производная правой части равенства совпадает с подынтегральной функцией левой части.

Рассмотрим, например, формулу 4:

Для ее доказательства достаточно показать, что

Действительно, рассматривая два случая, имеем: а) если x > 0 , то x = x . Следовательно, получим

(ln x )′ = (ln x )′ = x1 ;

б) если x < 0 , то x = −x . Тогда

214

(ln x )′ = (ln(− x ))′ = −1x (−1)= x1 .

доказана.

В случае формулы 17 имеем

что и требовалось доказать.

Аналогичным образом можно убедиться в справедливости остальных формул таблицы интегралов.

§3. Основные свойства неопределенного интеграла

1)Дифференциал от неопределенного интеграла равен подынтегральному выражению, то есть

2)Интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:

Эти два свойства непосредственно вытекают из определения неопределенно-

го интеграла и означают, что знаки d и ∫ взаимно сокращаются (во втором случае к F (x ) нужно лишь прибавить произвольную постоянную С).

3)Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от слагаемых:

4)Постоянный множитель можно выносить за знак интеграла, то есть если

А=const, то

215

Замечание 1. Равенства (4) и (5) понимаются в том смысле, что разность между левой и правой частями каждого из них есть постоянная.

Заметим, что обычно при вычислении интегралов от отдельных слагаемых в правой части не вводят несколько произвольных постоянных, а, пользуясь тем, что алгебраическая сумма произвольных постоянных также является произвольной постоянной, приписывают одну постоянную в конце всех выкладок.

Пример 3. Вычислить ∫x 2x +2 3 dx .

Решение. Для того, чтобы свести данный интеграл к сумме табличных, прибавим к числителю и вычтем из него 3. Получим

Пример 4. Вычислить ∫cos(3x ) 3dx .

216