
mat_analiz
.pdf
|
|
y |
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
f(b)–f(a) |
|
|
|
|
|
|
|
|
|
|
|
b–a |
|
|
|
|
0 |
a |
c |
b |
x |
|
|
|
|
Рис. 7 |
|
|
Отношение |
f (b)− f (a) |
представляет собой угловой коэффициент секу- |
||||
|
b − a |
|
|
|
|
|
щей, проходящей через точки A(a; f (a)) и B(b; f (b)) графика функции y = f (x),
а f ′(c) - угловой коэффициент касательной, проведенной к графику этой же функции в точке (c; f (c)).
Теорема Лагранжа утверждает, что существует такая точка c (a,b), что касательная, проведенная к графику функции y = f (x) в точке (c; f (c)), парал-
лельна секущей AB .
Заметим, что таких точек может быть и несколько.
Теорема 7 (теорема Коши). Пусть функции f (x) и g(x) непрерывны на от-
резке [a,b], дифференцируемы на интервале (a,b), причем g′(x )≠ 0 в каждой точ-
ке x (a,b). Тогдасуществует точка c (a,b) такая, чтосправедливо равенство:
f (b)− f (a) |
|
f |
′ |
|
||
= |
(c) |
. |
(19) |
|||
g(b)− g(a) |
|
|
′ |
|||
|
g (c) |
|
||||
Доказательство. Сначала отметим, что обе части равенства (19) имеют определенный числовой смысл. Действительно, так как по условию теоремы g′(x )≠ 0 , то правая часть равенства имеет смысл. В левой части так-
же имеем: g(b)− g(a)≠ 0, поскольку в противном случае получили бы g(b)= g(a) и тогда функция g(x) удовлетворяла бы условиям теоремы Ролля, а
значит, ее производная в некоторой точке c (a, b) была бы равна нулю, а это не имеет места, так как по условию теоремы g′(x )≠ 0 для любого x (a,b).
167
Докажем теперь равенство (19). Рассмотрим вспомогательную функцию
|
F(x)= f (x)− f (a)− |
f (b)− f (a) |
(g(x)− g(a)). |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
g(b)− g(a) |
|
|
|
|
|
|
|
|
Легко проверить, что эта функция на [a,b] удовлетворяет условиям тео- |
|||||||||||||||
ремы Ролля. А поэтому найдется такая точка c (a, b), что |
|
′ |
|
Учитывая, |
|||||||||||
F (c)= 0. |
|||||||||||||||
что F ′(c)= f ′(c)− |
f (b)− f (a) |
g′(c), получаем: |
|
|
|
|
|
|
|
||||||
g(b)− g(a) |
|
|
|
|
|
|
|
|
|||||||
|
|
f |
(b)− f (a) |
|
|
|
f (b)− f (a) |
|
|
′ |
|
|
|||
|
′ |
′ |
|
|
= |
|
f (c) |
. |
|
||||||
|
|
|
|
|
|
|
|
|
|
′ |
|
||||
|
f (c)− |
g(b)− g(a) |
g (c)= 0 , или |
g(b)− g(a) |
|
|
|||||||||
|
|
|
|
|
|
|
g (c) |
|
|
||||||
Теорема доказана.
Равенство (19) называют формулой Коши.
Замечание 13. Теоремы Ролля, Лагранжа и Коши называют теоремами
осредних значениях.
§12. Применение производных для вычисления пределов функций
(правило Лопиталя)
Вопросы отыскания пределов функций уже рассматривались выше в главе I. Там же приводились различные приемы раскрытия неопределенностей. В данном параграфе речь пойдет об очень важном и практически удобном способе отыскания пределов отношений двух бесконечно малых или двух бесконечно больших функций при помощи производных. Этот способ называют правилом Лопиталя.
Прежде всего рассмотрим вопрос о раскрытии неопределенностей вида
00 . Справедлива следующая теорема.
Теорема 8. Пусть выполнены следующие условия:
1) функции f (x ) и g(x ) определены и дифференцируемы в некоторой окрест-
ности точки x0 , за исключением, может быть, самой точки x0 ;
2) |
lim |
f (x ) = lim g(x ) = 0; |
|
x →x0 |
x →x0 |
3) |
′ |
|
g (x ) ≠ 0 в окрестности точки x0 , за исключением, может быть, самой точ- |
||
ки x 0 ;
168

4. существует конечный или бесконечный, равный + ∞ или - ∞, предел
|
|
|
|
|
lim |
f ′(x ) |
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
x →x 0 |
g′(x ) |
||||
Тогда существует и предел |
|
lim |
|
f (x ) |
, причем справедливо равенство |
||||
|
g(x ) |
||||||||
|
x →x 0 |
|
|
|
|
||||
lim |
|
f (x ) |
= lim |
f ′(x ) |
. |
||||
|
|
|
|||||||
x →x 0 |
|
g(x ) |
|
x →x 0 |
g′(x ) |
||||
Приведенная теорема позволяет свести предел отношения двух бесконечно малых функций к пределу отношения их производных. Во многих случаях отыскание предела отношения производных оказывается проще.
Таким образом, теорема 8 устанавливает правило для раскрытия неопре-
деленностей вида 00 .
Если отношение производных снова окажется отношением бесконечно малых функций, удовлетворяющих условием теоремы 8, то теорему следует применить повторно. Иногда (при выполнении соответствующих условий) теорему 8 приходится применять несколько раз.
Рассмотрим примеры.
Пример 38. Пользуясь правилом Лопиталя, вычислить lim e x −e4 .
x →4 x −4
Решение. В данном примере f (x) = ex − e4 , g(x) = x − 4 . Эти функции удовлетворяют всем условиям теоремы 8. А поэтому заключаем, что предел при x → 4 отношения gf ((xx)) указанных функций существует и равен пределу
отношения их производных. Таким образом, получаем:
lim |
e x − e 4 |
= lim |
(e x −e 4 )′ |
= lim |
e x |
= e 4 . |
|
|
|
(x − 4)′ |
|
|
|
||||
x →4 x − 4 |
x →4 |
x →4 1 |
|
|
||||
В дальнейшем решения будем записывать кратко. |
|
|
||||||
Пример 39. Пользуясь правилом Лопиталя, найти lim |
14 |
+ x −4 . |
||||||
|
|
|
|
|
|
x →2 |
11 |
− x −3 |
169

Решение. Имеем неопределенность вида 00 . Применяя правило Лопи-
таля, получаем:
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
lim |
14 + x − 4 |
= lim |
( |
14 + x − 4)' |
= lim 2 |
14 + x |
= −lim |
11 − x = − |
3 . |
|
|||||
x→2 |
11 − x −3 |
x→2 |
( |
11 − x −3)' |
x→2 |
− |
|
1 |
|
x→2 |
14 + x |
4 |
|
||
|
|
|
|
|
|
2 |
11 − x |
|
|
|
|
|
|||
Пример 40. Пользуясь правилом Лопиталя, вычислить lim |
2 − e x |
−e −x |
. |
||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x →0 |
x 2 (x +1) |
||
Решение. Имеем неопределенность вида 00 . Применяем правило Ло-
питаля:
lim |
2 − e x − e −x |
= lim |
(2 − e x − e −x )′ |
= lim |
− e x + e −x . |
|
(x 2 (x +1))′ |
||||
x →0 |
x 2 (x +1) |
x →0 |
x →0 |
3x 2 + 2x |
Опять получили неопределенность вида 00 . Снова применяем правило Лопиталя:
lim |
e−x −e x |
= lim |
(e−x −e x )' |
= lim |
−e−x −e x |
= −1. |
|
3x 2 + 2x |
(3x 2 + 2x )' |
6x + 2 |
|||||
x →0 |
x →0 |
x →0 |
|
Итак,
lim |
2 −ex −e−x |
|
x 2 |
= −1. |
|
x →0 |
(x +1) |
|
Пример 41. Вычислить lim x cos x − x . x →0 x −sin x
Решение. Имеем неопределенность вида 00 . Применяя правило Лопи-
таля, получим:
lim x cos x − x |
|
x →0 |
x −sin x |
= lim |
cos x − x sin x −1 |
|
= lim − |
||
|
|||||
x →0 |
1 − cos x |
|
x →0 |
||
= lim |
−3cos x + x sin x |
= −3. |
|||
x →0 |
cos x |
|
|
||
2 sin x − x cos x = sin x
В данном примере правило Лопиталя было применено три раза.
170
Перейдем теперь к рассмотрению вопроса о раскрытии неопределенно-
стей вида ∞∞ . Справедлива следующая теорема, устанавливающая правило для раскрытия неопределенностей вида ∞∞ .
Теорема 9. Пусть выполнены следующие условия:
1)функции f (x) и g(x) определены и дифференцируемы в некоторой окре-
стности точки x0 , за исключением, может быть, самой точки x0 ;
2) |
lim |
f (x ) = lim g(x ) = ∞ ; |
|
|
|
|
|
|
|||
|
x →x 0 |
|
x →x 0 |
|
|
|
|
|
|
||
3) |
′ |
|
|
|
x0 , за исключением, может быть, самой точ- |
||||||
g (x ) ≠ 0 в окрестности точки |
|||||||||||
|
ки x0 ; |
|
|
|
|
|
|
||||
4) |
существует конечный или бесконечный, равный + ∞или − ∞, предел |
||||||||||
|
lim |
|
f ′(x ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x →x 0 |
g′(x ) |
|
|
|
|
|
|
|||
|
Тогда существует и предел |
lim |
|
f (x ) |
, причем справедливо равенство |
||||||
|
|
|
|||||||||
|
|
|
|
x →x 0 |
g(x ) |
|
|
||||
|
|
|
|
lim |
|
f (x ) |
= lim |
f '(x ) |
. |
||
|
|
|
|
|
g(x ) |
|
|||||
|
|
|
|
x →x 0 |
x →x 0 |
g'(x ) |
|||||
Пример 42. Вычислить lim |
ln x |
. |
|
|
|
|
|
||
x →0 ctgx |
|
|
||
Решение. Имеем неопределенность вида |
∞ |
. Используем правило Ло- |
||
|
|
|
∞ |
|
питаля:
|
ln x |
|
|
1 |
|
|
sin 2 x |
sin x |
|
|
||
|
|
|
|
x |
|
|
||||||
lim |
|
= lim |
|
|
= − lim |
|
= − lim |
|
sin x |
= −1 0 = 0 |
||
|
1 |
x |
x |
|||||||||
x→0 ctg x |
x→0 |
x→0 |
x→0 |
|
|
|||||||
|
|
|
− |
|
|
|
|
|
|
|
||
|
|
|
sin 2 x |
|
|
|
|
|
|
|||
Теорему 9, так же как и теорему 8, в некоторых случаях приходится применять несколько раз.
Замечание 14. Теоремы 8 и 9 распространяются и на тот случай, когда аргумент x стремится к бесконечности.
171
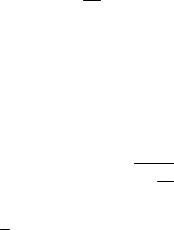
Пример 43. Вычислить lim |
x2 + 4x +1 |
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||
|
|
x→+∞ |
e |
5 x |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. В данном примере имеем неопределенность вида |
∞ |
. Приме- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
няя правило Лопиталя, получаем: |
|
|
|
|
|
|
|
|
|
|||||
lim |
x2 |
+ 4x +1 |
= lim |
2x + 4 |
= lim |
|
2 |
= 0 . |
|
|
||||
|
e5 x |
|
5 e5 x |
|
e5 x |
|
|
|||||||
x→+∞ |
|
|
x→+∞ |
x→+∞ 25 |
|
|
|
|||||||
Таким образом, |
lim |
x2 + 4x +1 |
= 0 . |
5 x |
x→+∞ e
Здесь правило Лопиталя применено два раза.
Как известно, при вычислении пределов функций кроме неопределенно-
стей вида 00 и ∞∞ встречаются также неопределенности других видов. Сущест-
вуют приемы, пользуясь которыми, неопределенности вида 0 ∞, ∞ − ∞, 1∞ ,
00 , ∞0 можно преобразовать к неопределенностям вида |
0 |
или |
∞ |
, которые |
||
|
|
|
0 |
|
∞ |
|
раскрываются по правилу Лопиталя. |
|
|
|
|
|
|
Рассмотрим это на примерах. |
|
|
|
|
|
|
Пример 44. Вычислить lim(1 − x2 ) tg |
πx |
. |
|
|
|
|
2 |
|
|
|
|
||
x→1 |
|
|
|
|
|
|
Решение. Выражение (1 − x2 ) tg π2x при x →1 представляет собой не-
определенность вида 0 ∞. Преобразуем его:
(1 − x2 ) tg |
πx |
= |
1 − x2 |
. |
||
2 |
|
|||||
|
|
ctg |
πx |
|||
|
|
|
2 |
|
|
|
Полученное после преобразования выражение 1− xπ2 при x →1 представляет ctg 2x
собой неопределенность вида 00 . Теперь можно применить правило Лопиталя.
Получаем:
172
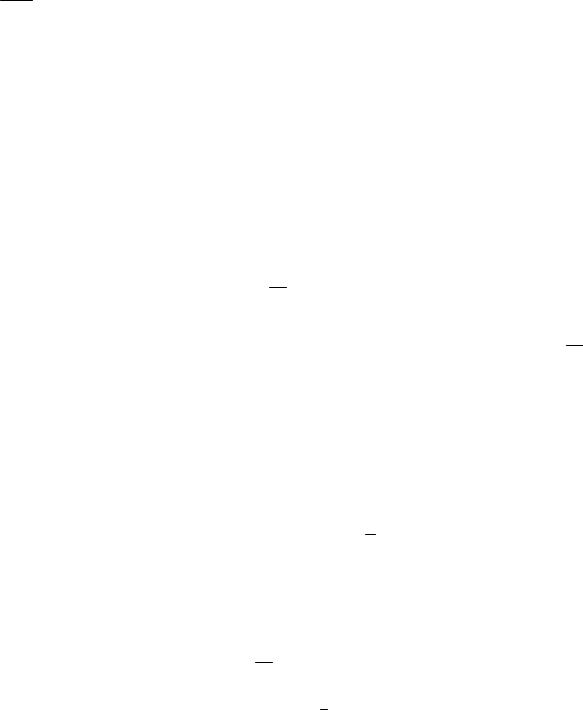
1
sin x
вида
lim(1 − x 2 ) tg πx |
= lim |
1 − x 2 |
|
= lim |
|
−2x |
|
|
= |
|
4 |
. |
|||
πx |
|
|
|
1 |
|
π |
|
||||||||
x →1 |
2 |
x →1 |
|
x →1 |
|
|
|
|
π |
||||||
|
|
|
|
ctg 2 |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
2 πx |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 45. Вычислить |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
−ctgx |
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x →0 sin x |
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Имеем неопределенность вида ∞ − ∞. Но поскольку
−ctgx = |
1 |
− |
cos x |
= |
1−cos x |
, то при x →0 приходим к неопределенности |
||
sin x |
sin x |
|
sin x |
|||||
|
|
|
|
|
|
|||
0 |
и, применяя правило Лопиталя, получим: |
|||||||
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
−cos x |
|
sin x |
= 0 . |
|
lim |
|
−ctgx |
= lim |
|
|
|
= lim |
|
|
|
|
|
sin x |
|
|||||
x →0 sin x |
|
x →0 |
|
|
x →0 cos x |
|
|||
Неопределенности вида 1∞ , ∞0 , 00 можно привести к неопределенностям вида 00 или ∞∞ с помощью предварительного логарифмирования.
Поясним это на двух примерах.
2
Пример 46. Вычислить lim x 1−x .
x →1
2
Решение. Имеем неопределенность вида 1∞ . Положим A = lim x 1−x . Ло-
x →1
гарифмируя обе части последнего равенства и используя непрерывность логарифмической функции, получаем:
2 |
2 |
|
|
2 |
|
ln x |
. |
||
ln A = ln lim x |
1−x |
= lim ln x |
1−x |
= lim |
|
ln x = 2 lim |
|||
1 |
− x |
|
|||||||
x →1 |
x →1 |
x →1 |
x →1 |
1− x |
|||||
Теперь имеем неопределенность вида 00 . Используя правило Лопиталя,
|
ln x |
|
|
1 |
|
|
|
получаем: 2 lim |
= 2 lim |
|
x |
|
= −2 . |
||
|
−1 |
||||||
x →11− x |
x →1 |
|
|||||
Итак, ln A = −2 , откуда A = e12
2 |
|
1 |
|
||
, то есть lim x |
1−x |
= |
. |
||
|
|||||
x →1 |
|
e2 |
|||
1 |
|
|
|
|
|
Пример 47. Вычислить lim (x + 3x ) x .
x →+∞
173

Решение. |
|
Имеем |
неопределенность |
|
вида |
|
∞0 . |
Положим |
|||||||||||||||||
1 |
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A = lim (x + 3x ) |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x →+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
1 |
|
|
|
ln(x + 3x ) |
|
|
|
1+3x ln 3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x +3x |
|
|
|
||||||||||
ln A = ln lim (x |
+ 3x ) |
|
= lim ln(x + 3x ) |
|
= lim |
|
= lim |
|
|
|
= |
||||||||||||||
x |
x |
|
|||||||||||||||||||||||
|
|
|
1 |
|
|||||||||||||||||||||
x →+∞ |
|
|
|
x →+∞ |
x →+∞ |
x |
|
x →+∞ |
|
|
|
||||||||||||||
|
= lim |
1+3x |
ln 3 |
= |
lim |
3x ln 2 3 |
= |
lim |
3x ln3 3 |
= ln 3. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x →+∞ |
|
x +3x |
x →+∞1+3x |
ln 3 |
x →+∞ 3x ln2 3 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Итак, ln A = ln 3 , откуда A = 3 , то есть lim (x + 3x ) |
|
= 3 . |
|
|
|
|
|
|
|||||||||||||||||
x |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x →+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь правило Лопиталя применено три раза. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Замечание 15. В заключение подчеркнем, что с помощью правила Лопиталя вычисляется предел отношения бесконечно малых или бесконечно больших функций в том случае, если существует предел отношения их производных. Если же предел отношения производных не существует, то отсюда еще не следует, что не существует и предел отношения самих функций.
Задания для самостоятельной работы
Применяя правило Лопиталя, вычислить следующие пределы:
1. lim ln(x −2) . |
5. lim |
x 2 + 7x −1 |
. |
|
|||
x →3 x 2 −9 |
x →+∞ |
e4x |
|
2. |
lim e3x −e−2x −5x . |
||
|
x →0 |
x 2 |
|
3. |
lim |
sin x − x cos x |
. |
|
|||
|
x →0 |
x 2 sin x |
|
4.lim ln x .
x→+∞ x 3
6. |
|
10 |
|
1 |
|
lim |
|
− |
|
. |
|
|
x −5 |
||||
|
x →5 x 2 −25 |
|
|
||
7.lim x ln sin 2x.
x→0
8.lim (sin x )tgx .
x→π2
Ответы: 1 . |
1 |
; |
|
2. 2,5; |
3. |
1 |
; |
4. 0; |
5. 0; |
|
|
6 |
|
|
|
|
3 |
|
|
|
|
6. |
− |
|
1 |
; |
7. 0; |
8. 1. |
|
|
|
|
|
|
|
|
|
||||||
|
10 |
|
|
|
|
|
|
|
||
174
§13. Исследование функций и построение графиков
1. Монотонность и экстремумы функции
Напомним, что функция у = f (х) непрерывная на промежутке Х, назы-
вается |
возрастающей (убывающей), если для любых |
x1, x2 X таких, что |
x1 < x2 , |
верно неравенство f (x1) ≤ f (x2 ) ( f (x1) ≥ f (x2 ) ). |
Если f (x1) < f (x 2 ) |
( f (x1) > f (x 2 ) ), то функцию называют строго возрастающей (строго убываю-
щей). Возрастающие и убывающие функции называются монотонными, а строго возрастающие и строго убывающие - строго монотонными. (Иногда используют иную терминологию: функции называют соответственно неубывающей, невозрастающей, возрастающей, убывающей).
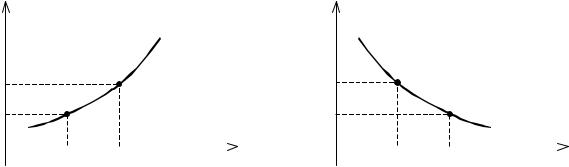
На рис.8 изображена возрастающая функция, на рис.9 – убывающая
функция. |
|
|
|
|
|
|
|
|
|
|
||
|
y |
|
|
y=f(x) |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f(x2) |
|
|
|
|
|
f(x1) |
|
|
y=f(x) |
|||
f(x1) |
|
|
|
|
|
f(x2) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x1 |
x2 |
x |
|
0 |
x1 |
x2 |
x |
||||
|
|
Рис. 8 |
|
|
|
|
|
Рис. 9 |
|
|
||
|
Теорема 10 (критерий постоянства функции). |
|
|
|
||||||||
|
Для того, |
чтобы функция f (x ) |
была постоянна на некотором проме- |
|||||||||
жутке Х, необходимо и достаточно, |
|
чтобы f (x ) |
была равна нулю во всех |
|||||||||
|
|
|
|
|
|
|
|
′ |
|
|
|
|
внутренних точках этого промежутка. |
|
|
|
|
||||||||
|
Доказательство. |
|
|
|
|
|
|
|
||||
|
1) Необходимость. Известно, |
|
что f (x )= const . |
Тогда |
очевидно, что |
|||||||
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
f (x ) = 0 . |
Достаточность. Дано, что f |
|
(x ) = 0 . Докажем, |
что f (x )= const . Возь- |
|||||||
2) |
|
|||||||||||
|
|
|
|
|
|
′ |
|
|
|
|
||
мем две произвольные точки x1, x2 X . Существует (по теореме Лагранжа) внутренняя точка c X такая, что f (x1 ) − f (x 2 ) = f ′(c)(x 2 − x1 ) . Так как f ′(с) = 0
175
по условию, то |
f (x1 ) − f (x 2 ) = 0 . Значит, |
каковы бы ни были x1, x2 верно, |
что |
||
f (x2 ) = f (x1 ) , т.е. |
f (x )= const . |
|
|
|
|
Теорема доказана. |
|
|
|
||
Теорема 11. (признак монотонности функции). |
|
|
|||
Если функция y = f (x ) непрерывна на [a; b], дифференцируема на (a; b) |
|||||
′ |
для любого x (a;b) , то функция возрастает на этом промежутке. |
||||
и f (x ) ≥ 0 |
|||||
′ |
≤ 0 для любого x (a;b) , то функция убывает на (a; b). |
|
|||
Если f (x ) |
|
||||
Доказательство. Возьмем две произвольные точки |
x1, x2 [a;b] |
та- |
|||
кие, что x1 < x2 . По теореме Лагранжа имеем f (x 2 ) − f (x1 ) = f |
′ |
где |
|||
(c)(x 2 − x1 ), |
|||||
c (a;b) .Значит |
по условию f (c) ≥ 0 . |
Имеем x2 − x1 > 0 , |
следовательно, |
||
|
|
′ |
|
|
|
f (x 2 ) − f (x1 ) ≥ 0 , |
то есть f (x1 ) ≤ f (x 2 ) , что означает возрастание функции на |
||||
(a; b). |
|
|
|
|
|
Аналогично доказывается убывание функции.
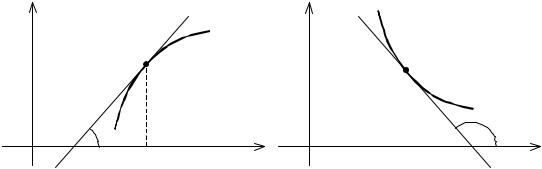
Геометрически утверждение теоремы означает, что в каждой точке графика возрастающей функции касательная либо образует острый угол с положительным направлением оси Ox, либо параллельна оси Ox, а в каждой точке графика убывающей функции касательная либо образует тупой угол с положительным направлением оси Ox, либо параллельна оси Ox. (рис.10 (а,б)).
y |
y=f(x) |
y |
|
|
|
|
|
y=f(x) |
|
α |
|
|
|
α |
|
|
|
|
|
|
0 |
x0 |
x |
0 |
x0 |
x |
|
a) |
Рис. 10 |
б) |
|
|
|
|
|
|
||
Например, |
для функции |
y = x3 |
имеем |
y′ = 3x 2 ≥ 0 при |
x R , значит |
функция y = x3 возрастающая функция. Касательная к графику данной функ-
ции в точке О (0; 0) параллельна оси Ox, а в остальных точках графика образует с осью Ox острый угол (см. рис.11).
176
