
mat_analiz
.pdf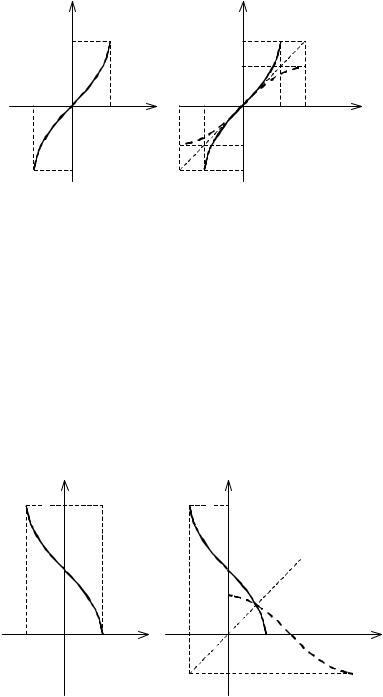
прямой y = x (см. рис. 29б).
а) |
|
б) |
πy y=arcsin x |
|
|
πy |
y=arcsin x |
|
|||
2 |
|
π |
2 |
y=sin x |
|
|
|
1 |
|||
–1 |
|
− 2 –1 |
|
|
|
|
|
0 1 π |
|
||
0 |
1 x |
|
x |
||
|
|
|
|
2 |
|
|
π |
|
|
–1π |
|
− |
2 |
y= x |
|
− 2 |
|
|
|
Рис. 29 |
|
|
|
б) Функция арккосинус |
y = arccos x . |
|
|
|
|
Арккосинусом числа x называют угол y выраженный в радианах, принадлежащий отрезку [0; π], косинус которого равен x , то есть cos y = x . Обла-
стью определения арккосинуса является отрезок [−1; 1], областью значений – отрезок [0; π]. Арккосинус является обратной функцией к косинусу, заданно-
му на отрезке [0; π] (см. рис. 30).
а) |
|
|
|
|
|
|
|
б) |
|
|
|
y=arccos x y |
|
|
|
|
|
y=arccos x y |
|
|
|||
|
|
π |
|
|
|
|
|
π |
|
|
|
|
π |
|
|
|
|
|
1 |
|
y=x |
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
–1 |
0 |
|
1 |
|
|
x |
–1 |
0 |
1 |
x |
|
|
|
|
|
|
|
|
|
–1 |
|
y=cos x |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Рис. 30 |
|
|
|
|
в) Функция арктангенс y = arctg x . |
|
|
|
||||||||
Арктангенсом числа |
x |
|
называют угол |
y |
выраженный в радианах, |
||||||
принадлежащий интервалу |
|
− |
π |
, |
π |
|
которого |
равен x , то есть |
|||
|
2 |
2 |
, тангенс |
||||||||
|
|
|
|
|
|
|
|
|
|
||
tg y = x .
Функция арктангенс определена для всех действительных чисел, множество
49
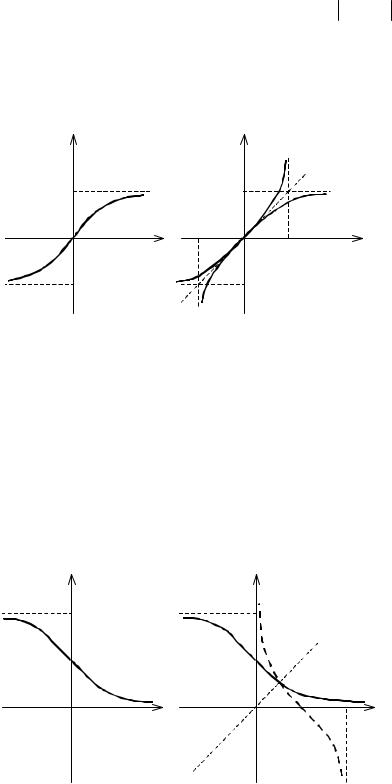
значений арктангенса Y = − π2 , π2 . Функция обладает свойством нечётности и возрастает с ростом аргумента, является ограниченной arctg x < π2 (см. рис. 31а). Арктангенс является обратной функцией к тангенсу, заданному на
промежутке |
|
− |
π |
, |
π |
|
(см. рис. 31б). |
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
а) |
|
|
y y=arctg x |
|
б) |
y y=tg x |
y=x |
||
|
|
|
|
|
|
|
|
π |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
− |
π |
2 |
y=arctg x |
|
|
|
|
|
|
|
|
|
2 |
|
||
0 |
x |
0 |
|
π |
x |
− |
π |
− |
π |
2 |
|
2 |
2 |
|
|
||
|
|
|
|
Рис. 31
г) Функция арккотангенс y = arcctg x . Арккотангенсом числа x назы-
вают угол y , выраженный в радианах и принадлежащий интервалу (0; π ), ко-
тангенс которого равен |
x , |
то есть |
ctg y = x . |
|
|
||
Область определения арккотангенса есть множество всех действитель- |
|||||||
ных чисел, множество значений Y = (0; π ). |
Арккотангенс является обратной |
||||||
функцией котангенсу, заданному на промежутке (0; π ) (см. рис. 32). |
|||||||
а) |
y |
|
|
б) |
y |
|
|
|
π |
|
|
|
π y=ctg x |
y=x |
|
|
|
|
|
|
|
|
|
|
π |
y=arcctg x |
|
π |
y=arcctg x |
||
|
2 |
|
|
|
2 |
||
|
|
|
|
|
|
||
|
|
0 |
x |
|
|
0 π |
π x |
|
|
|
|
|
|
2 |
|
Рис. 32
50

8. Сложные элементарные функции.
Примеры элементарных функций.
а) Многочлены n-ой степени представляют собой алгебраическую сумму константы и степенных функций с натуральными показателями степени от первой до n-ой включительно, умноженных на некоторые числовые коэффициенты. Многочлен n-ой степени имеет вид
y = axn + a |
n−1 |
xn−1 |
+ L + a x + a |
, |
||
|
|
|
1 |
0 |
|
|
где n N, a0 , a1 ,. . ., an - действительные числа, |
причем an ≠ 0 . Многочлены |
|||||
любой степени определены на множестве всех действительных чисел. Многочлены часто называют целыми рациональными функциями.
б) Дробно-рациональные функции. Функции, в которых над аргументом x производится сложение, вычитание, умножение, деление и возведение в натуральную степень, называют дробно-рациональными функциями.
Они представимы в виде отношения многочленов
|
y = |
a |
n |
xn + a |
n−1 |
xn−1 |
+ K + a x + a |
0 |
. |
|||
|
|
|
|
|
|
1 |
||||||
|
b xm +b |
|
xm−1 |
|
|
|||||||
|
|
|
+ K +b x +b |
|||||||||
|
|
m |
|
m−1 |
|
1 |
0 |
|
||||
Например: y = |
3x + 4 |
|
|
, y = |
|
2x |
. Дробно-рациональные функции |
|||||
x2 + x −1 |
|
x3 −1 |
||||||||||
|
|
|
|
|
|
|
||||||
определены для всех действительных чисел, которые не обращают знаменатель в ноль, то есть для всех чисел, кроме корней знаменателя.
в) Всякая функция, которая может быть явным образом задана с помощью формулы, содержащей лишь конечное число арифметических действий и суперпозиций элементарных функций, так же является элементарной
функцией. Например: y = sin log3 x, y = 4x2 + 2−x , y = x + tg x1 4 , y = 5e−3 x , 3x2 + 2 x
y = 4sin (12x −1).
51
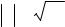
г) |
Функция абсолютная |
величина числа |
x : y = |
|
x |
|
x |
при |
x ≥ 0 |
, |
|
|
= |
|
|
||||||
|
|
|
|
|
|
|
− x |
при |
x < 0 |
|
|
|
|
|
|
|
|
||||
также является элементарной |
функцией. Ее |
можно представить в |
виде |
|||||||
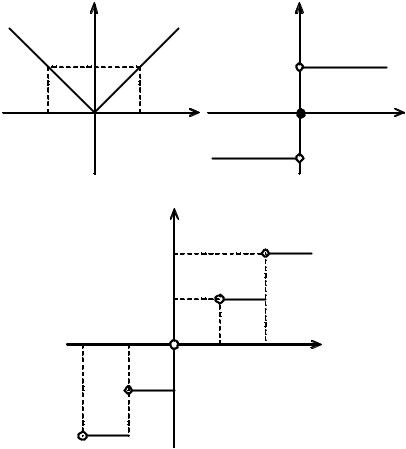
y = x = |
x2 . График этой функции приведен на рис. 33 а). |
|
|
|
||||||
Замечание. Класс элементарных функций наиболее изучен и чаще всего встречается в приложениях математики. Однако решение многих как теоретических так и практических задач математики приводят к рассмотрению функций не являющихся элементарными. Изучению таких функций посвящены специальные разделы математики. Приведем лишь два примера:
|
−1 |
при |
x < 0, |
|
знак числа x : |
|
0 |
при |
x = 0, |
y = sgn x = |
||||
|
|
1 |
при |
x > 0; |
|
|
|||
целая часть числа |
x : y = [ x ]. |
|
|
|
Словесное задание последней функции приведено в §2 данной главы. |
||||
На рис. 33 б) и в) |
приведены графики названных функций. |
|||
52
y |
y=|x| |
|
|
y |
y=sgn x |
|
|
|
|
||
1 |
|
|
|
1 |
|
–1 0 |
1 |
|
x |
0 |
x |
|
|
|
|
|
–1 |
а) |
|
|
б) |
||
|
|
y |
|
|
|
|
y=[x] |
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
–2 |
–1 |
0 |
1 |
2 |
x |
|
|
||||
|
|
|
–1 |
|
|
 –2
–2
в) Рис. 33
Задания для самостоятельной работы
В заданиях 1-11 постройте на одном рисунке графики указанных функций и сравните их:
1. |
y = x 2 , |
y = |
|
|
1 |
x 2 , |
y = 2x 2 ; |
||||||||||
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
y = x, |
|
y = x2 , |
|
|
y = x3 ; |
|
||||||||||
3. |
y = |
1 |
|
, |
y = − |
1 |
; |
|
|
|
|||||||
x |
x |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4. |
y = |
1 |
|
, |
y = |
1 |
|
|
, |
y = |
1 |
; |
|||||
x |
x2 |
x3 |
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
5. |
y = 2 x , |
y = 3x ; |
|
|
|
||||||||||||
6. |
y = 2 x , |
y = |
1 |
|
|
; |
|
|
|
||||||||
|
2 x |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7. |
y = log2 x, |
|
y = lg x ; |
|
|||||||||||||
53
8. |
y = log2 x, |
y = log 1 |
x; |
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
9. |
y = sin x, |
y = 3sin x, |
|
|
y = |
1 |
sin x; |
|
|
||||
|
|
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
y = sin x, |
y = sin 2x, |
|
|
y = sin |
1 |
x; |
|
|
||||
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
y = sin x, |
|
+ |
π |
|
, |
|
|
|
|
π |
||
y = sin x |
4 |
|
|
y = sin x − |
2 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
§4. Предел числовой последовательности. Числовые ряды
1. Понятие числовой последовательности
Пусть A некоторое счётное числовое множество и an - его элементы:
an A, n N .
Определение 8. Числовой последовательностью называют счётное множество действительных чисел, занумерованных всеми натуральными числами и расположенных в порядке возрастания номеров:
(1)
Число a1 - называют первым членом, a2 - вторым, … , an - n-ым (или общим)
членом последовательности, число n – номер члена последовательности. Все множество членов последовательности обозначается {an }. После-
довательность {an } является заданной, если указано правило, при помощи ко-
торого по номеру n можно найти значение любого члена последовательности, то есть если задана функция f (n):
an = f (n), n N K |
(2) |
Формулу (2) называют формулой общего члена последовательности. |
|
Таким образом, числовой последовательностью можно назвать множе- |
|
ство всех значений функции натурального аргумента: an = f (n), |
n N. |
Например: а) для арифметической прогрессии {an } общий член задается |
|
формулой |
|
an = a1 + d (n −1), n N K, |
(3) |
54
где a1 - первый член, d - разность прогрессии;
б) формула общего члена геометрической прогрессии имеет вид
a |
n |
= a qn−1 |
, n N K, |
(4) |
|
1 |
|
|
где a1 - первый член, q - знаменатель прогрессии.
Напомним, что сумма n первых членов: а) арифметической прогрессии
вычисляется по формуле Sn = |
|
a1 + an |
n или Sn = |
2a1 + d (n −1) |
|
n ; |
|||
2 |
|
|
|||||||
|
|
|
|
2 |
|
|
|||
б) геометрической прогрессии вычисляется по формуле |
|
||||||||
|
Sn = |
a1 (1 − q n ) |
, |
q ≠1 . |
|
||||
|
|
|
|||||||
|
|
|
1 − q |
|
|
|
|
||
Иногда последовательность задают, указывая несколько ее первых членов иправило, котороепозволяетвычислить общийчленчерезпредыдущиечлены.
Правило в этом случае называют рекуррентным соотношением, а способ задания последовательности рекуррентным.
55

Примером рекуррентного соотношения может служить формула для общего члена геометрической прогрессии. Действительно, ес-
ли известны значения a1 и |
q , то все остальные члены можно вычислить: |
a2 = a1 q, a3 = a2 q, K, an |
= an−1 q . Для арифметической прогрессии рекур- |
рентное соотношение иное, а именно: an = an−1 + d . |
|
Последовательность можно задать словесным описанием ее членов. В |
|
качестве примеров приведем следующие описания: |
|
а) геометрическая прогрессия есть последовательность чисел, в которой отношение любых последовательных чисел («последующее» деленное на «предыдущее») есть величина постоянная, называемая знаменателем прогрессии;
б) арифметическая прогрессия есть последовательность чисел, в которой разность любых двух последовательных чисел («последующее» минус «предыдущее») есть величина постоянная, называемая разностью прогрессии.
Члены последовательности {an } можно изобразить точками на число-
вой оси. На рис. 34 изображены пять членов последовательности an = |
1 |
, n N |
|||||||
n |
|||||||||
|
|
|
|
|
|
|
|
||
на оси Oy : |
|
|
|
|
|
|
|
||
|
|
a5 a4 a3 |
a2 |
a1 |
|
|
|
||
|
|
|
|
y |
|
|
|||
0 |
1 5 1 4 1 3 |
1 2 |
1 |
|
|
||||
|
|
|
|||||||
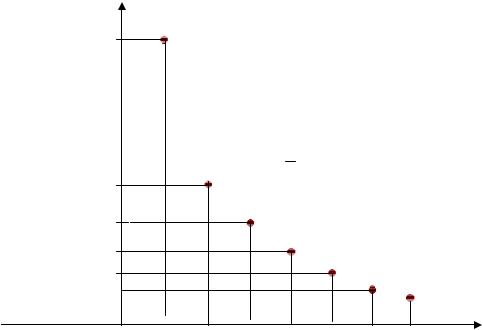
Рис. 34 На рис. 35 представлен другой способ изображения последовательно-
сти {an }, который основан на построении графика функции y = f (n), опреде-
ляющей общий член последовательности an = f (n), то есть на построении множества точек плоскости M n с координатами (n; an ).
55
y
1
y = an = 1n
1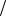 2
2
1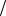 3
3
1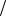 4
4
1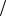 5
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||||||||
|
||||||||||||||||
Рис. 35
2. Монотонные и ограниченные последовательности
Определение 9 Последовательность {an } называют убывающей, если значения ее членов уменьшаются с увеличением их номеров:
a1 > a2 > a3 >K> an >K. |
|
Можно записать так: |
|
an > an+1 для всех n N |
(5) |
Последовательность, изображенная на рис. 34 и рис. 35, является убы- |
|
вающей. |
|
Определение 10. Последовательность {an } называют |
возрастающей, |
если значения ее членов возрастают с увеличением их номеров: |
|
a1 < a2 < a3 <K< an <K. |
|
Таким образом: |
|
an < an+1 для всех n N |
(6) |
Если в формулах (5) и (6) заменить строгое неравенство нестрогим, то последовательности называются невозрастающей и неубывающей соответственно. Последовательности неубывающие, убывающие, невозрастающие, возрастающие называют монотонными. Последовательность, все члены
56
которой принимают одно и то же значение называют постоянной последовательностью an = c, n N , где c некоторое число.
Определение 11. Последовательность {an } называют ограниченной,
если существует такое положительное число K , что для всех n N справед-
ливо неравенство |
|
|
an |
|
|
≤ K . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
В противном случае последовательность называют неограниченной. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Например, |
последовательность an = sin |
|
πn |
, n N является |
ограничен- |
||||||||||||||||||||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ной, так как |
|
|
an |
|
|
= |
|
sin |
πn |
|
|
|
|
≤1 для всех n N ; |
нашлось число K =1, |
такое что |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
an |
|
≤1, |
n N . |
|
|
Последовательность bn = n2 + |
, |
n N является неограничен- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ной, так как |
|
bn |
|
= |
n2 + |
|
|
|
> n2 |
для всех n , а |
|
n2 |
растет неограниченно с рос- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
том n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Замечание 1. |
|
|
|
|
Можно говорить о последовательности {an } ограничен- |
||||||||||||||||||||||||||||||||||||||||||||
ной снизу, если |
|
m ≤ an , |
|
n N , m - число, или ограниченной сверху, |
если |
|||||||||||||||||||||||||||||||||||||||||||||||
an ≤ M , |
n N , |
|
|
M -число. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
Замечание 2. |
|
|
|
|
Если |
|
последовательность {an } ограниченна, то она огра- |
||||||||||||||||||||||||||||||||||||||||||
ничена и сверху и снизу одновременно. Действительно, так как |
|
|
an |
|
|
≤ K , |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
то− K ≤ an ≤ K , |
|
|
n N и, следовательно m = −K , M = K . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
Замечание 3. Если |
|
|
последовательность |
{an } ограниченна и снизу и |
|||||||||||||||||||||||||||||||||||||||||||||
сверху |
одновременно, |
|
то |
она |
ограничена. |
|
Действительно, |
так |
как |
|||||||||||||||||||||||||||||||||||||||||||
m ≤ an ≤ M , n N , |
|
то справедливо |
неравенство: |
|
an |
|
≤ K , где K |
равно |
наи- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
большему из чисел |
|
m |
|
и |
|
M |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
Замечание 4. |
|
|
|
Если последовательность {an } ограничена ( |
|
an |
|
|
≤ K , n N ) |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
то все ее члены находятся на отрезке [− K ; K ] числовой оси. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
57
