
mat_analiz
.pdf
Определение 1. Абсолютной величиной, или модулем, действитель-
ного числа a называют неотрицательное число обозначаемое |
|
a |
|
и опреде- |
||||||||||
|
|
|||||||||||||
ляемое следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
= a, |
если |
a ≥ 0; |
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||
|
a |
|
= −a, |
если |
a < 0. |
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||
Ясно, что a ≥ 0, − a = a , |
a 2 = a2 , |
a2 |
= a . Если |
|
a |
|
= 0, |
|
то это экви- |
|||||
|
|
|
||||||||||||
валентно тому, что a = 0 . Для любых действительных чисел a и b справедливы следующие соотношения:
|
|
|
|
a b |
|
|
= |
|
a |
|
|
|
|
b |
|
; |
|
a |
|
|
= |
|
|
|
a |
|
|
, |
если b ≠ 0; |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
b |
|
|
|
b |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
a |
|
− |
|
b |
|
|
|
≤ |
|
a + b |
|
≤ |
|
a |
|
+ |
|
b |
|
; |
|
|
a |
|
− |
|
b |
|
≤ |
|
a −b |
|
≤ |
|
a |
|
+ |
|
b |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Определение 2. Подмножество X множества всех действительных чи- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
сел R |
называется ограниченным снизу, если существует действительное |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
число |
a |
(a R) такое, что оно не больше каждого числа x из X, то есть для |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
любого x |
(x X ) выполняется неравенство a ≤ x . Число a называют числом, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ограничивающим множество X снизу.
Множество, не являющиеся множеством ограниченным снизу, называют множеством неограниченным снизу. Термин «множество неограниченное снизу» означает, что каково бы ни было отрицательное, сколь угодно большое по абсолютной величине число a , в данном множестве обязательно найдется еще меньшее число x (x < a).
Если множество X ограничено снизу числом m , и число m принадлежит множеству X (m X ), то число m называют наименьшим или мини-
мальным числом множества X : m = min X . Если в множестве есть наимень-
шее число, то оно единственно.
Пример 3. а) множество чисел X = {1; 3; 8; 17} ограничено снизу числом
1, причем это число 1 является наименьшим;
11
б) множество X – множество всех неотрицательных чисел x (то есть чисел, удовлетворяющих неравенству x ≥ 0 ) тоже является ограниченным снизу и его наименьшим значением является число 0 ;
в) множество Y – множество всех положительных чисел y (то есть чи-
сел, удовлетворяющих неравенству y > 0 ) тоже является ограниченным снизу
числом 0 , но множество Y не имеет наименьшего, так как число 0 не принадлежит Y. При этом число 0 является наибольшим из всех чисел, ограничивающих множество Y снизу, а элементы y множества Y в силу свойств
плотности и непрерывности действительных чисел могут быть сколь угодно близки к числу 0 , оставаясь больше его;
г) множество D – множество всех отрицательных чисел неограниченно снизу, так как какое бы отрицательное число ни взять, найдется еще меньше число.
Определение 3. Подмножество X множества всех действительных чи-
сел R |
называется ограниченным сверху, |
если существует такое число |
|
b (b R), что оно не меньше каждого числа |
x |
(x X ), то есть для любого |
|
x X , |
выполняется неравенство x ≤ b. Число |
b |
называют числом ограничи- |
вающим множество X сверху.
Множество, не являющееся множеством ограниченным сверху, называют множеством неограниченным сверху. Термин «множество неограниченное сверху» означает, что каково бы ни было сколь угодно большое положительное число b , в данном множестве обязательно найдется еще большее число.
Если множество X ограничено сверху числом M и M X , то число M
называют наибольшим или максимальным числом множества X : M = max X . Если есть в множестве наибольшее число, то оно единствен-
ное.
Определение 4. Множество, ограниченное и снизу и сверху, называется ограниченным множеством.
12
Другими словами, множество X R ограничено, если существуют числа a , b (a R , b R) такие, что для каждого x X справедливо неравенство:
a ≤ x ≤ b.
Множество, не являющееся ограниченным, называют неограничен-
ным.
Пример 4. а) множество X = {1; 3; 8; 17} ограничено, так как для
всякого x X справедливо 1 ≤ x ≤17 , причем оно имеет и наименьшее значение m =1 и наибольшее M =17 ;
б) множество Y - множество положительных чисел, являясь ограниченным снизу, неограниченно сверху, (0 < y < +∞);
в) множество Z - множество всех целых чисел неограниченно как снизу, так и сверху (− ∞ < z < +∞).
Ясно, что чисел ограничивающих множество снизу (сверху) может быть много.
Определение 5. Наибольшее число среди всех чисел, ограничивающих снизу множество X R , называется нижней гранью (или инфимумом)
множества X и обозначается через inf X или infx {xX} (инфимум - от латин-
ского слова infimum – наименьший).
Например, для множества Y - множества всех положительных чисел нижней гранью является число 0, а для множества всех натуральных чисел N нижней гранью является число 1, оно является и наименьшим.
Определение 6. Наименьшее среди всех чисел, ограничивающих сверху множество (X R), называется верхней гранью (или супремумом) мно-
жества |
X и обозначается через sup X или |
sup{x} |
(супремум – от латинского |
|
|
x X |
|
слова supremum – наибольший).
Например, для множества всех отрицательных чисел число 0 является верхней гранью.
13
Если в множестве существует наименьшее (наибольшее) число, то оно является нижней (верхней) гранью этого множества. Приведем теорему без доказательства.
Теорема 1. Всякое ограниченное сверху непустое множество имеет верхнюю грань, а всякое ограниченное снизу непустое множество имеет нижнюю грань.
Множество всех действительных чисел x , удовлетворяющих двойному неравенству a < x < b , называют открытым промежутком или интервалом и обозначают (a ; b).
Множество всех действительных чисел x , удовлетворяющих двойному неравенству a ≤ x ≤ b , называют закрытым промежутком или отрезком и обозначают [a; b].
Пример 5. Примеры числовых множеств:
1. |
[a ; b) , если a ≤ x < b; |
2. |
(a ; b], если a < x ≤ b; |
||||
3. |
[a ; + ∞) , |
если |
a ≤ x < +∞; |
4. |
(a ; + ∞), |
если |
a < x < +∞; |
5. |
(−∞; b], |
если |
− ∞ < x ≤ b; |
6. |
(− ∞; b), |
если |
− ∞ < x < b; |
7. |
(− ∞; + ∞), если |
− ∞ < x < +∞; |
8. |
(− a ; a), |
если |
− a < x < a (a > 0); |
|
9. |
[− a ; a], |
если − a ≤ x ≤ a (a > 0); |
10. (a −ε ; a +ε ), |
если a −ε < x < a +ε (ε > 0). |
|||
Множества, приведенные под номерами 1 и 2, называют полуоткрытыми промежутками, множества под номерами 3, 4, 5, 6, 7 называют неограниченными промежутками, причем множество под номером 7 есть множество всех действительных чисел R.
Определение 7. Множество всех действительных чисел x , удовлетво-
ряющих двойному неравенству a −ε < x < a +ε , где ε > 0 , называют ε - окре-
стностью точки a. |
|
|
|
|
Этот факт можно записать следующим образом |
|
x − a |
|
< ε . Доказано, что |
|
|
|||
для любых двух неравных действительных чисел a и |
|
b существуют непере- |
||
секающиеся ε - окрестности. |
|
|
|
|
14
Числовое множество X называют симметричным относительно на-
чала координат, если этому множеству вместе с числом x принадлежит и ему противоположное число (− x), то есть, если x X , то и (− x) X .
Примерами таких множеств являются множества под номерами 7, 8, 9, а так же множество всех рациональных чисел Q и множество и т.д.
4. Комплексные числа
При решении алгебраических уравнений встречаются ситуации, когда уравнение не имеет корней в множестве действительных чисел. Например, квадратное уравнение не имеет действительных корней, если его дискриминант отрицательный.
Расширением понятия числа является понятие комплексного числа. Введено число i, которое считают решением квадратного уравнения
то есть считают справедливым равенство i2 +1 = 0 или i2 = −1. Это число i называют мнимой единицей.
Число b i , где b- действительное число, называют мнимым или чисто мнимым числом и считают его произведением действительного числа b и мнимой единицы i.
Комплексными числами называют выражения вида a +b i , где a и b -
действительные числа, i – мнимая единица.
Число a называют действительной (вещественной) частью, а число b –
мнимой |
частью |
комплексного числа z (используют обозначение: |
a = Re z; |
b = Jm z ). |
Если b = 0 , то комплексное число выражается только дей- |
ствительной частью и является действительным числом (a + 0i = a), таким об-
разом множество действительных чисел R является подмножеством множества комплексных чисел.
Числа
15
лексно сопряженными). Число, сопряженное числу |
z , принято обозначать |
|
. |
|||||||||||||||||||||||||||
z |
||||||||||||||||||||||||||||||
Два комплексных числа |
|
a1 + b1 i, a2 |
+ b2 i |
равны тогда и только тогда, |
когда |
|||||||||||||||||||||||||
равны |
их |
действительные |
|
и |
мнимые |
|
части |
одновременно, то |
есть |
|||||||||||||||||||||
a1 = a2 |
и b1 |
= b2 . Понятия отношений «больше» и «меньше» для комплексных |
||||||||||||||||||||||||||||
чисел не определены. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для комплексных чисел определены арифметические действия по сле- |
||||||||||||||||||||||||||||||
дующим правилам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) |
сложение и вычитание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
(a1 + b1i)± (a2 + b2i)= (a1 ± a2 )+ (b1 ± b2 ) i, |
|
|
|
|
|
||||||||||||||||||||
2) |
умножение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
(a1 + b1i) (a2 + b2i)= (a1a2 −b1b2 )+ (a1b2 + a2b1 ) i, |
|
|
|
|
|
|||||||||||||||||||||
3) |
деление |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
a1 + b1i |
= |
a1a2 + b1b2 |
+ |
|
a2b1 − a1b2 |
i, |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
a |
2 |
+ b |
i |
|
|
a2 + b |
2 |
|
|
|
a2 + b2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
2 |
|
2 |
2 |
|
|
|
|
|
|
|||||
причём деление на комплексное число 0 + 0 i не определено. |
|
|
|
|
|
|||||||||||||||||||||||||
Пример 6. Пусть |
z1 |
=1 + i , |
|
z2 = 2 −3i. Найти: z1 |
+ z2 , z1 z2 , |
z1 |
. |
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
z1 + z2 = (1 + i )+ (2 −3i )= (1 + 2)+ (1 −3) i = 3 − 2i ; |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
z1 − z2 = (1 + i )−(2 −3i )= (1 − 2)+ (1 + 3) i = −1 + 4i ; |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
z1 z2 = (1 + i ) (2 −3i )= (1 2 −1 (−3))+ (1 2 +1 (−3)) i = 5 −i ; |
|
|
|
||||||||||||||||||||||||
|
|
|
z1 |
= |
1 + i |
= |
|
|
−1 |
+ |
5 |
|
i = − |
1 |
|
+ |
5 |
i. |
|
|
|
|
|
|
|
|||||
|
|
|
|
2 −3i |
4 + 9 |
4 + |
9 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
z2 |
|
|
|
|
13 13 |
|
|
|
|
|
|
|
|
||||||||||||||
Определения действий над комплексными числами и правила этих действий установлены таким образом, чтобы они согласовывались с правилами действий над действительными числами. Так действия сложения и умножения комплексных чисел, как и действительных чисел, обладают свойствами:
1) переместительным (коммуникативным)
z1 + z2 = z2 + z1 , z1 z2 = z2 z1 ;
16
2) |
сочетательным (ассоциативным) |
|
|
|
|
|
||
|
(z1 + z2 )+ z3 = z1 + (z2 + z3 ), ( z1 z2 ) z3 = z1 (z2 z3 ); |
|||||||
3) |
распределительным (дистрибутивным) |
|
|
|
|
|||
|
|
z1 (z2 + z3 )= z1 z2 + z1 z3 . |
|
|
|
|
||
Модуль комплексного числа z = a + b i обозначают |
|
z |
|
или буквой r и |
||||
|
|
|||||||
определяют по формуле |
z = a2 + b2 , |
(r = |
z ). |
|
|
|
|
|
Например, если |
z = 2 +3i , то z |
= |
4 + 9 = 13, если |
z = −1 + 4i то |
||||
z = 1 +16 = 17. |
|
|
|
|
|
|
|
|
Легко убедиться, что модуль комплексного числа удовлетворяет таким же соотношением, какие были приведены для абсолютной величины действительного числа в пункте 3 данного параграфа.
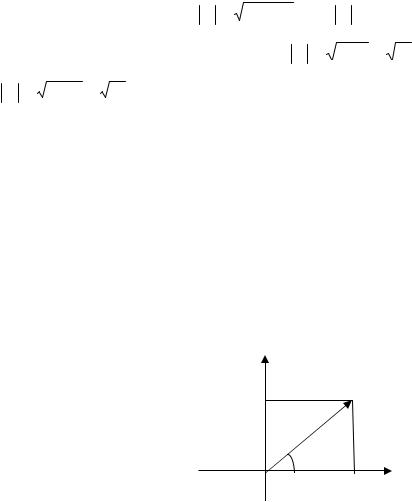
Между комплексными числами и точками плоскости можно установить взаимно однозначное соответствие и получить геометрическую интерпретацию комплексных чисел. Введем на плоскости прямоугольную декартовую систему координат.
Im
b |
M (a ; b) |
|||
|
|
|
|
|
OM |
|
|
||
|
ϕ |
|
|
|
O |
a |
Re |
||
|
Рис. 5 |
|
||
Каждому комплексному числу |
z = a + b i |
поставим в соответствие точ- |
||
ку плоскости M с абсциссой равной a и ординатой равной b : M (a ; b). Ясно,
что каждой точке координатной плоскости M (a ; b) соответствует комплекс-
ное число z = a + b i . Координатную плоскость в этом случае называют комплексной плоскостью. Ось абсцисс называют действительной осью Re, ось ординат – мнимой Im. (см. рис. 5)
17

Длина радиуса–вектора |
|
|
точки M (a ; b) равна модулю комплекс- |
|
OM |
||
ного числа z = a + b i ( z = |
a2 + b2 ). Угол ϕ между положительным на- |
||
правлением действительной оси и радиусом - вектором OM точки M (a ; b) на-
зывается аргументом комплексного числа z = a + b i .
Угол считается положительным, если его отсчет производится против движения часовой стрелки, и отрицательным в противном случае. Для числа равного нулю аргумент не определяется. Каждое комплексное число, не равное нулю, имеет бесчисленное количество аргументов. Любые два аргумента одного комплексного числа отличаются друг от друга слагаемым, кратным числу 2π . Наименьшее по абсолютной величине значение аргумента называ-
ется главным. Если известны модуль r |
и аргумент |
ϕ комплексного числа |
||||||||||||||||||||
z = a + b i , то a = r cosϕ , b = r sin ϕ ; |
tgϕ |
= |
b |
. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 7. |
а) |
Дано комплексное число |
z =1 −i . Найти его модуль и |
|||||||||||||||
главное значение аргумента. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
б) Даны модуль комплексного числа r = 4 и его аргумент ϕ = |
π . Найти |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
его действительную и мнимую части. Записать комплексное число. |
|
|
|
|||||||||||||||||||
|
|
|
|
Решение. |
|
а) |
Так |
как |
z =1 −i , |
то |
a =1, |
b = −1. |
|
Отсюда |
||||||||
r = |
|
z |
|
= |
12 + (−1)2 |
= |
2. |
Используя |
формулу |
tgϕ = |
b |
, |
получим |
уравнение |
||||||||
|
|
|||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
Его решение есть ϕ = −π |
+ kπ (k Z ), |
|
a |
|
M (1; −1) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
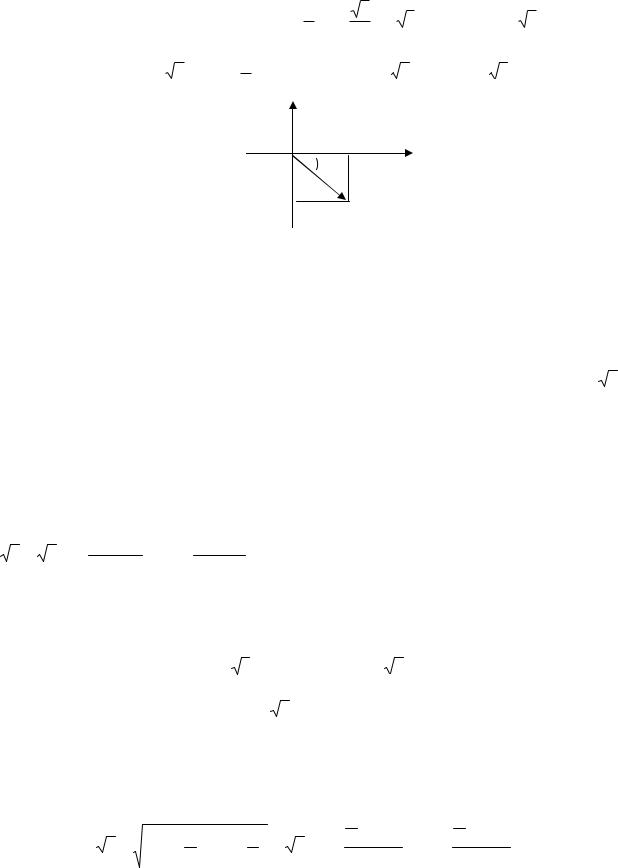
tgϕ = −1. |
но точка |
|
лежит |
в |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
четвертой четверти |
(см. рис. 6), |
поэтому аргумент |
ϕ = −π + 2kπ |
|
(k Z ), |
а |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
главное значение аргумента равно |
− |
π . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
По условию |
r = 4 , |
ϕ = |
π |
, следовательно, |
используя |
|
формулы |
||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
a = r cosϕ и b = r sin ϕ , получим
18
a = 4 cos |
π |
= 4 |
1 |
= 2, |
|
b = 4 sin |
π |
|
= 4 |
3 = 2 |
3, |
z = 2 + 2 3 i. |
|||
3 |
2 |
|
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
Ответ: |
а) |
r = |
2, |
ϕ = − |
π |
; |
б) |
a = 2, |
b = 2 |
3, |
z = 2 + 2 3 i. |
||||
|
|
|
|
|
|
|
4 |
|
Im |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
Re |
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
||
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
M (1;−1) |
|
|
Рис. 6
Если r - модуль комплексного числа z , а ϕ - главное значение его аргу-
мента, то можно записать z = r (cosϕ + i sin ϕ ).
Такую форму записи называют тригонометрической формой записи
комплексного числа. Используя эту форму записи, легко вычислить z n и n z для n N .
Возведение в n-ую степень комплексного числа производится по фор-
муле Муавра: |
z n |
= (r (cosϕ +i sin ϕ ))n |
= r n (cos nϕ + i sin nϕ). |
|
|
|
|||||||||||||||||||||||||
|
Извлечение |
корня |
|
|
n-ой |
степени |
|
|
|
|
|
производится |
по формуле |
||||||||||||||||||
|
|
|
|
ϕ + 2k |
π |
+ i sin |
ϕ + 2kπ |
|
где |
k=0,1,2, . . . , n-1. |
|
|
|
||||||||||||||||||
n z = n r cos |
|
n |
|
|
|
|
n |
|
, |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Последнее означает, что корень n-ой степени из комплексного числа |
||||||||||||||||||||||||||||||
имеет ровно n различных значений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Пример 8. |
|
Дано z =1 + |
3 i. |
Найти z3 |
|
|
и 3 |
|
z . |
|
|
|
||||||||||||||||||
|
Решение. |
Так как |
|
z =1 + |
3 i , |
то r = |
|
z |
|
= 2 и ϕ = |
π . Следовательно, |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
π |
|
|
|
π |
|
|
|
|
|
|
|
|
|
π |
|
|
π |
3 |
|
|
|
|
|||||||
|
+ i sin |
|
|
|
|
3 |
|
+i sin |
|
= 8(cosπ +i sinπ )= −8. |
|||||||||||||||||||||
z = 2 cos |
|
|
|
. Тогда z |
|
= 2 |
cos |
|
|
|
|
|
|
||||||||||||||||||
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
+ 2 kπ |
π |
|
|
||||||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
π |
|
|
|
|
|
|
|
|
+ 2 kπ |
||||||||
|
|
|
|
3 |
z = 3 |
+ i |
sin |
= 3 |
2 |
cos 3 |
|
|
|
|
|
+i sin 3 |
|
. |
|||||||||||||
|
|
|
|
2 cos |
3 |
3 |
|
|
3 |
|
3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагая k=0,1,2, получим три значения корня:
19
3 |
|
|
π |
+i sin |
π |
|
при k=0, |
|
|
|
3 |
2 |
|
7 |
π |
+i |
sin |
7 |
π |
|
при k=1, |
||||||
2 cos |
9 |
|
9 |
|
|
|
|
cos |
9 |
9 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 2 |
|
13 |
π |
+i sin |
13 |
π |
|
= 3 |
|
|
− |
5 |
|
|
|
|
|
− |
5 |
|
|
при k=2. |
|||||
cos |
|
|
|
|
|
2 cos |
|
π |
+ i sin |
|
π |
|
|||||||||||||||
|
|
9 |
|
|
|
|
9 |
|
|
|
|
|
|
9 |
|
|
|
|
9 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Задачи для самостоятельной работы
Ниже приведены ответы лишь на некоторые вопросы задач.
1. |
Пусть A = {4; 5; 7; 8}, B = {1; 4}, C = {0; 5; 7; 8}. Найти множества: |
|
A B, A C , B C , A ∩ B, A ∩C , A \ B, B \ A, A \ C , C \ A, B \ C , |
|
A ×C , B ×C , B × A, C × A, C ×B. |
2. |
Даны множества A = [1; 3], B = [2; 5], C = [5; 6]. Записать множества |
A B, A C, C B, A ∩ B, A ∩C, A \ B, B \ A, A \ C, C \ A, A B C и изо-
бразить их на числовой прямой.
3.Даны множества A = (−5; 7], B = [0; 3). Изобразить на числовой прямой множества A, B, A B, A ∩ B, A \ B.
4.Даны множества A = [−3; 0), B = [0; 4]. Записать множество A B и изо-
бразить его на числовой прямой.
5.Даны множества A = (2; 5), B = (3; 6). Изобразить на числовой прямой
|
множества A, B, A B, A ∩ B, A \ B, B \ A. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
Даны |
множества |
A = (−1; 1), B = (0; + ∞). Записать |
множества |
|
A B , |
|||||||||||||
|
A ∩ B , |
A \ B, B \ A и изобразить их на числовой прямой. |
|
|
|
|
|
|
|||||||||||
7. |
Даны множества |
A = [2; 3] и B = [1; 2]. |
Изобразить на |
координатной |
|||||||||||||||
|
плоскости множества A ×B и B × A . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8. |
Даны |
множества |
A = (1; + ∞), B = [1; 2). |
Изобразить |
на |
координатной |
|||||||||||||
|
плоскости множество A ×B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9. |
Изобразить на числовой прямой Ox множества, точки которых удов- |
||||||||||||||||||
|
летворяют следующим соотношениям: а) |
|
x |
|
≤ 5; б) |
|
|
x |
|
>1; в)1 < |
|
|
x |
|
≤ 5. |
||||
|
|
|
|
|
|
|
|||||||||||||
20
