Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Красноярский государственный педагогический университет им. В.П. Астафьева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

mat_analiz

.pdf

Скачиваний:

163

Добавлен:

10.02.2015

Размер:

2.98 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 3614 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Пример 9. Вычислить производную функции y = x .

		Решение.						Поскольку											1		, то по формуле (II) при α =				1	находим
																		x = x		2					1
																		x = x		2					2
																									2
		′		1	′		1		1	−1		1		−	1			1				′	1
		′			′		1			−1		1		−				1				′	1
y	′	= ( x )		2		=		x	2		=		x		2	=			. Итак,			( x ) =		.
y		= ( x )	= x			=	2	x			=	2	x			=	2		. Итак,			( x ) =		.
							2					2					2		x			2		x

Производные, полученные в примерах 8 и 9, часто встречаются на практике. Поэтому их полезно запомнить.

Пример 10.

Дана функция f (x)=

. Найти

′

(−1),

f (8).

Решение.

Учитывая,

что

= x−

применяем

формулу (II) при

−

−1

−

′

α = − 3 .

Имеем

(x )= − 3

= − 3 x

= −

3x 3 x 2

откуда при x = −1 и при

′

(−1)= −

x = 8 получаем соответственно

3 (−1) 3 (−1)2

= 3 ,

′

(8)= −

3 8 3 82

= − 48 . Таким образом,

(−1)= 3 , f

(8)= − 48 .

Задания для самостоятельной работы

1.Пользуясь таблицей производных основных элементарных функций, найти производные следующих функций:

а)

y = 5 ;

б)

y = x3 ;

в)

y =

; г) y = log2 x ; д)

y = 6

x ; е) y = ln 2 ;

ж)

y =

;

з) y = sin

; и)

y = 4 x3 ; к)

y = log1

x ;

л)

y = e5 .

Дана функция

f (x )= 4

f ′(0);

. Найти: а)

б) f

′

Дана функция

f (x)= 5

x . Найти f

(1)+ f

(−1).

4.При каких значениях аргумента производная функции y = 3 x равна 13 ?

127

Ответы: 1.

а) y′ = 0 ;

б)

y′ = 3x

;

в)

y′

; г)

y′ =

log2 e

или

y′ =

; д)

y′ =

; е)

y′ = 0 ; ж)

y′

= −

; з)

y′ = 0 ; и)

y′ =

;

x ln 2

6 6 x5

4 4 x

к) y′ =

log 1 e

или

y′ = −

;

л)

y′ = 0 .

x ln 3

2. а) 2 ln 2 ; б) 4 ln 2 . 3. −

. 4. x =1 и x = −1.

§3. О непрерывности дифференцируемой функции

Рассмотрим связь между дифференцируемостью функции в точке и ее непрерывностью в этой точке. Пусть функция y = f (x) в точке x0 дифферен-

цируема. Это означает, что существует конечный предел lim			∆ y	= f ′(x0 ). То-
		∆x→0	∆ x
гда согласно свойству пределов можем записать
∆y = f ′(x0 )+α (∆x), где	lim α(∆x)= 0 .
∆x	∆x→0
Отсюда получаем, что ∆y = f ′(x0 ) ∆x +α (∆x) ∆x и		lim ∆y = 0 .	Последнее ра-
		∆x→0
венство означает непрерывность функции y = f (x)		в точке x0 .

Таким образом, из дифференцируемости функции в точке следует непрерывность ее в этой точке. Отметим, что обратное утверждение неверно. Функция может быть непрерывной в точке, однако не иметь производной в этой точке.

§4. Правила дифференцирования суммы, разности, произведения и

частного дифференцируемых функций

Пусть u = u(x), v = v (x) - функции аргумента x .

Теорема 1. Если в точке x0 существуют производные функций u = u(x)

иv = v(x). , то в этой точке

1)существует и производная суммы u +v , при этом

(u + v)′(x0 )= u′(x0 )+ v′(x0 );

128

2) существует производная разности u − v, при этом

(u − v)′(x0 )= u′(x0 )− v′(x0 );

3) существует производная произведения u v, при этом

(u v)′(x0 )= u′(x0 ) v(x0 )+ u(x0 ) v′(x0 );

в частности, если c = const , то

(c u)′(x0 )= c u′(x0 );

4) при v(x0 )≠ 0 существует производная частного

, при этом

′

) v(x

)− u(x

′

)

v2 (x 0 )

Доказательство. Докажем 1).

Пусть y = u + v.

Дадим аргументу x

в точке x0 приращение ∆x ≠ 0 ( ∆x

выбирается про-

извольно, но так,

чтобы точка x0

+ ∆x

принадлежала области определения

рассматриваемых функций).

В результате этого функции

v получат

приращения соответственно

∆u = u (x0 + ∆x)−u (x0 )

∆v = v (x0

+ ∆x)−v (x0 ). А

следовательно, функция y = u + v также получит приращение ∆y ,

причем

∆y = [u (x0 + ∆x)+ v (x0 + ∆x)]−[u (x0 )+ v (x0 )]= [u (x0 + ∆x)−u (x0 )]+[v (x0 + ∆x)− v (x0 )]=

= ∆u + ∆v.

Таким образом,

∆y = ∆u + ∆v .

Разделив обе части последнего равенства на

∆x , получаем:

∆y =

∆u

∆v .

(1)

∆x

Пусть теперь ∆x стремится к нулю.

Поскольку по условию теоремы в

точке x0 существуют производные функций u и v , то существуют

lim

∆u = u′(x0 ) и

lim

∆v = v′(x0 ),

а, следовательно, правая часть равенства (1)

∆x→0

∆x

∆x→0

∆x

при ∆x → 0 имеет предел, причем

∆u

∆v

lim

∆u

+ lim

∆v

= u′(x0 )+ v′(x0 ).

lim

∆x

∆x→0

∆x→0 ∆x

∆x→0

129

А тогда существует предел и левой части равенства (1), то есть lim ∆y ,

∆x→0 ∆x

и этот предел равен u′(x0 )+ v′(x0 ). Таким образом, учитывая, что

lim ∆y = y′(x 0 ), получаем:

∆x →0 ∆x

y′(x0 )= u′(x0 )+ v′(x0 ), или (u + v)′ (x0 )= u′(x0 )+ v′(x0 ).

Утверждения 2), 3) и 4) теоремы 1 можно доказать аналогично, используя при этом определение производной, свойства пределов, а также связь между дифференцируемостью и непрерывностью функции.

Кратко правила дифференцирования суммы, разности, произведения и частного дифференцируемых функций можно сформулировать так:

Правило 1 (правило дифференцирования суммы двух дифференцируемых функций).

Производная суммы двух дифференцируемых функций равна сумме производных слагаемых функций, то есть

(u + v)′ = u′+ v′.

Замечание 4. Правило 1 распространяется на случай суммы любого конечного числа функций.

Правило 2 (правило дифференцирования разности двух дифференцируемых функций).

Производная разности двух дифференцируемых функций равна разности производных этих функций, то есть

(u −v)′ = u′−v′.

Правило 3 (правило дифференцирования произведения двух дифференцируемых функций).

Производная произведения двух дифференцируемых функций равна сумме произведений производной первого сомножителя на второй сомножитель и первого сомножителя на производную второго сомножителя, то есть

(u v)′ = u′v + uv′.

130

Замечание 5. Правило 3 распространяется на случай произведения любого конечного числа дифференцируемых функций. А именно, производная произведения n функций равна сумме n слагаемых, где каждое i-е слагаемое (i =1,2,L, n) есть произведение производной i-го сомножителя на ос-

тальные функции.

В частности, для произведения трех функций имеем:

(uvf )′ = u′vf + uv′f + uvf ′;

для произведения четырех функций имеем:

(uvfg )′ = u′vfg +uv′fg + uvf ′g +uvfg′.

Правило 4. Постоянный множитель можно вынести за знак производной, то есть

(c u)′ = c u′, где c = const .

Правило 5 (правило дифференцирования частного двух дифференцируемых функций).

Для отыскания производной дроби, числитель и знаменатель которой есть дифференцируемые функции, следует из произведения производной числителя на знаменатель вычесть произведение числителя на производную знаменателя и полученную разность разделить на квадрат знаменателя, то есть

u	′	′	′
	=	u v −uv		.

		v 2
v

(Естественно, рассматриваем производную дроби в тех точках, в которых знаменатель отличен от нуля).

Приведем примеры использования приведенных выше правил дифференцирования.

Пример 11. Найти производную функции y = ln x + cos x .

Решение. Данная функция представляет собой сумму двух слагаемых. Поэтому, используя правило 1 и табличные формулы (IV*) и (VI), получаем

131

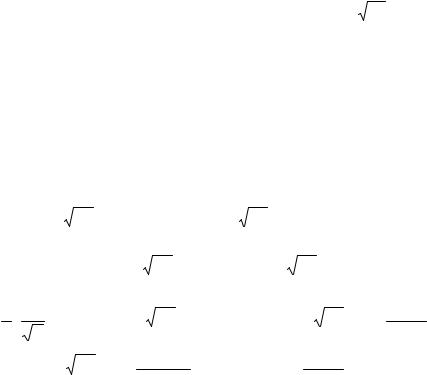
	′	′	′	′	1
y		= (ln x + cos x)	= (ln x) + (cos x) = x −sin x .

Пример 12. Найти производную функции				y = x5	−sin x .

Решение. В данном примере имеем разность двух функций. Воспользуемся правилом 2 и табличными формулами (II) и (V). Имеем

y′ = (x5 −sin x)′ = (x5 )′ − (sin x)′ = 5x 4 − cos x .

Пример 13. Вычислить производную функции y = x7 2x .

Решение. Поскольку заданная функция есть произведение двух сомножителей, то, применяя правило 3 и табличные формулы (II) и (III), находим

y′ = (x7 2x )′ = (x7 )′ 2x + x7 (2x )′ = 7x6 2 x + x7 2x ln 2 = x6 2x (7 + x ln 2).

Пример 14.

Найти производную функции f (x)= 5 tgx

в точке x = 0 .

Решение. Используя правило 4 и табличную формулу (VII), имеем:

′

tgx) = 5(tgx)

′

= 5 cos2 x = cos2 x . При x = 0 получаем:

= 1

= 5 .

f (x)= (5

(0)= cos2 0

Пример 15.

Вычислить производную функции y = 3

x 2

10x arctgx + ln 2 .

Решение. Заданная функция представляет собой сумму двух слагаемых, причем первое слагаемое есть произведение трех функций, а второе слагаемое – постоянная. Поэтому для вычисления производной данной функции применяем правило 1, замечание 5, а также табличные формулы (I), (II), (III) и (XI). В результате получаем:

y′ = (3

x 2 10x arctgx + ln 2)′

= (3 x 2 10x arctgx )′

+ (ln 2)′ =

′

(10

′

arctgx +

)

(arctgx )

10x arctgx + 3

x 2 10x

ln10 arctgx + 3

x 2 10x

+ x 2

x 2arctgx

+ ln10 arctgx

+ x 2

Пример 16. Найти производную функции

y =

ln x

132

Решение. Применяем правило 5, а также табличные формулы (II) и (IV*). Имеем:

′

3 ′

′

3x 2 ln x − x3

′

(x ) ln x − x

(ln x)

3x ln x − x

x (3ln x −1)

ln x

Пример 17. Найти производную функции

y =

x3 + 5x 2

x −5

Решение. Для отыскания производной заданной функции воспользуемся прежде всего правилом 5. Получаем:

y′ = (x3 + 5x 2 + 3)′(x −5)− (x3 + 5x 2 + 3) (x −5)′ .

(x −5)2

Затем применяем правила 1, 2 и 4 и формулы (II) и (I) таблицы производных. В результате имеем:

y′ =

(3x 2 +10x) (x −5)− (x3 + 5x 2 + 3) 1

3x3 −15x 2 +10x 2 −50x − x3 −5x 2 −3

(x −5)2

2x3

−10x2

−50x

−3

(x −5)2

Пример 18.

Вычислить производную функции

y =

x cos x

1 + 2e x

Решение. Согласно правилу 5

y′ =

(x cos x)′ (1 + 2e x )− x cos x (1 + 2e x )′

(1 + 2e x )2

Теперь воспользуемся правилами

3, 1, 4 и табличными формулами (II), (VI),

(I), (III*). В итоге получаем:

′

)− x cos x

′

+ 2(e

′

(x ) cos x + x

(cos x ) (1

(1)

)

y′ =

(1 + 2e x )2

)− 2x

(1 cos x + x (−sin x )) (1 + 2e x )− x cos x 2e x

(cos x − x sin x ) (1 + 2e x

e x cos x

(1 + 2e x )2

Пример 19. Найти производную функции y =

arcsin x

− x 2 tgx .

ln x + ctgx

Решение. Используя правило 2, можем записать

133

	arcsin x	′		2	′
y′ =			− (x		tgx) .
y′ =			− (x		tgx) .

ln x + ctgx

Применяем теперь правила 5, 3, 1 и табличные формулы (IX), (IV*), (VIII), (II), (VII). Имеем:

y′ =

(arcsin x )′ (ln x + ctgx )−arcsin x (ln x + ctgx )′

−

2 )′ tgx + x 2 (tgx )′

(ln x + ctgx )2

(ln x + ctgx )− arcsin x

−

sin 2

1 − x

(ln x + ctgx )2

− 2x tgx + x 2

cos2

ln x + ctgx

−

(sin 2 x − x ) arcsin x

x sin

1 − x

− 2x tgx −

(ln x + ctgx )2

cos2 x

Замечание 6. Пользуясь правилом 5 и табличными формулами (V) и (VI), можно получить производные функций y = tgx, y = ctgx , то есть вывести формулы (VII) и (VIII) таблицы производных основных элементарных функций. Имеем:

′

sin x ′

(sin x )′ cos x −sin x (cos x )′

cos x cos x −sin x (−sin x )

(tgx ) =

cos2 x

cos2

cos x

cos2 x + sin 2

;

cos2 x

cos2

′

cos x

′

(cos x )′

sin x − cos x (sin x )′

−sin x sin x − cos x cos x

(ctgx )

sin 2 x

sin 2

sin x

= −	sin 2	x + cos2 x	= −	1		;
		sin 2 x		sin 2
					x

Задания для самостоятельной работы

1.Найти производные следующих функций:

а)	y = 3x 2 − 2x +1;	б)	S =	2t −1	; в) y = 2 x sin x −3x cos x;	г) y =	4 − ln x	;
				2t +1			e x

д)	y = 3 x arctgx + 3	2;	е)	y = arcsin x ctgx log5 x;

2.Найти производные заданных функций в указанных точках:

а) y = (x − 4)(x 3 + x − 4), x = 0; б) y = 4 x + 1 −1, x =1;

3 x 2

134

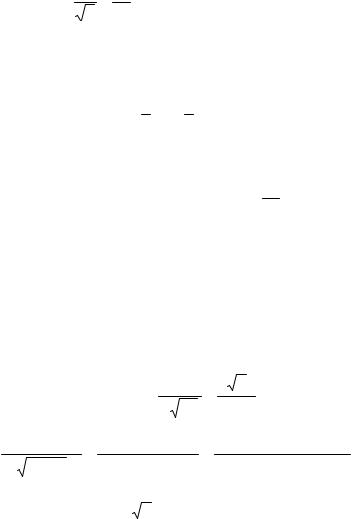
в)

г) y =

tgx

y = e

x = π;

, x = 2;

sin x + cos x

д)

y =

4x ln x

x = 4;

е) ρ =

ϕ (1 −sin ϕ)

ϕ = 0.

1 + eϕ

3.Дана функция y = 13 x3 − 52 x 2 + 6x. Найти сумму корней производной этой

функции.

4. Доказать, что для функции y = 7 + exx справедливо равенство

y′

= 7 − y.

−

e x

Ответы:

1. а)

y′ = 2 (3x −1); б)

S ′ =

; в)

y′ = 2 x (ln 2 sin x + cos x)+ 3x (sin x − ln 3 cos x);

(2t +

1)2

г) y

′

x ln x − 4x

−1

; д) y

′

arctgx

= 33 x 2

+ 1

+ x 2 ;

x e x

е) y′ = ctgx log5 x − arcsin x log5 x

+ arcsin x ctgx log5 e .

1 − x 2

sin 2 x

2. а) -8; б) −

; в) 6 2 e2 + 4; г) -1; д) 16 ln 2 2 +1; е)

3. 5.

§5. Производная обратной функции

Теорема 2. Если функция

y = f (x) определена, непрерывна, строго мо-

нотонна в некоторой окрестности точки x0 и в точке x0

имеет производную

f ′(x 0 )≠ 0 ,

то обратная к ней функция

x = g(y) имеет производную в точке

y0 = f (x0 )

, при этом

g ′(y0 )=

(2)

f ′(x0 )

Доказательство. Поскольку функция y = f (x) определена, непрерыв-

на и строго монотонна в некоторой окрестности точки x0 , то обратная функция x = g(y) определена, непрерывна и строго монотонна на некотором интервале,

содержащем точку y0 = f (x0 ) (см. теорему 31 главы I).

135

Дадим значению y0 аргумента y обратной функции x = g(y) прираще-

ние ∆y ≠ 0 . Тогда функция

x = g(y)

получит приращение ∆x , причем ∆x ≠ 0 .

При ∆x ≠ 0 и ∆y ≠ 0 имеем:

∆x

(3)

∆y

∆x

Пусть ∆y → 0 . Тогда в силу непрерывности функции x = g(y ) в точке y0

получаем, что ∆x → 0 . По условию теоремы в точке x0

существует производ-

ная функции y = f (x), то есть существует lim

∆y

= f ′(x0 )≠ 0 . Таким образом,

∆x→0

∆x

существует предел правой части равенства (3) и он равен

f ′(x0 )

А тогда существует предел и левой части этого равенства, то есть

lim

∆x

и этот предел равен

. Учитывая, что

lim

∆x = g ′(y0 ), оконча-

∆y

f ′(x0 )

∆y→0

∆y

тельно получаем:

g ′(y0 )= f ′(1x0 ).

Теорема доказана.

Замечание 7. Опуская значение аргумента и используя другое обозначение производной, формулу (2) можно записать так:

x ′y = y1′x .

Результат, полученный в теореме 2, сформулируем кратко, в виде следующего правила: производная обратной функции равна обратной величине производной прямой функции.

Правило дифференцирования обратной функции можно, в частности, использовать для получения производных обратных тригонометрических функций по известным производным функций y = sin x, y = cos x, y = tgx,

y = ctgx , то есть для установления формул IX-XII, приведенных в таблице производных основных элементарных функций. Рассмотрим, например,

136

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 3614 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.03.2016530.94 Кб91latina.doc
#
24.04.20192.01 Mб52Leblanc_Lupin_M.doc
#
20.04.2019154.82 Кб76Lektsii_po_gos_upravleniyu_i_politike.docx
#
20.09.2019390.14 Кб248lexicologie.doc
#
10.02.20154.22 Mб643Lysikova_O_V_Muzei_mira_Uchebnoe_posobie_-_M.pdf
#
10.02.20152.98 Mб163mat_analiz.pdf
#
25.09.20191.02 Mб53mat_logika.doc
#
10.02.2015273.41 Кб64METODIChESKIE_REKOMENDATsII_Yudenko.doc
#
14.11.2019274.43 Кб46METODIChESKIE_REKOMENDATsII_Yudenko.doc
#
23.08.201959.08 Кб4metodich_ukaz_k_kurs_rabotam_osn_biznesa.docx
#
10.02.201562.65 Кб22metodika_obuchenia_istorii.docx