Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Красноярский государственный педагогический университет им. В.П. Астафьева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

mat_analiz

.pdf

Скачиваний:

163

Добавлен:

10.02.2015

Размер:

2.98 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 365 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

в) если k ≠ 0 , а b = 0 , то функция имеет вид y = kx и называется пря-

мой пропорциональностью, а коэффициент k – коэффициентом пропорцио-

нальности.
Пусть x0 принадлежит области определения функции	y = f (x). Если
значение аргумента функции изменится от x0 до значения x	на величину
∆x = x − x0 , то значение функции изменится соответственно	от значения

y0 = f (x0 ) до значения y = f (x); тоестьнавеличину ∆ y = f (x)− f (x0 ) (см. рис. 17). Величину ∆x называют приращением аргумента, а ∆y - приращением функции, соответствующим приращению ∆x аргумента. Заметим, что «приращение» может быть как положительным, так и отрицательным или равным

нулю.	Вычислим ∆y для линейной функции y = kx + b (k ≠ 0):
	∆y = f (x)− f (x0 )= (kx + b)−(kx0 + b)= k(x − x0 )= k ∆x,
то есть	∆y = k ∆x.. А это означает, что приращение линейной функции прямо

пропорционально приращению аргумента.

2. Квадратичная функция

Квадратичная функция имеет общий вид

y = ax2 + bx + c,

где a, b, c – действительные числа, причём a ≠ 0 . Если a = 0 , то квадратный

трёхчлен превращается в линейный двучлен. Квадратичная функция определена на множестве всех действительных чисел (− ∞; + ∞). Графиком функции является парабола, ось симметрии которой параллельна оси Oy при b ≠ 0 или

совпадает с осью Oy при b = 0 , уравнение оси симметрии есть x = −							b	.
								.
							2a
		b		b	2
	−	b	; c −	b

Вершина параболы имеет координаты		2a		4a		.
		2a		4a

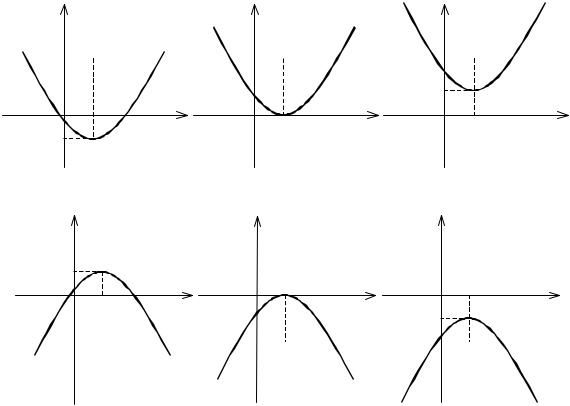
Если a > 0 , то ветви параболы направлены вверх, то есть в положительном направлении оси Oy , а квадратичная функция убывает на промежут-

				b				b	2
ке	− ∞; −					до значения	c −			и неограниченно возрастает на промежутке
ке	− ∞; −					до значения	c −	4a		и неограниченно возрастает на промежутке
			2a					4a
	b				(см. рис. 18).
−		; + ∞
−	2a	; + ∞
	2a
		Если				a < 0 , то ветви параболы направлены вниз, то есть в отрицатель-

ном направлении оси Oy , и квадратичная функция возрастает на промежутке

− ∞; −

до значения

c −

и неограниченно убывает на промежутке

(см. рис. 19).

−

; + ∞

а)

a>0

б)

y a>0

в)

a>0

− b

c −

b2 0

0 − b

Рис. 18

а)

a<0

б)

a<0

в)

a<0

c −

− b

0 − b

c −

Рис. 19

Значение функции равно нулю при значениях аргумента, которые являются корнями квадратного уравнения

ax2 + bx + c = 0.

Если дискриминант уравнения D = b2 − 4ac положительный, то уравнение имеет два действительных корня, а парабола имеет две точки пересечения с осью Ox (см. рис. 18 а, 19 а).

Если дискриминантD = 0 , то уравнение имеет один действительный корень, а парабола касается оси Ox (см. рис. 18 б, 19 б).

Если дискриминантD < 0 , то квадратное уравнение не имеет действительных корней, квадратичная функция в ноль никогда не обращается, а ее график не пересекает ось Ox , он расположен выше оси Ox при a > 0 и ниже оси Ox при a < 0 (см. рис. 18 в и 19 в).

3. Степенные функции

Для любого действительного числа α функция y = xα называется сте-

пенной функцией с показателем степени α . Рассмотрим некоторые из степенных функций.

а) Степенная функция с натуральным показателем степени α = n :

y = xn , n N.

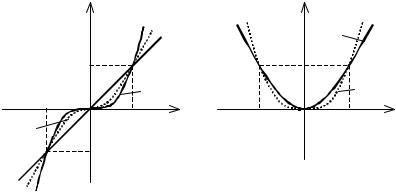
Функция определена на множестве всех действительных чисел и непрерывна там. Если n нечётное число, то функция y = xn является нечётной,

возрастающей и принимает значения от − ∞	до	+ ∞ (см. рис. 20 а).
Если n чётное число, то функция y = xn		является чётной, принимает
неотрицательные значения от нуля до + ∞,	убывает на промежутке (− ∞; 0] и

возрастает на промежутке [0; + ∞) (см. рис. 20 б).

а)	y		б)	y
				y=x2
	1	y=x		1
	1	y=x5		y=x4
–1		y=x5		y=x4
–1		0 1 x	–1	0 1 x
y=x3		0 1 x	–1	0 1 x
		–1

Рис. 20

б) Степенная функция с целым отрицательным показателем степени α = −n :

y = x−n , n N.

Функция определена для всех x R, кроме x = 0 , то есть область опреде-

ления функции состоит из объединения двух промежутков (− ∞; 0) (0; + ∞)и

функция непрерывна на каждом из них. Функция никогда в ноль не обращается.

Если n число нечётное, то функция y = x−n = x1n является нечётной функцией, убывающей на промежутках непрерывности (− ∞; 0) и (0; + ∞).

МножествозначенийфункцииестьмножествоY=(− ∞; 0) (0; + ∞)(см. рис. 21а).

Если n число чётное, то функция y = x−n = x1n является чётной. Функция

возрастает неограниченно на промежутке (− ∞; 0) и убывает на промежутке

(0; + ∞), приближаясь своими значениями к нулю, но никогда его не достигая.

Значения функции всегда положительные, множество значений есть множество Y= (0; + ∞) (см. рис. 21б).

а)				б)	1
					1
		y =	1		y =
y=x–n	y		1		y =		x4	y	y=x–n
y=x–n	y		x3				x4	y	y=x–n
n–нечетное			x3		1			1	n–четное
	1			y =
	1			y =		x2

		–1
		0 1 x	–1	0 1 x
		–1
y =	1
y =	x		Рис. 21
	x

в) Степенная функция с показателем степени

α =

, n N .

y = x

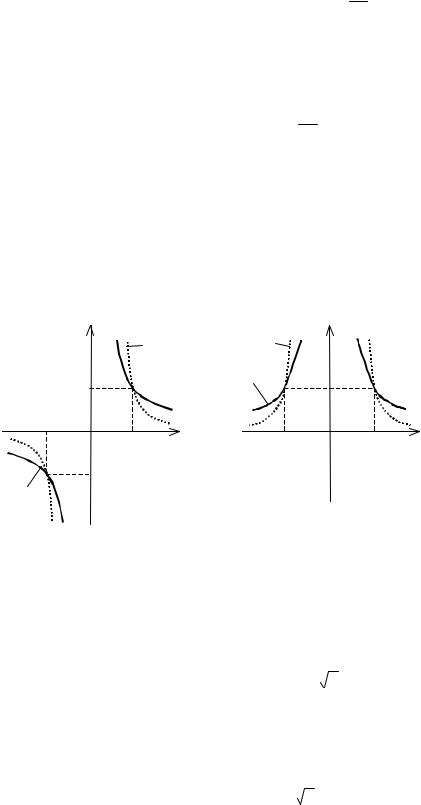
Если число n нечётное, то функция y = x

= n x

определена на множе-

стве всех действительных чисел

(− ∞; + ∞), непрерывна, является нечётной

функцией и возрастающей от − ∞

до + ∞ (см. рис. 22а).

Если число n чётное, то функция y = x

= n

определена только для не-

отрицательных значений аргумента (x ≥ 0), принимает неотрицательные зна-

чения и непрерывна в области определения и возрастает от 0 до + ∞ (см.

рис.22б).

а)	y	y = n x	б) y			y = n x
		n–нечетное	1	y =	x	n–четное
y = 3 x	1		1
y = 3 x	1	y = 5 x				y = 4 x
–1		y = 5 x				y = 4 x
–1	0	1 x		0	1	x
	0	1 x	y=x	0	1	x
	–1		y=x
	–1

y=x

Рис. 22

г) Степенная функция с рациональным показателем степени

α = ± mn ,

	m		y = x−	m
m N, n N : y = x		,			.
	n			n

В этом случае, степенную функцию можно рассмотреть как сложную:

	m		где z = xm ) и y = x−	m		1 .
y = x		= n xm (то есть y = n z ,			=
	n			n
					n	xm

4. Показательные функции.

Функцияy = a x для любого действительного числа a > 0 и a ≠1 называ-

ется показательной функцией. Показательная функция определена на множестве всех действительных чисел x (− ∞; + ∞) и принимает только положи-

тельные значения Y = (0; + ∞).. Функция непрерывна в области определения,

причем убывающая, если 0<a<1 и возрастающая, если a>1 (см. рис. 23 а, б).

а)	y			б)	y
	y		= ax		y
		y	= ax		y = ax
		0 < a <1			a >1
	1				1

–1

1 x

Рис. 23

5. Логарифмические функции

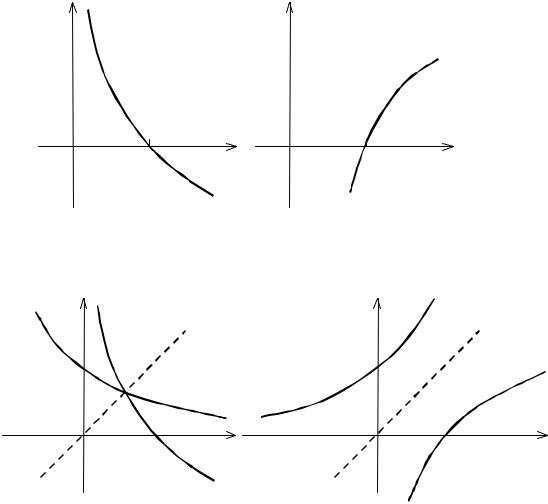
Функция обратная показательной функции называется логарифмической: y = loga x для любого a > 0 и a ≠1 . Существование логарифмической функции обуславливается строгой монотонностью показательной функции. Логарифмическая функция определена только при положительных значениях аргумента x (0; + ∞). Область значений функции есть множество всех дейст-

вительных чисел Y = (− ∞; + ∞). Если 0 < a <1 , то функция убывает, если

a >1 , то возрастает (см. рис. 24 а и б). Так как функции y = a x и y = loga x

взаимно обратные, то их графики симметричны относительно биссектрисы первого и третьего координатных углов, то есть относительно прямой y = x

(см. рис. 25 а и б).

а)		б)
y		y
	y = loga x		y = loga x
	0 < a <1		a >1

Рис. 24

y =ax

а)

y = loga

б)

0 < a <1

y = x

y =a

a >1

y = loga x

–1

Рис. 25

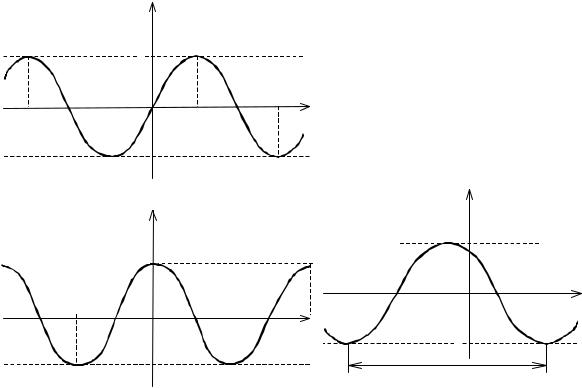
6.Тригонометрические функции

Ктригонометрическим функциям относят функции синус, косинус, тангенс, котангенс, секанс, косеканс.

а) Функции синус y = sin x и косинус y = cos x определены на множест-

ве всех действительных чисел x (− ∞; + ∞). Значения обеих функций заклю-

чены в отрезке y [−1; 1]. Функции синус и косинус непрерывны, ограничены

sin x

≤1

cos x

≤1 для

любого

x (− ∞; + ∞), периодические

с периодом

T = 2π . Синус является нечётной функцией, косинус – чётной. Синус возрас-

+ 2kπ;

достигая своего наибольше-

тает на промежутках −

+ 2kπ , k Z ,

го

значения

при

x =

π + 2kπ, k Z ,

убывает

на

промежутках

k Z , достигая своего наименьшего значения (-1) при

+ 2kπ;

π + 2kπ ,

x =

π + 2kπ,

k Z . Синус обращается в ноль при x = kπ,

k Z .

Косинус возрастает на промежутках ((2k −1)π; 2kπ ),

k Z

и убывает на

промежутках (2kπ;

(2k +1)π ), k Z . Наибольшее значение 1 косинус прини-

мает при x = 2kπ, k Z

наименьшее значение (-1) при

x = (2k −1)π, k Z , в

ноль обращается при x = π

+ kπ,

k Z . Графики функций приведены на рис.

26а и б.

б)

Для

описания

гармонических колебаний используется функ-

цияy = Asin(ωt +ϕ), где переменная

t – время, постоянные A (A > 0)- амплиту-

да,

ω (ω > 0)

– частота колебаний,

ϕ - начальная фаза, а сумма

ωt +ϕ - фаза.

Амплитуда A определяет

размах значений ординат синусоиды от − A до A ,

частота

ω определяет период колебаний T =

2π

; начальная фаза определяет

значение фазы при

t = 0 (см. рис. 27).

в)

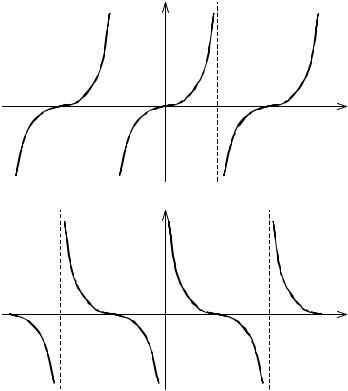
Функция тангенс

y = tg x

определена на множестве действительных

чисел, кроме x = ±	π	+ kπ,			k Z , то есть областью определения является объ-
	2
единение интервалов			−	π	+ kπ;	π
единение интервалов			−	2	+ kπ;	2	+ kπ , k Z . Функция периодическая с пе-
				2		2

риодом T = π , нечётная, возрастающая на интервалах области определения, непрерывна на них. Областью значений функции тангенс является множество всех действительных чисел Y = (− ∞, + ∞).

а)

y=sin x

−

3π

3π –π

−

–1

б)

y y=sin(ωt+ϕ)

y=cos x

A sin ϕ

–π

3π

− ω

−

− 2

–A

–1

T =

2π

Рис. 26

Рис. 27

Функция котангенс

y = ctg x

определена на множестве действитель-

ных чисел, кроме x = kπ, k Z ,

то есть на интервалах

(πk , π + kπ ),

k Z . Об-

ласть значении котангенса – все действительные числа: Y = (− ∞, + ∞). Котан-

генс –

функция нечётная, периодическая с периодом T = π , убывающая на

каждом

интервале области определения и непрерывна на нем. Как известно,

справедливы

соотношения

tg x =

sin x

ctg x =

cos x

tg x ctg x =1 .

Графики

cos x

sin x

функций y = tg x и

y = ctg x

приведены на рис. 28.

Замечание. Функции секанс

y = sec x

и косеканс

y = cos ec x определяют

следующим образом sec x =	1	; cos ec x =	1	.
	cos x		sin x

а)	y=tg x	y

–π −	π	0 π	π	x
	2	2
б)		y
y=сtg x		y

–π −	π	0	π	π	x
	2		2

Рис. 28

7. Обратные тригонометрические функции

Обратными тригонометрическими функциями являются: арксинус,

арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс.

а) Функция арксинус y = arcsin x .

Арксинусом числа x называют угол y выраженный в радианах, принад-

лежащий отрезку − π

, π

, синус которого равен

x, то есть sin y = x . Таким

образом,

арксинус

определен

на отрезке [−1; 1],

имеет область

значений

Арксинус

нечётная

функция, ограниченная

arcsin x

≤

, возрас-

−

тающая в области определения (см. рис. 29 а). Арксинус является обратной функцией к функции синус, но не на всей области определения синуса, а

только на отрезке −	π	,	π		. На этом отрезке синус является монотонной
	2		2

функцией, так что разным значениям аргумента соответствуют разные значения синуса, а это есть необходимое и достаточное условие существования обратной функции. Графики y = arcsin x, y = sin x симметричны относительно

<<< < Предыдущая 1 2 3 45 / 365 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.03.2016530.94 Кб91latina.doc
#
24.04.20192.01 Mб52Leblanc_Lupin_M.doc
#
20.04.2019154.82 Кб76Lektsii_po_gos_upravleniyu_i_politike.docx
#
20.09.2019390.14 Кб248lexicologie.doc
#
10.02.20154.22 Mб643Lysikova_O_V_Muzei_mira_Uchebnoe_posobie_-_M.pdf
#
10.02.20152.98 Mб163mat_analiz.pdf
#
25.09.20191.02 Mб53mat_logika.doc
#
10.02.2015273.41 Кб64METODIChESKIE_REKOMENDATsII_Yudenko.doc
#
14.11.2019274.43 Кб46METODIChESKIE_REKOMENDATsII_Yudenko.doc
#
23.08.201959.08 Кб4metodich_ukaz_k_kurs_rabotam_osn_biznesa.docx
#
10.02.201562.65 Кб22metodika_obuchenia_istorii.docx