
mat_analiz
.pdf
Пример 16. Являются ли монотонными следующие последовательности? Определите характер монотонности. Являются ли данные последова-
тельности ограниченными: а) |
an = 4 − |
1 |
, |
n N ; б) |
an = |
(−1)n |
, n N ; |
||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
||||
в) an = (−1)n+1 +1, |
n N ; г) an |
|
= n sin |
π n |
|
, |
|
n N ? |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: а) an = 4 − |
1 |
, n N . Покажем, что последовательность {an } |
|||||||||||||||||||||
|
|
|
n |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
возрастающая, |
для чего сравним два последовательных члена n -ый и (n +1)- |
||||||||||||||||||||||||
ый: |
an = 4 − |
1 |
|
и an+1 = 4 − |
|
|
1 |
. |
|
Так |
как |
|
1 |
> |
1 |
|
для всех n N , то |
||||||||
n |
|
n |
+1 |
|
|
n +1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||||||||
4 − |
1 |
< 4 − |
1 |
|
|
, |
а это означает, что |
an |
< an+1 , |
n N , то есть с ростом номера |
|||||||||||||||
n |
n +1 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
растут значения членов последовательности, приближаясь при этом к числу
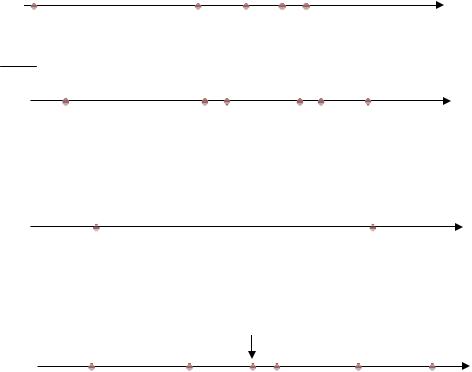
4, но не превышая его (см. рис. 36а): 3; 3 12 ; 3 23 ; 3 34 ; 3 54 ;L; 4 − 1n ,L. Последова-
тельность является ограниченной и сверху и снизу, так как 3 ≤ 4 − 1n < 4, n N .
Следовательно, она ограничена. |
В силу замечания 3 можно записать |
||||
|
an |
|
≤ 4, n N . |
(−1)n |
, n N не является монотонной, так |
|
|
||||
|
|
|
б) Последовательность an = |
||
|
|
|
n |
||
|
|
|
|
|
|
как все ее члены с чётными номерами положительные, а с нечётными номерами отрицательные. Поэтому, каждый член последовательности с нечётным номером имеет значение меньше, чем следующий за ним, а каждый член с чётным номером имеет значение больше, чем следующий за ним (см. рис. 36б):
−1, 12 , − 13 , 14 , L, (−n1)n ,L. Последовательность {an } является ограниченной, так как an = (−n1)n = 1n ≤1, n N .
в) Последовательность an = (−1)n+1 +1, n N такова, что
58
2, если n нечётное; |
(см. рис. 36в): 2, 0, 2, 0, 2, K, (−1)n+1 +1,K. Она не |
||||||
an = |
|||||||
0, если n чётное. |
|
|
|
|
|
|
|
является монотонной, но ограничена |
|
an |
|
≤ 2 . |
|||
|
|
||||||
г) Последовательность |
an = n sin |
π n |
, n N не является ограниченной и |
||||
|
|||||||
|
2 |
|
|||||
не является монотонной. Действительно, все ее члены с чётными номерами равны нулю, члены последовательности с нечётными номерами с увеличением номеров неограниченно растут по абсолютной величине:
|
|
an |
|
= |
|
nsin πn |
|
n, если n нечётное; |
Ограничить общий член |
|
an |
|
каким-нибудь |
||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
= |
если n чётное. |
|
|
|||||||
|
|
|
|
|
|
2 |
|
0, |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
одним числом для всех |
n N невозможно. Последовательность {an } является |
||||||||||||||
неограниченной |
и не |
обладает свойством монотонности (см. рис. 36г): |
|||||||||||||
1, 0, −3, 0, 5, 0, − 7, 0, 9,K, n sin |
πn |
, K. |
||||
2 |
||||||
|
|
|
|
|
||
а) |
an = 4 − |
1 |
, n N |
|
|
|
n |
|
|
||||
|
|
a1 |
|
|
||
|
|
|
|
|
||
|
|
|
3 |
|
|
|
б) an = (−n1)n , n N a1
-1
в) an = (−1)n+1 +1, n N
все an при n чётном
|
|
0 |
|
г) an = n sin |
π n |
, n N |
|
2 |
|||
|
|
|
a2 |
|
|
|
a3 |
|
|
a4 |
|
|
a5 |
|
|
|
|
|
|
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|||
3 |
|
3 |
3 |
3 |
|
|
4 |
|
|||||||||||||||||
2 |
|
|
|
3 |
|
4 |
|
5 |
|
|
|
|
|
|
|
|
|||||||||
|
|
a3 |
a5 |
|
|
|
|
|
|
|
a6 a4 |
|
a2 |
x |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
− |
|
1 |
|
− |
1 |
|
|
|
0 |
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|||||
3 |
|
5 |
|
|
|
|
|
|
|
6 |
|
|
4 |
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
все an |
при |
|
|
n нечётном |
|
|
2 |
x |
|
|
|
||
1 |
|||
an при n чётном
a |
7 |
a |
3 |
a |
a |
5 |
a9 |
|
|
|
1 |
|
|
|
|||
-7 |
|
-3 |
|
0 1 |
5 |
|
9 |
x |
Рис. 36
59

3. Предел числовой последовательности. Сходящиеся и расходящиеся последовательности
Определение 12. Число a называется пределом числовой последовательности {an }, если для любого положительного сколь угодно малого
числа ε найдется такое натуральное число N(ε), |
зависящее от ε , что для |
|||
всех номеров n ≥ N (ε) выполняется неравенство |
|
|||
|
an − a |
|
< ε |
(7) |
|
|
|||
При этом пишут an → a при n → ∞ или lim an = a . |
Неравенство (7) означает, |
|||
|
|
|
n→∞ |
|
что все члены последовательности {an } с номерами n большими N(ε), их бес-
конечно много, находятся в |
ε - окрестности точки a : a −ε < an < a +ε, n > N(ε), |
а вне ε - окрестности точки |
a находится лишь конечное число первых членов |
этой последовательности, причем их не более N(ε). |
|
|
|
Пример 17. Дана последовательность an =1 − |
1 |
, n N ; а) доказать, что |
|
n |
|||
|
|
число 1 является её пределом; б) при каких n выполняется неравенство
an −1 < 0,01?
Решение. а) Пусть ε - какое-нибудь положительное произвольно выбранное число. Выясним, с какими номерами члены последовательности
{an } попадают в |
ε - окрестность числа 1, |
для чего решим неравенство |
|
||||||||||||||||||||||||
|
an −1 |
|
< ε . |
Так |
как |
an =1 − |
1 |
, |
|
то |
последнее |
неравенство имеет |
вид |
||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
1 |
|
|
|
Отсюда |
1 |
< ε и |
n |
|
1 |
. Следовательно, все члены данной по- |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
n > |
|||||||||||||||||||||||
|
1 |
− |
n |
|
−1 |
< ε. |
|
|
|
||||||||||||||||||
|
|
|
n |
ε |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
следовательности с номерами |
n большими |
1 |
находятся в ε - окрестности |
||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
числа 1. В качестве N(ε) можно выбрать любое натуральное число больше |
|||||||||||||||||||||||||||
|
1 |
, |
например, |
N(ε)= |
1 |
+1, где |
|
|
1 |
|
|
- |
целая часть числа |
1 |
, или любое ещё |
||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
ε |
|
|
|
|
|
|
ε |
|
|
|
ε |
|
|
|
|
|
|
|
|
ε |
|
|||||
большее число. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
Таким образом, |
показано, что для любого положительного числа |
ε |
|||||||||||||||||||
найдется номер N(ε) такой, что для всех |
n > N (ε) |
справедливо неравенство |
|||||||||||||||||||||||||
60

an −1 < ε . А это означает по определению предела, что число 1 есть предел
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
данной последовательности lim 1 |
− |
|
|
|
=1. |
|
|
|
|
|
|
|
|
||||||
n |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Следует решить неравенство |
|
|
an −1 |
|
< 0,01. В данном случае ε = 0,01 . |
||||||||||||
|
|
|
|
||||||||||||||||
Тогда |
|
N(ε)= |
1 |
+1 имеет значение |
|
N(0,01)= |
1 |
|
+1 =101. Отсюда имеем, |
||||||||||
|
|
0,01 |
|||||||||||||||||
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|||
что |
все члены |
{an } с номерами |
|
|
|
n ≥101 |
удовлетворяют неравенству |
||||||||||||
|
an |
−1 |
|
< 0,01, иными словами, отличаются от своего предела не больше, чем |
|||||||||||||||
|
|
||||||||||||||||||
на 0,01. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Замечание. Ясно, что постоянная последовательность an = C, |
n N , где |
||||||||||||||||
С – константа имеет предел, и он равен С: |
lim an |
= limC = C . |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
n→∞ |
|
|||
|
|
Пример 18. Показать, что последовательность an = |
1 |
((−1)n+1 |
+1), n N |
||||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
не имеет предела. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Решение. Все члены последовательности |
{an } с нечётными номера- |
||||||||||||||||
ми равны 1 и их бесконечно много, а все члены с чётными номерами равны 0, и их тоже бесконечно много. Число 0 не является пределом данной последовательности, так как при выборе ε , удовлетворяющею условию 0 < ε <1 , вне ε - окрестности числа 0 находится бесконечное количество нечётных членов последовательности, что противоречит определению предела.
Число 1 также не является пределом данной последовательности, так как при выборе ε , удовлетворяющего условию 0 < ε <1 , вне ε - окрестности числа 1 находится бесконечное количество её чётных членов.
Рассуждая аналогичным образом, можно утверждать, что ни одно действительное число не является пределом данной последовательности. Что и требовалось доказать.
Определение 13. Если последовательность {an } имеет предел a , то её называют сходящейся и говорят, что последовательность сходится к числу a .
61

Если последовательность не является сходящейся, то её называют рас-
ходящейся.
Последовательность, рассмотренная в примере 17, является сходящейся к числу 1, а последовательность в примере 18 является расходящейся.
Теорема 2. (о единственности предела).
Всякая сходящаяся последовательность имеет только один предел. Доказательство проведем от противного. Предположим, что схо-
дящаяся последовательность {an } имеет два различных предела |
a и |
b . |
|||||||||||||||||||
Пусть для определенности |
a < b . |
Выберем число ε = |
b − a |
. Так как |
ε > 0 , то |
||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
верно неравенство a +ε < b −ε , а интервалы |
|
(a −ε, a +ε) |
и |
(b −ε, |
b +ε) |
не |
|||||||||||||||
имеют общих точек (см. рис. 37). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a −ε |
a |
a +ε |
b −ε |
|
b |
b +ε |
|
|
|
|||||||||||
|
|
|
|
|
|
|
Рис. 37 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
a = lim an , то для выбранного |
|
ε = |
b − a |
|
найдётся номер Na (ε) |
|||||||||||||||
|
|
||||||||||||||||||||
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
такой, что для всех |
номеров |
n > Na (ε) |
будет |
справедливо неравенство |
|||||||||||||||||
a −ε < an < a +ε , то есть |
an (a −ε, |
a +ε), n > Na (ε). |
|
|
|
|
|
|
|
|
|
||||||||||
Так как |
b = lim an , то для этого же числа ε = |
b − a |
найдётся номер Nb (ε) |
||||||||||||||||||
3 |
|
||||||||||||||||||||
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
такой, что для всех номеров |
n > Nb (ε) |
будет |
справедливо неравенство |
||||||||||||||||||
b −ε < an < b +ε , то есть |
an (b −ε, |
b +ε), n > Nb (ε). |
|
|
|
|
|
|
|
|
|
||||||||||
Из двух чисел Na (ε) |
и Nb (ε) выберем большее |
N(ε)= max{Na (ε), Nb (ε)}. |
|||||||||||||||||||
Тогда все члены последовательности {an } с номерами |
n > N (ε) |
принадлежат |
|||||||||||||||||||
одновременно интервалам (a −ε, a +ε) и (b −ε, b +ε) не имеющим общих то-
чек, чего быть не может.
Следовательно, предположение о существовании двух различных пределов у сходящейся последовательности неверно. Таким образом, если по-
62
следовательность сходится, то она имеет единственный предел. Что и требовалось доказать.
Определение 14. Если lim an = a и an |
≤ a, |
n N , то говорят, что после- |
||||||||||
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
довательность {an } сходится к числу a слева и пишут lim an = a − 0 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
n→∞ |
||
Определение 15. Если lim an = a и an |
≥ a, |
n > N , то говорят, что после- |
||||||||||
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
довательность {an } сходится к числу a справа и пишут |
lim an = a + 0 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
Например, последовательность |
{an }, |
где |
an =1 − |
1 |
, n N , сходится к |
|||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
числу 1 слева lim an =1 − 0 , так как an |
<1, |
n N . |
|
|
|
|||||||
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
Последовательность |
{bn }, |
bn =1 + |
1 |
, |
n N , |
тоже сходится к числу 1, но |
||||||
|
|
|||||||||||
|
|
|
|
n |
|
|
|
|
|
|
||
справа lim bn =1 + 0 , так как |
bn >1, |
n N . |
|
|
|
|
|
|
||||
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
Последовательность |
{Cn }, |
Cn =1 + |
(−1)n |
|
, n N , тоже сходится к числу 1: |
|||||||
|
|
|||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
lim Cn =1 , но члены этой последовательности приближаются к своему преде-
n→∞
лу, становясь, то больше, то меньше этого предела.
Теорема 3. (необходимый признак сходимости последовательности). Всякая сходящаяся последовательность ограничена. Доказательство. Пусть сходящаяся последовательность {an } имеет
предел a . Докажем, что она ограничена. Выберем произвольно число ε > 0 .
Тогда по определению предела найдется номер N(ε) |
такой, что для всех но- |
||||
меров n > N (ε) справедливо неравенство |
|
an − a |
|
< ε , |
то есть a −ε < an < a +ε |
|
|
||||
для n > N (ε). Вне интервала (a −ε, a +ε) |
могут оказаться лишь N(ε) первых |
||||
членов последовательности {an } : a1 , a2 ,K, aN (ε ) .
Найдем наименьшее m и наибольшее M числа среди чисел
a −ε, |
a +ε : m = min{a1 , a2 ,K, aN (ε ), a −ε, a +ε}, M = max{a1 , a2 ,K, aN (ε ), a −ε, a +ε}. |
Тогда |
m ≤ an ≤ M для всех n N . А это означает, что последовательность |
{an } ограничена (см. пункт 2 данного параграфа).
Следствие. Все неограниченные последовательности являются расходящимися.
64
Заметим, что ограниченность последовательности является необходимым, но не достаточным условием сходимости последовательности.
Например, последовательность an = (−1)n+1 , n N хотя и ограничена
0 ≤ an ≤ 2 , но предела не имеет (см. пример 16в).
Приведем без доказательства следующую теорему:
Теорема 4. (Необходимый и достаточный признак сходимости последовательности – критерий сходимости Коши).
Последовательность {an } сходится тогда и только тогда, когда для лю-
бого ε > 0 существует такой номер N (ε), |
что для всех номеров n > N (ε) и |
||||
m > N (ε) справедливо неравенство |
|
an − am |
|
|
< ε . |
|
|
||||
(Огюстен Луи Коши (21.08.1789-23.05.1857) – французский матема- |
|||||
тик). |
|
||||
4. Предел монотонной последовательности. Число e |
|||||
Теорема 5. (теорема Вейештрасса, о существовании предела монотон- |
|||||
ной последовательности).
Всякая монотонная ограниченная последовательность имеет предел. (Карл Теодор Вильгельм Вейерштрасс (31.10.1815-19.02.1897) - немец-
кий математик).
Доказательство. Пусть последовательность {an } возрастает и ог-
раничена. Требуется доказать, что она имеет предел. Условие ограниченно-
сти последовательности означает, |
что множество значений an ограничено и |
|||||
имеет верхнюю грань (см. §1, теорема 1), обозначим ее a : a = sup{an }. |
||||||
|
|
|
|
|
|
n N |
Покажем, что a = lim an . Зафиксируем произвольное число ε > 0 . Так |
||||||
|
n→∞ |
|
|
|
|
|
как a = sup{an }, то |
an ≤ a для всех |
|
|
n N , но найдется номер N (ε) такой, что |
||
n N |
|
|
|
|
|
|
a −ε < aN (ε ) . Тогда в силу возрастания последовательности |
{an } все ее члены с |
|||||
номерами n > N (ε) |
удовлетворяют неравенству a −ε < an |
≤ a . Поэтому спра- |
||||
ведливо неравенство |
|
|
|
|
||
|
|
an − a |
|
< ε , n > N (ε). |
|
|
|
|
|
|
|||
64
Итак, для произвольно выбранного числа ε > 0 , найдется номер N (ε) |
|||||
такой, что все члены последовательности {an } |
с номерами n > N (ε) удовле- |
||||
творяют неравенству |
|
an − a |
|
< ε , n > N (ε). Это |
означает по определению 12 |
|
|
||||
предела последовательности, что a = lim an , что и требовалось доказать. |
|||||
|
|
|
|
n→∞ |
|
|
Аналогичное доказательство можно провести для убывающей ограни- |
||||
ченной последовательности. |
|||||
|
Пример 19. |
(Замечательный предел). Дана последовательность {an }, |
|||
где |
|
1 |
n |
n N . Доказать, что она сходящаяся. |
|
an = 1 + |
|
, |
|||
n |
|||||
|
|
|
|
||
Решение. Покажем, что последовательность
|
|
1 |
n |
(8) |
|
an = 1 |
+ |
|
, n N K |
||
n |
|||||
|
|
|
|
возрастающая и ограниченная. Используя формулу бинома Ньютона для возведения двучлена в натуральную степень n
|
|
|
n |
|
|
|
|
|
n(n −1) 2 |
+K+ |
n(n −1) |
(n − 2)K(n |
− k +1) |
α |
k |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(1 +α) =1 + n α + 1 2 α |
|
|
|
|
|
|
|
|
|
1 2 3Kk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
+K+ |
n(n −1) (n − 2)K2 1 |
α n , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
1 2 3Kn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 n |
|
|
|
1 |
|
n (n |
− |
1) 1 |
|
|
2 |
|
|
|
n (n −1)(n − 2)K(n − k |
+1) 1 |
k |
|
|
|
|
|
|
||||||||||||||||||||||||||
a |
n |
= 1 |
+ |
|
=1 + n |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+K+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
||||||||||
|
n |
|
|
1 |
2 |
|
|
|
|
|
1 2Kk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
n (n −1)(n |
− 2)K2 1 1 |
n |
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
2 |
|
− |
k −1 |
+ |
||||||||||||||||||||||||||||||
+K+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
+ |
|
|
|
1 |
− |
|
+K+ |
|
|
|
1 |
− |
|
|
1 − |
|
|
K 1 |
|
|
|
|||||||||||||||
|
|
|
|
1 2Kn |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
1 2 |
|
|
|
1 2Kk |
|
|
n |
|
n |
|
|
|
n |
|
|||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
n −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(9) |
|
|
|||||||||||
+K+ |
|
|
|
|
|
1 |
− |
|
|
1 |
− |
|
|
K 1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 2 3Kn |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
Каждое слагаемое в формуле (9) положительное, поэтому an > 2, |
n N . |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Аналогично запишем an+1 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
65

a |
|
|
|
|
1 |
n+1 |
= |
2 + |
|
|
1 |
|
− |
|
1 |
|
|
+ |
|
|
|
|
|
|
||||||||
n+1 |
= 1 + |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
n |
+ |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
n +1 |
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
k −1 |
|
||||||
+K+ |
|
|
|
|
|
|
1 |
− |
|
|
|
|
|
1 |
− |
|
|
|
|
K 1 |
− |
|
|
|
+ |
|||||||
1 |
2 |
|
|
|
|
|
|
|
n +1 |
|
||||||||||||||||||||||
|
|
|
|
3Kk |
|
|
n +1 |
|
|
|
|
|
n +1 |
(10) |
||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
n −1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
+K+ |
|
|
|
|
|
|
1 |
− |
|
|
|
|
|
1 |
− |
|
|
|
|
K 1 |
− |
|
|
|
|
+ |
||||||
1 |
2 |
|
|
|
|
|
|
|
n +1 |
|
|
|||||||||||||||||||||
|
|
|
|
3Kn |
|
|
n +1 |
|
|
|
|
|
n +1 |
|
||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
n |
|
|||||
+ |
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
1 |
− |
|
|
|
K 1 |
− |
|
|
. |
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
n +1 |
|
|
|||||||||||||||||
|
2 3K(n +1) |
|
|
n +1 |
|
|
|
|
|
n +1 |
|
|||||||||||||||||||||
Сравним правые части формул (9) и (10). Во-первых, слагаемые в формуле (10), начиная со второго, больше соответствующих слагаемых в формуле (9), так как
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
i |
<1 − |
|
|
i |
|
|
|
, i =1, 2,K, n −1 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n + |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Во-вторых, в формуле(10) на одно положительное слагаемое больше, |
||||||||||||||||||||||||||||||||||||||||||||||||||
чем в формуле (9). Следовательно, |
|
|
|
an |
< an+1 , |
n N |
|
и доказано, что последо- |
||||||||||||||||||||||||||||||||||||||||||||
вательность {an } возрастающая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Докажем теперь, что она ограничена сверху. Заметим, что в формуле |
||||||||||||||||||||||||||||||||||||||||||||||||||
(9) |
каждая из скобок вида |
|
|
|
|
i |
|
|
для i |
=1, 2,K, n −1 меньше числа 1, и |
||||||||||||||||||||||||||||||||||||||||||
|
1 − |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
≤ |
|
1 |
|
, k N . А тогда справедливо следующее |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1 2 K k |
2k −1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
an |
< 2 + |
|
|
|
1 |
|
+ |
|
|
|
1 |
+K+ |
|
|
1 |
|
|
|
+K+ |
|
|
|
|
|
1 |
|
< 2 + |
1 |
|
+ |
1 |
|
+K+ |
1 |
|
+K+ |
1 |
= |
||||||||||||||
1 |
2 |
1 |
2 3 |
1 |
2 3Kk |
|
1 |
2 |
3Kn |
2 |
|
|
2k −1 |
2n−1 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
2n−1 |
|
1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
n N . |
Здесь |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
сумма |
||||||||||||||||||||||||||||
= 2 + 1 − |
|
|
|
|
< 3, |
|
|
|
|
+ |
|
|
|
+K+ |
|
= |
|
|
|
|
|
|
|
|
|
|
|
=1 − |
|
|
|
|||||||||||||||||||||
2k −1 |
|
2 |
|
22 |
|
2n−1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
2n−1 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
первых (n −1) членов геометрической прогрессии с первым членом и знаме-
нателем равными 12 . Таким образом, доказано, что последовательность (8)
ограничена 2 < an < 3, n N и возрастающая. В силу теоремы Вейерштрасса 5
она имеет предел. Этот предел обозначают буквой e :
66
