
- •МНОЖЕСТВА И ФУНКЦИИ. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
- •1.2 ПОНЯТИЕ ФУНКЦИИ
- •1.4 ТОПОЛОГИЯ ЧИСЛОВОЙ ПРЯМОЙ. РАСШИРЕННАЯ ЧИСЛОВАЯ ПРЯМАЯ
- •ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
- •2.1 ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
- •2.2 ЛЕММА О ВЛОЖЕННЫХ ОТРЕЗКАХ. ТЕОРЕМА ВЕЙЕРШТРАССА
- •2.3 МОНОТОННЫЕ ОГРАНИЧЕННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- •2.4 КРИТЕРИЙ КОШИ
- •ПРЕДЕЛ ФУНКЦИИ
- •3.1 ПРЕДЕЛ ФУНКЦИИ. СВОЙСТВА ПРЕДЕЛОВ ФУНКЦИИ. ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
- •3.2 КРИТЕРИЙ КОШИ СУЩЕСТВОВАНИЯ ПРЕДЕЛА ФУНКЦИИ
- •3.3 МОДИФИКАЦИЯ ПОНЯТИЯ ПРЕДЕЛА ФУНКЦИИ В ТОЧКЕ
- •3.4 ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
- •3.5 ПОРЯДОК ФУНКЦИИ. ЭКВИВАЛЕНТНОСТЬ (АСИМПТОТИКА)
- •НЕПРЕРЫВНЫЕ ФУНКЦИИ
- •4.2 ТОЧКИ РАЗРЫВА
- •4.3 СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
- •4.4 РАВНОМЕРНАЯ НЕПРЕРЫВНОСТЬ. ПРОДОЛЖЕНИЕ ПО НЕПРЕРЫВНОСТИ
- •4.5 НЕПРЕРЫВНОСТЬ ОБРАТНОЙ ФУНКЦИИ
- •4.6 ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ. ЛОГАРИФМИЧЕСКАЯ, СТЕПЕННАЯ, ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
- •ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- •5.2 ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
- •5.3 ТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ
- •5.5 ОСНОВНЫЕ ТЕОРЕМЫ
- •5.6 ПРАВИЛО ЛОПИТАЛЯ
- •5.7 ФОРМУЛА ТЕЙЛОРА
- •5.8 ФОРМУЛА ТЕЙЛОРА ДЛЯ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- •5.9 ЛОКАЛЬНАЯ ФОРМУЛА ТЕЙЛОРА
- •5.10 РЯД ТЕЙЛОРА
- •ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- •6.3 ОТЫСКАНИЕ ПЕРВООБРАЗНЫХ ДЛЯ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- •ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- •7.2 ВЕРХНИЕ И НИЖНИЕ ИНТЕГРАЛЬНЫЕ СУММЫ
- •7.3 НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ ИНТЕГРИРУЕМОСТИ ФУНКЦИИ ПО РИМАНУ
- •7.4 НЕКОТОРЫЕ КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ
- •7.5 ОСНОВНЫЕ СВОЙСТВА ИНТЕГРАЛА РИМАНА
- •7.6 СВОЙСТВА ИНТЕГРАЛА РИМАНА, В КОТОРЫХ ФИГУРИРУЮТ НЕРАВЕНСТВА
- •7.7 ИНТЕГРАЛ КАК ФУНКЦИЯ ВЕРХНЕГО ПРЕДЕЛА
- •7.8 ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА
- •7.9 ОБЩИЕ ПРИЕМЫ ИНТЕГРИРОВАНИЯ
- •7.10 НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА РИМАНА
- •НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- •8.2 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ОТ НЕОТРИЦАТЕЛЬНЫХ ФУНКЦИЙ
- •8.3 ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
- •8.4 НЕСОБСТВЕННЫЙ ИНТЕГРАЛ И РЯД

Глава 3 ПРЕДЕЛ ФУНКЦИИ
§3.1 Предел функции. Свойства пределов функции. Первый замечательный предел.
§3.2 Критерий Коши существования предела функции.
§3.3 Модификация понятия предела функции в точке.
§3.4 Второй замечательный предел.
§3.5 Порядок функции. Эквивалентность. Асимптотика.
§3.1 ПРЕДЕЛ ФУНКЦИИ. СВОЙСТВА ПРЕДЕЛОВ ФУНКЦИИ. ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
Пусть f – некоторая числовая функция, определенная на множестве E.
Определений 1. Число называется пределом функции f в точке a, если:
1. a – предельная точка множества E. |
|
2. Для любой последовательности (xn) такой, что xn |
2 E; |
xn 6= a : xn ! a ) f(xn) ! . |
( ) |
Обозначение: = lim f(x) или f(x) ! при x |
! a. |
x!a
Подчеркнем, что понятие предела функции в точке a вводится только для предельных точек a области определения функции. Отметим, что при этом функция может быть и не определена в точке a, т. е., вообще говоря, a 2= E.
Замечание 1. Условие 1 в определении предела функции в точке можно заменить следующим: функция определена в некоторой окрестности точки a, за исключением, может быть, самой точки a. Тогда мы получим определение, подпадающее под определение 1.
Замечание 2. Число = lim f(x) ничего не говорит о
x!a
значении f в точке a. Функция f(x) может быть и не определена в точке a. Утверждение lim f(x) = говорит о том, что если
x!a
37

x приближается к a, по любому закону оставаясь не равным a, то соответствующее значение f, в свою очередь, приближается к , т. е. делается сколь угодно близким к .
Определение 2. Число называется пределом функции f в точке , если:
1. – предельная точка множества E.
2. 8" > 0 9 > 0 8x 2 E x 2 (a ; a + ); x 6= a
(jf(x) j < "). ( )
Замечание. Определения 1 и 2 эквивалентны. Доказательство. Эквивалентность определений будет
доказана, если мы докажем эквивалентность условий ( ) и ( ). Доказательство будем вести от противного. Пусть справедливо ( ), но при этом не выполняется ( ). Это значит, что существует хотя бы одно " > 0 (обозначим его "0), такое, что для любого > 0 существует x 2 (a ; a + ) TE; x 6= a, для которого jf(x) j "0. Возьмем в качестве все числа вида = 1=k; k = 1; 2; 3; : : : ; и для каждого из них найдем xk 2 E, для которого
0 < jxk aj < 1=k; xk 6= a; и
jf(xk) j "0; k = 1; 2; 3; : : :
Из этих соотношений видно, что существует последовательность (xk) такая, что xk ! a (xk 6= a), в то время как f(xk) заведомо не стремится к . Таким образом, допущение, что выполняется ( ), но не выполняется ( ), приводит к противоречию.
Докажем, что из условия ( ) следует условие ( ). Пусть
справедливо ( ) и пусть задана (xn); xn 2 E : xn ! a (xn 6= a). |
||||||||||||||||
Подберем натуральное число N так, чтобы jxn aj < |
для |
|||||||||||||||
любых n > N. Тогда, согласно условию ( ), jf(xn) j < " для |
||||||||||||||||
любых n > N, т. е. f(xn) ! . Доказанное верно для любой |
||||||||||||||||
последовательности (xn), сходящейся к a (лишь бы xn 6= a), |
||||||||||||||||
поэтому из ( ) ) ( ). |
= |
cos a, |
так как j cos x cos aj |
= |
||||||||||||
|
|
Пример. x!a |
||||||||||||||
|
j |
|
|
|
lim cos x |
|
|
j |
|
j |
|
|
|
j (здесь мы использовали |
||
|
2 |
2 |
j j |
2 |
|
|
|
|||||||||
= |
|
2 sin |
x a |
sin |
x+a |
|
2 |
x a |
|
= |
|
x |
|
a |
|
|
|
|
|
|
|
|
|
|
|||||||||
неравенство j sin xj jxj; x 2 R).
СВОЙСТВА ПРЕДЕЛОВ ФУНКЦИИ
38

Теорема 1. Если f(x) определена в некоторой окрестности
точки a, за исключением, может быть, самой этой точки a и lim f(x) = , где – конечное число, то существует U(a) такая,
x!a
что ограничена в . f(x) U(a)
Доказательство. Так как lim f(x) = , то для " = 1
x!a
существует > 0 такое, что если 0 < jx aj < , то jf(x) j < 1. Таким образом, для некоторой проколотой окрестности точки
a справедливы |
неравенства jf(x)j j j jf(x) j < 1. |
|
Следовательно jf(x)j < j j + 1 для x из некоторой U(a). |
||
x Теорема 2. |
|
|
Если f(x) определена в некоторой окрестности |
||
точки a, за исключением, может быть, самой этой точки a и lim f(x) = и 6= 0, то существует U(a) такая, что jf(x)j >
x!a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j j |
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
; x 2 U(a). Больше того, для указанных x |
|
|
|
|
|
||||||
2 |
|
|
|
|
|
||||||||
|
|
f(x) > |
|
; если > 0; |
|
|
|
|
|
||||
и |
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
; если < 0: |
|
|
|
|
|
||
|
|
f(x) < |
|
|
|
|
|
||||||
|
|
2 |
" = j j |
> 0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
lim f(x) = = 0 |
|
|
||||||||
|
|
Доказательство. |
x |
|
a |
|
6 . |
Пусть |
|
|
|
|
. |
|
|
! |
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
что 8 x |
2 |
|
|
|
: |
|
Следовательно, существует |
U(a) такая, |
U(a) |
|||||||||||
jf(x) j < j2j: ) j j jf(x)j j f(x)j < j2j: ) jf(x)j >
|
j j |
|
8 |
|
2 |
|
. |
Таким образом, если > 0, то f(x) > |
|
, и |
|||
> |
2 |
; |
x |
U(a) |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
если < 0, то f(x) < |
2 . |
и g(x) |
|||||||||||
|
|
Теорема 3 (арифметические свойства). Пусть f(x) |
|||||||||||
определены в некоторой окрестности точки a, за исключением, может быть, самой точки a. Тогда справедливы равенства:
lim(f(x) |
|
g(x)) = lim f(x) |
lim g(x); |
|
|
||
x!a |
x!a |
|
x!a |
|
|
||
lim f(x) |
|
g(x) = lim f(x) |
|
lim g(x); |
( |
) |
|
x!a |
|
x!a |
x!a |
|
|
||
lim f(x) =
x!a g(x)
lim f(x)
x!a |
|
(lim g(x) = 0); |
||
lim g(x); |
||||
x!a |
6 |
|||
x!a
в том смысле, что если определены правые части, то определены левые, и они равны.
39
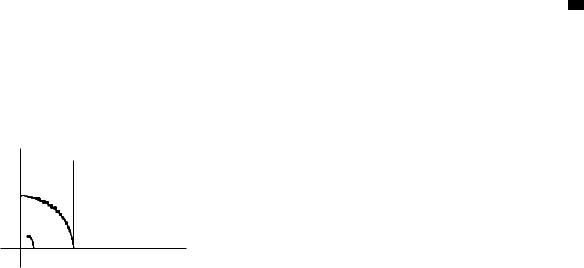
|
|
Доказательство. Пусть определены правые части равенств |
|||||||||||||||||||||
( ), т. е. |
|
lim f(x) = |
и |
lim g(x) = |
. Пусть |
x |
|
! |
a (x |
|
= a; |
||||||||||||
x!a |
x!a |
|
|
|
|
n |
|
n |
6 |
|
|||||||||||||
n = 1; 2; : : :), тогда lim f(xn) = ; lim g(xn) = . Но для числовых |
|||||||||||||||||||||||
последовательностей равенства (*) верны, т. е. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
lim(f(xn) g(xn)) = lim f(xn) lim g(xn); |
|
|
|
|
|||||||||||||||
|
|
|
|
lim f(xn) g(xn) = lim f(xn) lim g(xn); |
|
|
( ) |
||||||||||||||||
|
|
|
|
f(xn) |
|
|
lim f(xn) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
lim |
|
|
= |
|
|
; (lim g(xn) 6= 0): |
|
|
|
|
|
||||||||
(Условие |
|
g(xn) |
lim g(xn) |
a |
|
|
6 |
|
|||||||||||||||
|
lim g(xn) 6 |
0 |
|
выполняется, так как |
x |
|
|
|
|||||||||||||||
g(x |
|
) = 0 |
= |
|
lim g(x) = 0 |
|
|
g(x |
|
|
|
lim g(x) |
|
= 0; |
|||||||||
|
, так как, если |
, то |
|
) = |
! |
|
|
|
|
||||||||||||||
|
n |
6 |
|
x a |
6 |
|
n |
6 |
0 в некоторой |
||||||||||||||
окрестности точки a). Так!как равенства ( ) выполняются для |
|||||||||||||||||||||||
любой последовательности xn ! a; xn |
6= a, то равенства ( ) |
||||||||||||||||||||||
справедливы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
|||||||||
|
|
Теорема 4. ("Свойство двух милиционеров"). |
|
|
|||||||||||||||||||
f1(x); f2(x); '(x) определены |
в |
|
некоторой |
|
окрестности |
||||||||||||||||||
точки a, за исключением, может быть, самой точки a, и |
|||||||||||||||||||||||
удовлетворяют неравенствам f1(x) '(x) |
f2(x). Пусть |
||||||||||||||||||||||
lim f1(x) = lim f2(x) = . Тогда lim '(x) = . |
|
|
|
|
|
|
|
|
|||||||||||||||
x!a |
|
|
x!a |
|
|
|
x!a |
|
|
|
|
6= |
a; |
тогда |
при |
||||||||
|
|
Доказательство. Пусть xn |
! a; |
xn |
|
||||||||||||||||||
достаточно большом N для n > N f1(xn) '(xn) f2(xn). |
|
Далее, так как lim f1(x) = ; lim f2(x) = , то lim f1(xn) = и |
|
x!a |
x!a |
lim f2(xn) = и по "Свойству двух милиционеров" для числовых последовательностей существет lim '(xn) = . В силу того, что (x ) является произвольной последовательностью, сходящейся
к n, утверждение теоремы доказано. x a
ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
lim sin x |
= 1. |
|
|
x!a |
x |
|
|
Доказательство. |
|
||
y 6 |
|
N |
|
|
|
||
|
|
|
|
|
A |
|
|
|
|
|
|
|
T |
|
|
|
T |
|
|
x TTM |
- |
||
0 |
|
|
x |
40
