§ 7.9 ОБЩИЕ ПРИЕМЫ ИНТЕГРИРОВАНИЯ

§ 7.10 НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА РИМАНА

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

kniga1.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

1.54 Mб

Скачать

☆

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2526 / 2926 27 28 29 > Следующая >>>

10. (Формула интегрирования по частям). Пусть f и g – непрерывные кусочно-гладкие на [a; b] функции. Тогда

b		b
Za	f(x)g0(x)dx = f(x)g(x)jab Za	f0(x)g(x)dx:

Доказательство. f(x); g(x) – непрерывные кусочно-гладкие

на [a; b] функции.) f(x) g(x) – непрерывная кусочно-гладкая на [a; b] функция.) f(x) g(x) имеет на [a; b], за исключением конечного числа точек, непрерывную производную (f(x)g(x))0 = f(x)g0(x) + f0(x)g(x). По обобщенной формуле НьютонаЛейбница, имеем

Z	b
	b

(f(x)g(x))0dx = f(x)g(x) :


a			a
a
Отсюда следует
	b	b
	b	= Z (f(x)g0(x) + f0(x)g(x))dx =
f(x)g(x) a		= Z (f(x)g0(x) + f0(x)g(x))dx =
		a

b			b
= Za	f(x)g0(x)dx + Za		f0(x)g(x)dx:	(1)

Заметим, что функции f(x)g0(x); f0(x)g(x) – интегрируемы на [a; b], так как f и g являются, по условию, непрерывными кусочно-гладкими на [a; b] функциями. Из (1) следует требуемое равенство:

	b	b	b
		b
Z		f(x)g0(x)dx = f(x)g(x) a	Z	f0(x)g(x)dx:


a			a

149

	20. (Формула замены переменной). Пусть f : [a; b]		! R
		кусочно-гладкая на
непрерывная, а ' – непрерывная			[c; d]

функция, причем '(c) = a, '(d) = b и определена суперпозиция

f '. Тогда	b	d
	Z	Z

f(x)dx = f('(t))'0(t)dt:

Доказательство. Пусть F (x) – первообразная функции f и разбиение c = t0 < t1 < : : : < tn = d такое, что '(t) – гладкая

на каждом отрезке [ti 1; ti]. Тогда dtd F ('(t)) = f('(t))'0(t); t 2 (ti 1; ti), и, следовательно,

Z	b				n
					n
	f(x)dx = F (b) F (a) = F ('(d)) F ('(c)) = i=1 [F ('(ti))
a					X
		n	ti	d
		n	Z	f('(t))'0(t)dt = Z
	F ('(ti 1))] =	i=1			f('(t))'0(t)dt:
					f('(t))'0(t)dt:

		Xti 1		c

f( i) 1 + f0( i)2(xi xi 1 +

xI. Формула Тейлора с остатком в интегральной форме.

Пусть f : ( ; ) ! R; < a < и f(n) – непрерывна на отрезке [a; x] ( ; ) (или [x; a] ( ; )). Тогда

n 1

f(k)(a)(x a)k +

f(n)(t)(x t)n 1dt: ( )

f(x) = k=0

1)!

(Величина

rn(x)

f(n)(t)(x

t)n 1dt

называется

1)!

остатком в интегральной форме)R .

Доказательство. Мы имеем: f(x)

f(a) =

f0(t)dt =

tf0(t)

xf0(x)

f00(t)tdt

af0(a)

+ xf0(a)

xf0(a)

150

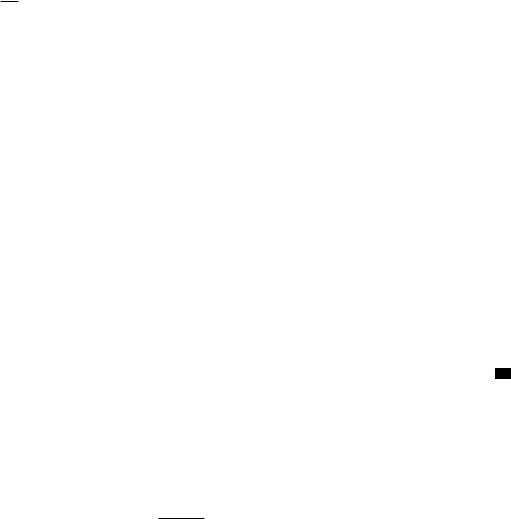
x	x	x
Ra	f00(t)tdt = f0(a)(x a) + x Ra	f00(t)dt Ra	f00(t)tdt = f0(a)(x

a) + R f00(t)(x t)dt. Таким образом, формула ( ) справедлива

для n = 1; 2. Пусть она справедлива для всех k n 1. Тогда

n 2

f(x) = X k1!f(k)

k=0

(a)(x a)k +	1

	(n 2)!

f(n 1)(t)(x t)n 2dt: (2)

Интегрируя по частям интеграл в правой части, имеем:

x				x
				x
Zf(n 1)(t)(x t)n 2dt=		1		f(n 1)(t)(x t)n 1 a+
Zf(n 1)(t)(x t)n 2dt=	n		1	f(n 1)(t)(x t)n 1 a+
a

(x t)n 1f(n)(t)dt=

f(n 1)(a)(x a)n 1 +

f(n)(t)(x t)n 1dt: (3)

Из (2) и (3) следует формула ( ).

Замечание. Используя интегральную форму остаточного члена формулы Тейлора, легко получить остаточный член формулы Тейлора в форме Лагранжа.

Действительно, используя теорему о среднем, получим

	x	f(n)(t) (x t)n 1dt =
(n 1)! Ra		f(n)(t) (x t)n 1dt =
1

f(n)( )

(n 1)!

x				x
x	(x t)	dt = (n 1)! n		a=
a	(x t)	dt = (n 1)! n		a=
R	n 1		f(n)( ) (x t)n


	f	(n)
	f	( )	(x a)n, где = a + (x a); 0 < < 1. Полученное
		n!	(x a)n, где = a + (x a); 0 < < 1. Полученное
выражение и представляет собой остаточный член в форме
Лагранжа.				x

II. Геометрические приложения.

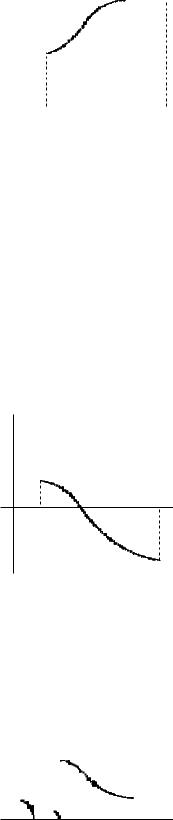
10 (Площадь криволинейной трапеции).

Рассмотрим криволинейную трапецию, т. е. фигуру типа изображенной на рис. 1.

151


y	6	y = f(x)
y














	S




	-			x
0	a	Рис. 1	b	x
		Рис. 1

Мы уже видели (см. § 7.1), что площадь S данной фигуры равна

S = Z	b
S = Z	f(x)dx:	( 1)
a

Замечание. При формальном использовании формулы ( 1) для площади может получиться отрицательное значение (см. рис. 2).

y
6
	y = f(x)

+
				-
			g	-
0 a g			g
0 a g		b x




	Рис. 2

20 (Площадь плоской фигуры в полярной системе координат).

Рассмотрим фигуру, ограниченную двумя выходящими из полярного полюса 0 лучами = ; = и кривой, заданной в полярных координатах непрерывной функцией r = r( ); << (см. рис. 3).

		r = r( )



			(

	((((		-	Рис. 3
(((((
0			x

152

Площадь S данной фигуры может быть определена следующим образом (см. рис. 4). Произведем разбиение отрезка [ ; ] изменения : ( = 0 < 1 < : : : < n = ).

		q
n		qp
n		n
			n 1
			3
q 2 2
p							1
p					((
	((		((						1
	((			q		q			1	-
((((						q		q		-
0		Рис. 4								x
										x

Элемент площади фигуры, ограниченной кривой r = r( ) и лучами = k 1; = k, приближенно выражаем площадью кругового сектора, ограниченного теми же лучами и окружностью радиуса rk = r( k) ( k 2 ( k; k 1)), равной

12r2( k)( k k 1). По определению полагаем

S = lim X 1r2( k) k;

d( )!0 1 2

где k = k k 1.

Так как r = r( ) непрерывна на отрезке [ ; ] изменения , то


S =	1	Z	r2( )d :	( 2)
	2

30 (Длина плоской кривой).

Длиной l кривой естественно назвать предел длин ломаных, вписанных в кривую, когда набольшее расстояние между соседними узлами ломаной стремится к 0. Пусть – график непрерывной кусочно-гладкой функции y = f(x); x 2 [a; b]. Каждая вписанная ломаная характеризуется некоторым разбиением (a = x0 < x1 < : : : < xn = b), так что длина i-того

звена li = p(xi xi 1)2 + (f(xi) f(xi 1))2 (см. рис. 5).

y = f(x)

f(xi)

f(xi 1)

Рис. 5

xi 1 xi

b x

153

Введем

функцию

(x)

1 + f0(x)2;

[a; b],

имеющую

на

[a; b]

не

более

конечного

числа

точек

разрыва.

По

Лагранжа

формуле

конечных

приращений

i(xi

1i.

l =i 1

lim

ili

px1i

1))(x0 i

i 1 xi

1);i0 <i 1

)

l =

+ (f (x

+ (x

)))2

d( ) 0 i=1

(x!

x p)

[a; b]:

lim

1 + f0( i)2(xi

1) =

lim

S (

); i

d( ) 0 i=1

1 .

d( ) 0

–

– непрерывная кусочно-гладкая на

)

интегрируема на [a; b]: )

1 + (f0)2 – интегрируема на

) d( )

существует p

)

[a; b]:

lim

(

)

при

l =	(x)dx =	1 + f0(x)2dx:	( 3)
	a	a
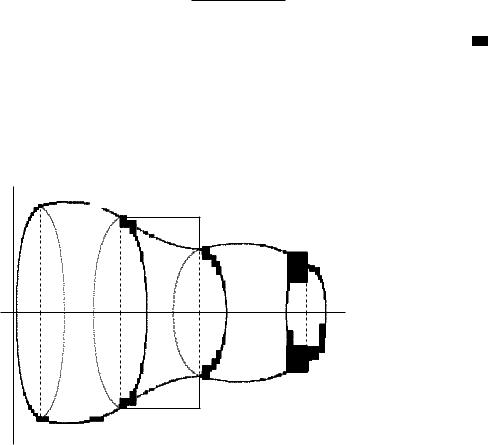
x 40 (Площадь поверхностного тела вращения).			кусочно-
Пусть y =	f(x) (x 2	[a; b]) – непрерывная	кусочно-

гладкая функция (для определенности пусть f(x) 0). Найдем– площадь поверхности, полученной вращением графика (функции f) вокруг оси 0X (см. рис. 6).

(xi; f(xi))

xi 1

Рис. 6

Пусть (a = x0 < x1 < : : : < xn = b) – разбиение [a; b]. Заменим на ломаную с узлами в точках (xi; f(xi)). Площадь

аппроксимируется площадью поверхности, возникающей при вращении ломаной. Часть поверхности вращения ломаной,

154

заключенной между узлами (xi 1; f(xi 1)); (xi; f(xi)), есть боковая поверхность усеченного конуса, и ее площадь i равна

i = (f(xi) + f(xi 1)) (xi xi 1)2 + (f(xi) f(xi 1))2 =

= (f(xi) + f(xi 1)) 1 + f0( i)2 (xi xi 1); xi 1 xi:

Отсюда искомая площадь

=lim	i =lim		(f(xi)+f(xi	1))	1 + f0( i)2 (xi	xi		1):
d( )!0 i	d( )!0	i=1
							(4)

Для вычисления преобразуем правую часть (4).

n n

+ i=1 [(f(xi) f( i)) + (f(xi 1) f( i))]q

1 + f0( i)2

(xi xi 1) :

}

есть

Сумма

P00

сумма для

функции

интегральная

2 f(x)

1 + f (x)2

Следовательно,

lim

f(x)

1 + f

(x)2dx:

d( )!0

= 2 Z

Покажем, что

00 = 0

lim

K = sup

d( )!0

. Пусть

x2[a;b] p1 + f0(x)

Тогда jf0(x)j p1 + f0(x)2 K, и применение формулы конечных приращений Лагранжа дает

[f0( i)(xi i) + f0( i)( i xi 1)] 1 + f0

( i)2

i=1

(xi xi 1)j K

(xi xi 1) K (b a)d( ):

i=1

155

Отсюда следует, что lim P00 = 0. Окончательно получаем

d( )!0

формулу площади поверхности тела вращения:

b
= 2 Z f(x)q1 + f0(x)2dx:	( 4)

50 (Объем тела по поперечным сечениям).

Рассмотрим тело, содержащееся между плоскостями x = a; x = b, и станем рассекать его плоскостями, перпендикулярными к оси 0X (см. рис. 7).

y	6	S(xi 1)
		S(xi 1)












				x
		x		x	i	-

			i 1
0	a				b	x
0	a				b	x

Рис. 7

Допустим, что все эти сечения имеют площадь, и пусть площадь сечения, отвечающего абсциссе x, – обозначим ее S(x)

– будет непрерывной функцией от x; x 2 [a; b]. Вычислим объем данного тела. Произведем разбиение отрезка [a; b] : (a = x0 < x1 < : : : < xn = b). Элемент Vi объема тела, ограниченного плоскостями x = xi 1; x = xi, приближенно равен объему цилиндра высоты xi = xi xi 1 с площадью основания

S(xi 1) :

Vi S(xi 1) xi:

Величина P Vi V и является интегральной суммой

i=1

функции S(x), которая, в силу своей непрерывности, является интегрируемой на [a; b].

156

Таким образом,

n	b
n	S(xi 1) xi = Z
V = d( )!0 i=1		S(x)dx:	(	5)


X	a
lim

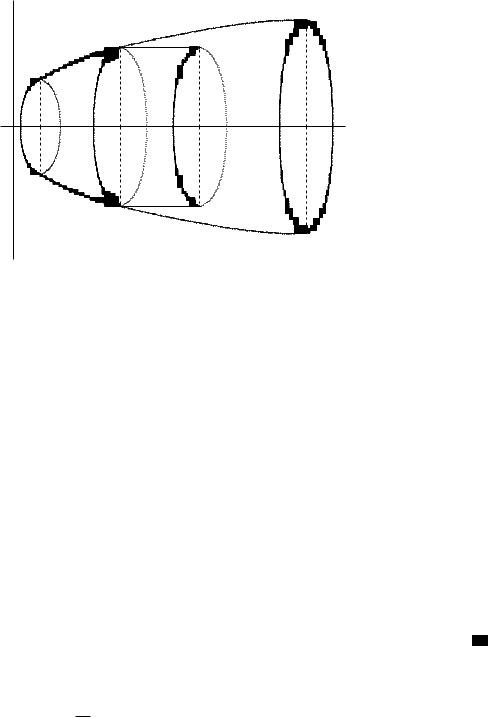
60 (Объем тела вращения).

Рассмотрим тело, ограниченное плоскостями x = a; x = b и поверхностью вращения кривой вокруг оси 0X (см. рис. 8).

xi 1	xi	b	-
0 a		b	x

Рис. 8

( – график функции y = f(x); x 2 [a; b], причем f(x) 0).

Вычислим объем V данного тела вращения.						на	части
Произведем разбиение				отрезка	[a; b]
a=x0	< x1	< : : : < xn=b.	Пусть	Vi –	элемент	объема V ,
ограниченный плоскостями x = xi 1; x = xi. Будем							считать,
что	Vi	приближенно	равен	объему	цилиндра		высоты
xi = xi xi 1 и радиуса yi 1 = f(xi 1) :

Vi yi2 1 xi = f2(xi 1) xi:

Отсюда следует:

		n		b
		n		Z
maxi	xi!0	i=1	f (xi 1) xi	Z	f (x)dx ( 6)
		X		a	2
V = lim			2	=	2
V = lim				=

– формула объема тела вращения. x Примеры.

1.Даны эллипс xa2 + yb2 = 1 и точка M(x; y) на нем (см. рис. 9).

157

Рис. 9 Необходимо найти площадь криволинейной трапеции BOKM. Из уравнения эллипса имеем

y = abpa2 x2:

Так что по формуле ( 1)

S = Z

a2 x2dx =

arcsin

x a2

=ab2 arcsin xa + xy2 :

2.Найдем площадь окружности радиуса R, используя формулу ( 2). Из рис. 10 видно, что изображенная на нем окружность определяется уравнением r = 2R cos ; 2



	R
0q	R

	-

Рис. 10 Поэтому, в силу ( 2), ее площадь равна


	2			2	cos 2
S = 2R2	Z	cos2 d = 4R2	Z	1 +	cos 2	d = R2:
				1 +
					2
2			0
			0

158

3.Дана парабола: y = 2xp2 . Найти длину l кривой – график данной параболы при изменении x от 0 до a. По формуле ( 3) имеем

x2 + p2+

+ p2 0

l = p Z

+ p2dx = p

2 ln(x+

0 p

a +

a2 + p2

pa2 + p2 +

4.Рассмотрим параболу y = x2; x 2 [0; 1]. Площадь поверхности вращения куска данной параболы вычисляется по формуле ( 4):

S = 2 Z x2p1 + 4x2dx:

(Полученный интеграл предлагается вычислить самостоятельно).

5.Вычислить объем V кругового конуса с радиусом основания r и высотой h (см. рис. 11).

y
6



			r

	h		-
0HH	HH		x
	HH
	HHH
	HHHH
	HHH
	HHH
	Рис. 11	H

Проведем перпендикулярно оси конуса, которая совпадает с осью x, секущую плоскость. Площадь сечения

159

S(x) = (hr x)2. По формуле ( 5) имеем

h		r		r2	x3	h	1
		r		r2	x3	h	1
V = Z	(		x)2dx =			0=		r2h:
V = Z	(	h	x)2dx =	h2	3	0=	3	r2h:
0

160

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2526 / 2926 27 28 29 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.09.2019155.65 Кб2Kitay_16-17_vv.doc
#
13.08.2019516.1 Кб68Klassichesky_lechebnyy___massazh.doc
#
17.11.2019104.45 Кб1kleiner Mann 1.doc
#
09.11.201886.53 Кб3kleiner Mann 1.doc
#
10.02.201531.71 Mб17Klientov_A_E_-_Narodnye_promysly_Istoria_Ross.pdf
#
10.02.20151.54 Mб48kniga1.pdf
#
12.09.201916.9 Mб4kniga_h-s.doc
#
18.08.2019142.85 Кб10kodeks-ESOMAR.doc
#
10.02.20156.82 Mб57Kogogin D.A .(RINEX) (Секция 1).rtf
#
22.12.2018310.51 Кб3Kollokvium.docx
#
29.08.2019253.95 Кб1kommer.doc